首页ode = y(x).diff(x, 2) - 4*y(x).diff(x,1) + 3*y(x) - x* math.exp(x)
ode_sol = sympy.dsolve(ode)
ode = y(x).diff(x, 2) - 4*y(x).diff(x,1) + 3*y(x) - x* math.exp(x) ode_sol = sympy.dsolve(ode)
时间: 2023-09-03 12:08:53 浏览: 88
ode = y(x).diff(x, 2) - 4*y(x).diff(x,1) + 3*y(x) - x* math.exp(x)
ode_sol = sympy.dsolve(ode)
The given differential equation is `ode = y(x).diff(x, 2) - 4*y(x).diff(x,1) + 3*y(x) - x* math.exp(x)`. To solve this equation, we can use the `dsolve` function from the `sympy` library.
Here is the code to solve the differential equation:
```python
import sympy
x = sympy.symbols('x')
y = sympy.Function('y')(x)
ode = y.diff(x, 2) - 4*y.diff(x,1) + 3*y - x* sympy.exp(x)
ode_sol = sympy.dsolve(ode)
print(ode_sol)
```
The `dsolve` function returns the general solution to the differential equation. You can print out `ode_sol` to see the solution.
阅读全文
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
最新推荐
本地磁盘E的文件使用查找到的
本地磁盘E的文件使用查找到的
CoreOS部署神器:configdrive_creator脚本详解
资源摘要信息:"配置驱动器(cloud-config)生成器是一个用于在部署CoreOS系统时,通过编写用户自定义项的脚本工具。这个脚本的核心功能是生成包含cloud-config文件的configdrive.iso映像文件,使得用户可以在此过程中自定义CoreOS的配置。脚本提供了一个简单的用法,允许用户通过复制、编辑和执行脚本的方式生成配置驱动器。此外,该项目还接受社区贡献,包括创建新的功能分支、提交更改以及将更改推送到远程仓库的详细说明。"
知识点:
1. CoreOS部署:CoreOS是一个轻量级、容器优化的操作系统,专门为了大规模服务器部署和集群管理而设计。它提供了一套基于Docker的解决方案来管理应用程序的容器化。
2. cloud-config:cloud-config是一种YAML格式的数据描述文件,它允许用户指定云环境中的系统配置。在CoreOS的部署过程中,cloud-config文件可以用于定制系统的启动过程,包括用户管理、系统服务管理、网络配置、文件系统挂载等。
3. 配置驱动器(ConfigDrive):这是云基础设施中使用的一种元数据服务,它允许虚拟机实例在启动时通过一个预先配置的ISO文件读取自定义的数据。对于CoreOS来说,这意味着可以在启动时应用cloud-config文件,实现自动化配置。
4. Bash脚本:configdrive_creator.sh是一个Bash脚本,它通过命令行界面接收输入,执行系统级任务。在本例中,脚本的目的是创建一个包含cloud-config的configdrive.iso文件,方便用户在CoreOS部署时使用。
5. 配置编辑:脚本中提到了用户需要编辑user_data文件以满足自己的部署需求。user_data.example文件提供了一个cloud-config的模板,用户可以根据实际需要对其中的内容进行修改。
6. 权限设置:在执行Bash脚本之前,需要赋予其执行权限。命令chmod +x configdrive_creator.sh即是赋予该脚本执行权限的操作。
7. 文件系统操作:生成的configdrive.iso文件将作为虚拟机的配置驱动器挂载使用。用户需要将生成的iso文件挂载到一个虚拟驱动器上,以便在CoreOS启动时读取其中的cloud-config内容。
8. 版本控制系统:脚本的贡献部分提到了Git的使用,Git是一个开源的分布式版本控制系统,用于跟踪源代码变更,并且能够高效地管理项目的历史记录。贡献者在提交更改之前,需要创建功能分支,并在完成后将更改推送到远程仓库。
9. 社区贡献:鼓励用户对项目做出贡献,不仅可以通过提问题、报告bug来帮助改进项目,还可以通过创建功能分支并提交代码贡献自己的新功能。这是一个开源项目典型的协作方式,旨在通过社区共同开发和维护。
在使用configdrive_creator脚本进行CoreOS配置时,用户应当具备一定的Linux操作知识、对cloud-config文件格式有所了解,并且熟悉Bash脚本的编写和执行。此外,需要了解如何使用Git进行版本控制和代码贡献,以便能够参与到项目的进一步开发中。
管理建模和仿真的文件
管理Boualem Benatallah引用此版本:布阿利姆·贝纳塔拉。管理建模和仿真。约瑟夫-傅立叶大学-格勒诺布尔第一大学,1996年。法语。NNT:电话:00345357HAL ID:电话:00345357https://theses.hal.science/tel-003453572008年12月9日提交HAL是一个多学科的开放存取档案馆,用于存放和传播科学研究论文,无论它们是否被公开。论文可以来自法国或国外的教学和研究机构,也可以来自公共或私人研究中心。L’archive ouverte pluridisciplinaire
【在线考试系统设计秘籍】:掌握文档与UML图的关键步骤
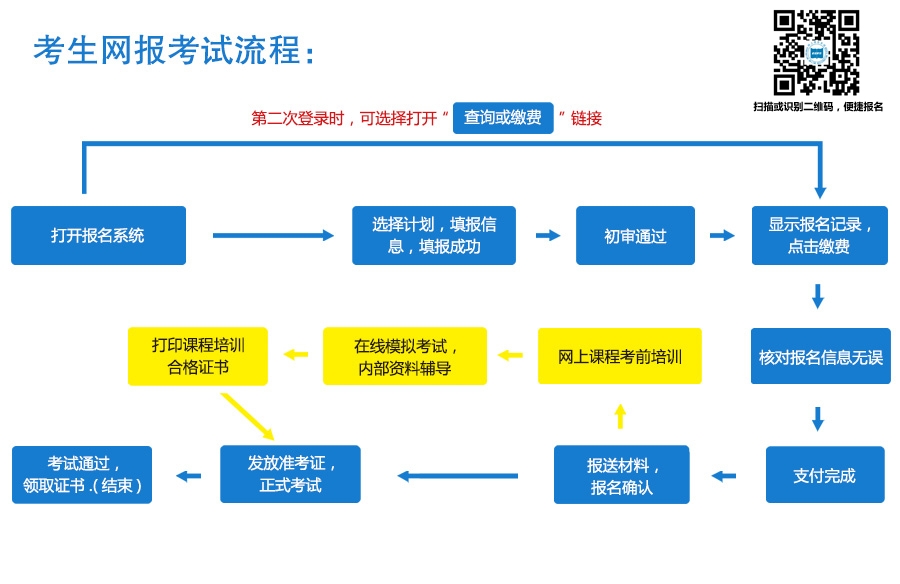
# 摘要
在线考试系统是一个集成了多种技术的复杂应用,它满足了教育和培训领域对于远程评估的需求。本文首先进行了需求分析,确保系统能够符合教育机构和学生的具体需要。接着,重点介绍了系统的功能设计,包括用户认证、角色权限管理、题库构建、随机抽题算法、自动评分及成绩反馈机制。此外,本文也探讨了界面设计原则、前端实现技术以及用户测试,以提升用户体验。数据库设计部分包括选型、表结构设计、安全性
如何在Verilog中实现一个参数化模块,并解释其在模块化设计中的作用与优势?
在Verilog中实现参数化模块是一个高级话题,这对于设计复用和模块化编程至关重要。参数化模块允许设计师在不同实例之间灵活调整参数,而无需对模块的源代码进行修改。这种设计方法是硬件描述语言(HDL)的精髓,能够显著提高设计的灵活性和可维护性。要创建一个参数化模块,首先需要在模块定义时使用`parameter`关键字来声明一个或多个参数。例如,创建一个参数化宽度的寄存器模块,可以这样定义:
参考资源链接:[Verilog经典教程:从入门到高级设计](https://wenku.csdn.net/doc/4o3wyv4nxd?spm=1055.2569.3001.10343)
```
modu
探索CCR-Studio.github.io: JavaScript的前沿实践平台
资源摘要信息:"CCR-Studio.github.io"
CCR-Studio.github.io 是一个指向GitHub平台上的CCR-Studio用户所创建的在线项目或页面的链接。GitHub是一个由程序员和开发人员广泛使用的代码托管和版本控制平台,提供了分布式版本控制和源代码管理功能。CCR-Studio很可能是该项目或页面的负责团队或个人的名称,而.github.io则是GitHub提供的一个特殊域名格式,用于托管静态网站和博客。使用.github.io作为域名的仓库在GitHub Pages上被直接识别为网站服务,这意味着CCR-Studio可以使用这个仓库来托管一个基于Web的项目,如个人博客、项目展示页或其他类型的网站。
在描述中,同样提供的是CCR-Studio.github.io的信息,但没有更多的描述性内容。不过,由于它被标记为"JavaScript",我们可以推测该网站或项目可能主要涉及JavaScript技术。JavaScript是一种广泛使用的高级编程语言,它是Web开发的核心技术之一,经常用于网页的前端开发中,提供了网页与用户的交云动性和动态内容。如果CCR-Studio.github.io确实与JavaScript相关联,它可能是一个演示项目、框架、库或与JavaScript编程实践有关的教育内容。
在提供的压缩包子文件的文件名称列表中,只有一个条目:"CCR-Studio.github.io-main"。这个文件名暗示了这是一个主仓库的压缩版本,其中包含了一个名为"main"的主分支或主文件夹。在Git版本控制中,主分支通常代表了项目最新的开发状态,开发者在此分支上工作并不断集成新功能和修复。"main"分支(也被称为"master"分支,在Git的新版本中推荐使用"main"作为默认主分支名称)是项目的主干,所有其他分支往往都会合并回这个分支,保证了项目的稳定性和向前推进。
在IT行业中,"CCR-Studio.github.io-main"可能是一个版本控制仓库的快照,包含项目源代码、配置文件、资源文件、依赖管理文件等。对于个人开发者或团队而言,这种压缩包能够帮助他们管理项目版本,快速部署网站,以及向其他开发者分发代码。它也可能是用于备份目的,确保项目的源代码和相关资源能够被安全地存储和转移。在Git仓库中,通常可以使用如git archive命令来创建当前分支的压缩包。
总体而言,CCR-Studio.github.io资源表明了一个可能以JavaScript为主题的技术项目或者展示页面,它在GitHub上托管并提供相关资源的存档压缩包。这种项目在Web开发社区中很常见,经常被用来展示个人或团队的开发能力,以及作为开源项目和代码学习的平台。
"互动学习:行动中的多样性与论文攻读经历"
多样性她- 事实上SCI NCES你的时间表ECOLEDO C Tora SC和NCESPOUR l’Ingén学习互动,互动学习以行动为中心的强化学习学会互动,互动学习,以行动为中心的强化学习计算机科学博士论文于2021年9月28日在Villeneuve d'Asq公开支持马修·瑟林评审团主席法布里斯·勒菲弗尔阿维尼翁大学教授论文指导奥利维尔·皮耶昆谷歌研究教授:智囊团论文联合主任菲利普·普雷教授,大学。里尔/CRISTAL/因里亚报告员奥利维耶·西格德索邦大学报告员卢多维奇·德诺耶教授,Facebook /索邦大学审查员越南圣迈IMT Atlantic高级讲师邀请弗洛里安·斯特鲁布博士,Deepmind对于那些及时看到自己错误的人...3谢谢你首先,我要感谢我的两位博士生导师Olivier和Philippe。奥利维尔,"站在巨人的肩膀上"这句话对你来说完全有意义了。从科学上讲,你知道在这篇论文的(许多)错误中,你是我可以依
三维点云里程碑:PointNet++模型完全解析及优化指南

# 摘要
三维点云数据是计算机视觉和机器人领域研究的热点,它能够提供丰富的空间信息。PointNet++作为一种专门处理点云数据的深度学习模型,通过其特有的分层采样策略和局部区域特征提取机制,在三维物体识别和分类任务上取得了突破性进展。本文深入探讨了PointNet++模型的理论基础、实践详解以及优化策略
华为GPON技术如何在光纤传输网络中实现数据高效传输和管理,并阐述其在业务发放和网络管理模式中的关键作用?
华为GPON技术通过其独特的光网络架构和协议,为光纤传输网络提供了高效的接入解决方案。在数据传输方面,GPON利用无源光网络的优势,通过OLT到多个ONU的光纤链路实现数据的上传和下传,大大减少了中继设备和降低了维护成本。其物理层和数据链路层协议详细规定了数据传输的细节,确保了数据的高效传输。在管理方面,华为GPON技术支持集中式和分布式管理模式,使得网络运营者能够进行远程配置和监控,实现网络的智能化管理。而DBA技术作为GPON的关键技术之一,实现了动态带宽分配,确保了网络资源的合理利用和不同业务的QoS保证。在业务发放方面,华为GPON通过支持多样化业务和个性化配置,实现了快速和高效的服务
RapidMatter:Web企业架构设计即服务应用平台
资源摘要信息: "RapidMatter是一个尝试为企业基础设施提供基于Web的企业架构设计即服务的应用程序。该应用程序的设计概念和相关文档最初位于名为/docs的目录中。"
首先,我们需要明确几个关键概念。
1. 企业架构设计:企业架构设计是指对企业中所有部分的设计和规划,以确保企业的各个组成部分能够协同工作,满足企业的业务目标。这是一个涉及到业务、数据、应用和技术各个层面的复杂过程。
2. 基础设施:在企业架构设计的语境中,基础设施通常指的是支持企业业务运行的技术基础结构,包括硬件、软件、网络设施、数据中心等。
3. 基于Web的应用程序:这是指通过互联网提供给用户的应用程序,用户可以通过浏览器访问这些应用程序,而无需在本地安装任何软件。
4. 设计即服务(Design as a Service, DaaS):这是一种服务模式,通过云平台提供设计相关的资源和工具,用户可以根据需要定制和使用这些资源,而无需自己建立和维护复杂的基础设施。
现在,我们来深入探讨RapidMatter这个项目。
RapidMatter试图通过提供一个基于Web的企业架构设计即服务应用程序,来帮助企业更好地设计和管理其基础设施。这可能包括提供设计工具、模板、最佳实践指导、自动化设计流程等功能。
从给定的信息中,我们可以推断RapidMatter可能具有以下特点和功能:
- 它允许用户通过Web界面进行企业架构设计,无需在本地安装任何专业软件。
- 它提供了一套完整的设计工具和功能,可能包括流程图绘制、架构建模、模板管理和定制等。
- 它支持协作设计,可能允许团队成员同时在线编辑和查看设计,以提高工作效率。
- 它可能提供了一个文档管理系统,允许用户轻松管理和访问设计文档,这些文档可能位于/docs目录中。
- 它可能是基于云的服务,能够提供灵活的资源分配,支持按需扩展。
RapidMatter的成功关键在于其能够简化企业架构设计的过程,使得即使是没有专业IT背景的业务人员也能参与到企业架构的设计中来。同时,通过提供一个集中的平台,它有助于统一设计标准和流程,提高设计的一致性和效率。
需要注意的是,RapidMatter的具体实现细节、功能范围、性能指标、安全性、用户界面、用户体验等具体信息并没有在给定的文件信息中披露,因此无法提供更深入的分析和评价。此外,它是否能成功满足不同企业的需求,还需要进一步的市场反馈和用户评价。
总结来说,RapidMatter通过提供基于Web的企业架构设计即服务,旨在简化和优化企业的基础设施设计流程,使得设计更加高效、协作更加顺畅,并可能降低企业在这方面的成本。随着企业对IT基础设施和企业架构设计的需求日益增长,RapidMatter这类服务可能会越来越受欢迎。