首页
如何构建逻辑回归模型并训练模型对数据进行测试以及调整模型参数呢?
如何构建逻辑回归模型并训练模型对数据进行测试以及调整模型参数呢?
时间: 2023-03-13 13:05:41
浏览: 91
要构建逻辑回归模型并训练模型对数据进行测试以及调整模型参数,首先要准备好使用的数据集,然后从中提取有用的特征,再根据这些特征构建模型,使用梯度下降算法(或其他优化算法)进行模型训练,然后使用交叉验证(或其他评估方法)进行模型测试,最后根据测试结果调整模型参数以获得最优结果。
阅读全文
相关推荐
逻辑回归 python代码+训练数据
python实现逻辑回归的例子,值得学习
逻辑回归模型
1.极大似然估计和似然函数 2.LR模型的学习过程 3.其它
如何实现逻辑数据模型
如何实现逻辑数据模型 如何实现逻辑数据模型
模型构建-使用逻辑回归构建模型,lightGBM进行特征筛选 所需数据
接下来,我们可以将数据分为训练集和测试集,然后用训练集训练lightGBM模型进行特征筛选,最后基于筛选后的特征训练逻辑回归模型,并在测试集上评估模型的性能,如准确率、查准率、查全率、F1分数等。 总的来说,这...
爆炸性数据分析-EDA基本和逻辑回归模型:爆炸性数据分析(EDA)基础和逻辑回归模型
在实现逻辑回归模型时,我们首先需要对数据进行预处理,包括缺失值处理、异常值处理、数据标准化或归一化等。接着,我们会将数据分为训练集和测试集,用训练集来训练模型,然后在测试集上评估模型的性能。常用的评估...
机器学习系列7 基于Python的Scikit-learn库构建逻辑回归模型
现在可以创建逻辑回归模型,并使用训练数据拟合模型: python lr = LogisticRegression() lr.fit(X_train, y_train) 模型训练完成后,我们可以使用测试数据进行预测并评估模型性能。这包括计算准确率、混淆...
逻辑回归训练测试的完整代码和数据集
2. **模型构建**:在Python中,我们可以使用sklearn库中的LogisticRegression类来构建逻辑回归模型。首先,我们需要导入必要的库,如numpy、pandas和matplotlib,然后加载数据集,对数据进行预处理,如...
癌症预测数据集,可用逻辑回归完成模型的构建
本数据集包含多个参数,CRIM,ZN,INDUS,CHAS,NX,RM,AGE,DIS,RAD,TAX,PTRATIO,B,LSTAT,MEDV 处理步骤: 1、读取数据 2、选取特征列和目标列 3、数据预处理——缺失值处理和数据归一化 4、预估器流程 5、模型评估与调优
逻辑回归模型实例
在这个实例中,“逻辑回归模型实例”可能是指一个实际应用逻辑回归的案例,涵盖了数据预处理、模型训练、参数调优以及模型评估等多个步骤。这通常涉及到以下关键知识点: 1. **数据预处理**:在建立模型之前,通常...
python实现logistic回归模型和训练数据
**Python实现逻辑回归模型** 逻辑回归(Logistic Regression)是一种广泛应用的分类算法,它通过将线性回归的结果映射到0-1之间,转化为概率预测。在机器学习领域,逻辑回归常用于二分类问题,例如预测一个人是否会...
逻辑回归模型.rar
在训练逻辑回归模型时,我们通常使用最大似然估计法来确定模型参数。目标是最小化似然函数的负对数,即对数似然损失函数(也称为交叉熵损失函数): \[ L(\beta) = -\sum_{i=1}^{n} [y_i\log(p_i) + (1-y_i)\log(1-...
tensorflow实现逻辑回归模型
知识点详解: TensorFlow实现逻辑回归模型的过程中,涉及了以下核心知识点和技术概念。...通过上述步骤,我们可以利用TensorFlow框架构建逻辑回归模型,处理分类问题,并且对模型的性能做出评估。
Face-detection:该任务的目的是用训练算法实现逻辑回归模型,以用于照片中的人脸检测任务。使用模型训练,梯度算法,随机简单梯度算法,正则化,模型选择,操作正确性测试
本项目的目标是利用训练算法实现一个逻辑回归模型,该模型能够对输入的图片进行分析,准确地定位和识别出其中的人脸。在这个过程中,我们将深入探讨以下几个关键知识点: 1. **逻辑回归(Logistic Regression)**:...
Python机器学习金融风控信用评分卡模型源码+数据,信用评分卡模型-逻辑回归模型
3. **模型训练**:使用逻辑回归构建模型,并使用训练数据调整模型参数以优化性能。 4. **模型评估**:使用交叉验证和不同评估指标(如准确率、精确率、召回率、F1分数和AUC-ROC曲线)来衡量模型的性能。 5. **模型...
LogisticRegression逻辑回归模型_逻辑回归_信用预测_
**逻辑回归模型** 逻辑回归(Logistic Regression)是一种广泛应用的分类算法,尤其在二分类问题中表现出色。尽管它的名字中含有“回归”二字,但实际上它主要用于处理离散型输出变量,如是/否、真/假这样的二元...
sklearn逻辑回归测试数据
这个"sklearn逻辑回归测试数据"压缩包提供的是用于训练和评估逻辑回归模型的数据集。下面我们将深入探讨相关知识点。 1. **逻辑回归基础**: 逻辑回归虽然名字中有“回归”二字,但实际上它是一种分类算法。它通过...
线性回归与逻辑回归测试数据
3. 模型训练:使用训练集拟合线性回归或逻辑回归模型,调整模型参数以优化性能。 4. 模型评估:在验证集上进行初步评估,常用的评估指标包括均方误差(MSE)对于线性回归,准确率、查准率、查全率、F1分数和ROC曲线...
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
海量
VIP免费资源
千本
正版电子书
商城
会员专享价
千门
课程&专栏
全年可省5,000元
立即开通
全年可省5,000元
立即开通
大家在看
HN8145XR-V5R021C00S260
HN8145XR_V5R021C00S260固件及V5使能工具等 赚分下文件
基2,8点DIT-FFT,三级流水线verilog实现
基2,8点DIT-FFT,三级流水线verilog实现,输入采用32位输入,计算精度较高,且注释清楚,方便参考。
IBM DS4700磁盘阵列安装配置指南
IBM DS4700磁盘阵列安装配置指南
中南大学943数据结构1997-2020真题&解析
中南大学943数据结构1997-2020真题&解析
DELPHI7+superobject 1.25
DELPHI7 JSON的读取和拼接控件下载。
最新推荐
逻辑回归模型(Logistic)实战应用——文本分类
首先,我们要明确目标:通过逻辑回归模型对文本数据进行分类。数据集包括训练集和测试集,分别用作模型训练和评估。训练集有四个字段,即文章的唯一标识符“id”,正文“article”,词级别“word_seg”,以及预定义...
Python利用逻辑回归模型解决MNIST手写数字识别问题详解
总结起来,Python利用逻辑回归模型解决MNIST手写数字识别问题的过程包括:加载数据、数据预处理、构建模型、选择损失函数、训练模型、验证和测试。在实际应用中,可能会结合更多技术,如正则化、超参数调优、模型...
PyTorch线性回归和逻辑回归实战示例
在PyTorch中实现线性回归和逻辑回归是深度学习初学者经常接触的基本任务,这两个模型也是理解机器学习基础的好入口。线性回归用于预测连续...通过调整模型参数、优化器设置和训练轮数,我们可以进一步优化模型的性能。
博途1200恒压供水程序,恒压供水,一拖三,PID控制,3台循环泵,软启动工作,带超压,缺水保护,西门子1200+KTP1000触摸屏
博途1200恒压供水程序,恒压供水,一拖三,PID控制,3台循环泵,软启动工作,带超压,缺水保护,西门子1200+KTP1000触摸屏
海康无插件摄像头WEB开发包(20200616-20201102163221)
资源摘要信息:"海康无插件开发包" 知识点一:海康品牌简介 海康威视是全球知名的安防监控设备生产与服务提供商,总部位于中国杭州,其产品广泛应用于公共安全、智能交通、智能家居等多个领域。海康的产品以先进的技术、稳定可靠的性能和良好的用户体验著称,在全球监控设备市场占有重要地位。 知识点二:无插件技术 无插件技术指的是在用户访问网页时,无需额外安装或运行浏览器插件即可实现网页内的功能,如播放视频、音频、动画等。这种方式可以提升用户体验,减少安装插件的繁琐过程,同时由于避免了插件可能存在的安全漏洞,也提高了系统的安全性。无插件技术通常依赖HTML5、JavaScript、WebGL等现代网页技术实现。 知识点三:网络视频监控 网络视频监控是指通过IP网络将监控摄像机连接起来,实现实时远程监控的技术。与传统的模拟监控相比,网络视频监控具备传输距离远、布线简单、可远程监控和智能分析等特点。无插件网络视频监控开发包允许开发者在不依赖浏览器插件的情况下,集成视频监控功能到网页中,方便了用户查看和管理。 知识点四:摄像头技术 摄像头是将光学图像转换成电子信号的装置,广泛应用于图像采集、视频通讯、安全监控等领域。现代摄像头技术包括CCD和CMOS传感器技术,以及图像处理、编码压缩等技术。海康作为行业内的领军企业,其摄像头产品线覆盖了从高清到4K甚至更高分辨率的摄像机,同时在图像处理、智能分析等技术上不断创新。 知识点五:WEB开发包的应用 WEB开发包通常包含了实现特定功能所需的脚本、接口文档、API以及示例代码等资源。开发者可以利用这些资源快速地将特定功能集成到自己的网页应用中。对于“海康web无插件开发包.zip”,它可能包含了实现海康摄像头无插件网络视频监控功能的前端代码和API接口等,让开发者能够在不安装任何插件的情况下实现视频流的展示、控制和其他相关功能。 知识点六:技术兼容性与标准化 无插件技术的实现通常需要遵循一定的技术标准和协议,比如支持主流的Web标准和兼容多种浏览器。此外,无插件技术也需要考虑到不同操作系统和浏览器间的兼容性问题,以确保功能的正常使用和用户体验的一致性。 知识点七:安全性能 无插件技术相较于传统插件技术在安全性上具有明显优势。由于减少了外部插件的使用,因此降低了潜在的攻击面和漏洞风险。在涉及监控等安全敏感的领域中,这种技术尤其受到青睐。 知识点八:开发包的更新与维护 从文件名“WEB无插件开发包_20200616_20201102163221”可以推断,该开发包具有版本信息和时间戳,表明它是一个经过时间更新和维护的工具包。在使用此类工具包时,开发者需要关注官方发布的版本更新信息和补丁,及时升级以获得最新的功能和安全修正。 综上所述,海康提供的无插件开发包是针对其摄像头产品的网络视频监控解决方案,这一方案通过现代的无插件网络技术,为开发者提供了方便、安全且标准化的集成方式,以实现便捷的网络视频监控功能。
PCNM空间分析新手必读:R语言实现从入门到精通
 # 摘要 本文旨在介绍PCNM空间分析方法及其在R语言中的实践应用。首先,文章通过介绍PCNM的理论基础和分析步骤,提供了对空间自相关性和PCNM数学原理的深入理解。随后,详细阐述了R语言在空间数据分析中的基础知识和准备工作,以及如何在R语言环境下进行PCNM分析和结果解
生成一个自动打怪的脚本
创建一个自动打怪的游戏脚本通常是针对游戏客户端或特定类型的自动化工具如Roblox Studio、Unity等的定制操作。这类脚本通常是利用游戏内部的逻辑漏洞或API来控制角色的动作,模拟玩家的行为,如移动、攻击怪物。然而,这种行为需要对游戏机制有深入理解,而且很多游戏会有反作弊机制,自动打怪可能会被视为作弊而被封禁。 以下是一个非常基础的Python脚本例子,假设我们是在使用类似PyAutoGUI库模拟键盘输入来控制游戏角色: ```python import pyautogui # 角色位置和怪物位置 player_pos = (0, 0) # 这里是你的角色当前位置 monster
CarMarker-Animation: 地图标记动画及转向库
资源摘要信息:"CarMarker-Animation是一个开源库,旨在帮助开发者在谷歌地图上实现平滑的标记动画效果。通过该库,开发者可以实现标记沿路线移动,并在移动过程中根据道路曲线实现平滑转弯。这不仅提升了用户体验,也增强了地图应用的交互性。 在详细的技术实现上,CarMarker-Animation库可能会涉及到以下几个方面的知识点: 1. 地图API集成:该库可能基于谷歌地图的API进行开发,因此开发者需要有谷歌地图API的使用经验,并了解如何在项目中集成谷歌地图。 2. 动画效果实现:为了实现平滑的动画效果,开发者需要掌握CSS动画或者JavaScript动画的实现方法,包括关键帧动画、过渡动画等。 3. 地图路径计算:标记在地图上的移动需要基于实际的道路网络,因此开发者可能需要使用路径规划算法,如Dijkstra算法或者A*搜索算法,来计算出最合适的路线。 4. 路径平滑处理:仅仅计算出路线是不够的,还需要对路径进行平滑处理,以使标记在转弯时更加自然。这可能涉及到曲线拟合算法,如贝塞尔曲线拟合。 5. 地图交互设计:为了与用户的交互更为友好,开发者需要了解用户界面和用户体验设计原则,并将这些原则应用到动画效果的开发中。 6. 性能优化:在实现复杂的动画效果时,需要考虑程序的性能。开发者需要知道如何优化动画性能,减少卡顿,确保流畅的用户体验。 7. 开源协议遵守:由于CarMarker-Animation是一个开源库,开发者在使用该库时,需要遵守其开源协议,合理使用代码并遵守贡献指南。 此库的文件名'CarMarker-Animation-master'表明这是一个主分支的项目,可能包含源代码文件、示例项目、文档说明等资源。开发者可以通过下载解压缩后获得这些资源,并根据提供的文档来了解如何安装和使用该库。在使用过程中,建议仔细阅读开源项目的贡献指南和使用说明,以确保库的正确集成和使用,同时也可以参与开源社区,与其他开发者共同维护和改进这一项目。"
5G核心网元性能瓶颈揭秘
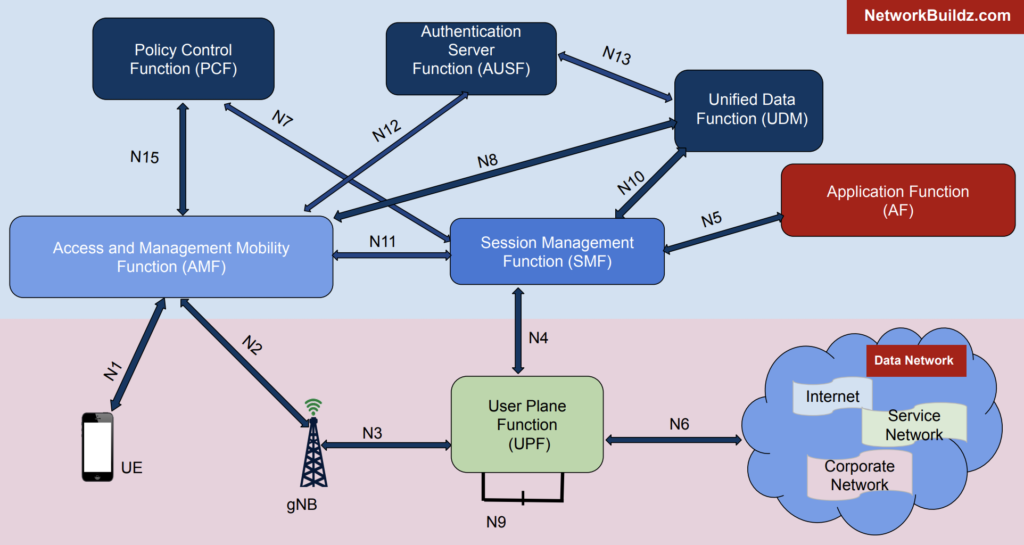 # 摘要 随着5G技术的发展和应用,其核心网的性能优化成为了行业关注的焦点。本文首先概述了5G核心网的架构,并对性能瓶颈进行深入分析,识别了关键的性能指标和瓶颈识别方法。通过案例分析,展示了核心网元常见的性能问题及其诊断和解决过程。随后,文章提出了多项性能优化策略,包括网络设计、系统配置调整以及新技术的应用。此外,本文探讨了安全挑战如何影响核心网的性能,
stm32连接红外传感器并将gsm900a短信收发实现报警
在STM32上连接红外传感器并通过GSM900A模块实现短信报警功能,可以按照以下步骤进行: ### 硬件连接 1. **红外传感器连接**: - 将红外传感器的VCC连接到STM32的3.3V或5V电源(根据传感器规格)。 - 将GND连接到STM32的地线。 - 将GSM900A的VCC连接到外部电源(通常需要2A电流,3.4V-4.4V)。 - 将GND连接到STM32的地线。 - 将TXD引脚连接到STM32的一个UART RX引脚(例如PA10)。 - 将RXD引脚连接到STM32的一个UART TX引脚(例如PA9)。 - 如果需要,可