首页二进制数-0.1101如何转化成IEEE单精度浮点数
二进制数-0.1101如何转化成IEEE单精度浮点数
时间: 2024-07-14 12:00:32 浏览: 120
在计算机科学中,二进制数-0.1101通常用于表示IEEE 754标准定义的单精度浮点数(32位)。该标准将32位分为三个部分:8位符号位、8位指数位和16位尾数(包括隐藏的一位1)。对于-0.1101,我们按照以下步骤转换:
1. **符号位** (1位): 二进制的1表示负数。
2. **指数位** (8位): 首先,我们需要找到对应的偏移量。因为-0.1101不是1.0的整数倍,所以它会以二的负小数幂形式表示。在这种情况下,-0.1101对应的小数范围在-1(1.0的-1次方)和-1/2(1.0的-2次方)之间。指数为-127(正常情况下是-126,但加上隐含的一位1,总指数是-127),因为小数点需要向左移一位。
3. **尾数** (23位): 对于-0.1101,尾数部分是1.0的-2次方,即0.5,二进制为1.0(因为尾数表示的是1减去实际数值)。在表示时,尾数需要补足到23位,通常会在最左边添加足够数量的0。
所以,完整的单精度浮点数表示如下:
- 符号位:0 (正数)
- 指数位:11111111(转换为十进制是-127)
- 尾数(实际值加上隐含的1):0000000000000000001(转换为二进制是0.000000001,即1/2^23)
最终的32位二进制表示是:
0 11111111 0000000000000000001
阅读全文
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
大家在看
基于Python深度学习的目标跟踪系统的设计与实现+全部资料齐全+部署文档.zip
【资源说明】
基于Python深度学习的目标跟踪系统的设计与实现+全部资料齐全+部署文档.zip基于Python深度学习的目标跟踪系统的设计与实现+全部资料齐全+部署文档.zip
【备注】
1、该项目是个人高分项目源码,已获导师指导认可通过,答辩评审分达到95分
2、该资源内项目代码都经过测试运行成功,功能ok的情况下才上传的,请放心下载使用!
3、本项目适合计算机相关专业(人工智能、通信工程、自动化、电子信息、物联网等)的在校学生、老师或者企业员工下载使用,也可作为毕业设计、课程设计、作业、项目初期立项演示等,当然也适合小白学习进阶。
4、如果基础还行,可以在此代码基础上进行修改,以实现其他功能,也可直接用于毕设、课设、作业等。
欢迎下载,沟通交流,互相学习,共同进步!
python版-百家号-seleiunm-全自动发布文案-可多账号-多文案-解放双手 -附带seleiunm源码-二次开发可用
python版_百家号_seleiunm_全自动发布文案_可多账号_多文案_解放双手 _附带seleiunm源码_二次开发可用
NEW.rar_fatherxbi_fpga_verilog 大作业_verilog大作业_投币式手机充电仪
Verilog投币式手机充电仪
清华大学数字电子技术基础课程EDA大作业。刚上电数码管全灭,按开始键后,数码管显示全为0。输入一定数额,数码管显示该数额的两倍对应的时间,按确认后开始倒计时。输入数额最多为20。若10秒没有按键,数码管全灭。
IEC 62133-2-2021最新中文版.rar
IEC 62133-2-2021最新中文版.rar
基于springboot的毕设-疫情网课管理系统(源码+配置说明).zip
基于springboot的毕设-疫情网课管理系统(源码+配置说明).zip
【项目技术】
开发语言:Java
框架:springboot
架构:B/S
数据库:mysql
【实现功能】
网课管理系统分为管理员和学生、教师三个角色的权限子模块。
管理员所能使用的功能主要有:首页、个人中心、学生管理、教师管理、班级管理、课程分类管理、课程表管理、课程信息管理、作业信息管理、请假信息管理、上课签到管理、论坛交流、系统管理等。
学生可以实现首页、个人中心、课程表管理、课程信息管理、作业信息管理、请假信息管理、上课签到管理等。
教师可以实现首页、个人中心、学生管理、班级管理、课程分类管理、课程表管理、课程信息管理、作业信息管理、请假信息管理、上课签到管理、系统管理等。
最新推荐
IEEE标准的32位浮点数转换为十进制的计算方法
这里我们关注的是IEEE标准的32位浮点数如何转换为十进制数,这个问题在单片机编程、数据分析以及MODBUS协议应用中尤为重要。首先,我们要了解IEEE 754浮点数格式,它是计算机科学中用于表示浮点数的标准。 IEEE 754...
对S7-200PLC双精度浮点数转单精度浮点数例程的一点补充
具体实现包括将双精度浮点数的符号位、阶码和尾数部分提取出来,通过一系列二进制运算,包括位的取反、移位和加法运算等,来完成这种转换。这一过程中,二进制与十进制之间的转换以及对IEEE 754标准的深入理解是关键...
C语言菜鸟基础教程之单精度浮点数与双精度浮点数
不管是float还是double,在计算机中的存储都遵循IEEE规范,使用二进制科学计数法,都包含三个部分:符号位、指数位和尾数部分。符号位表示浮点数的符号,即正负号。指数位表示浮点数的指数部分。尾数部分表示浮点数...
Ubuntu 命令技巧手册.rar
Ubuntu命令技巧手册》是专为Ubuntu用户设计的一份实用指南,它涵盖了广泛的操作系统管理、文件处理、网络通信及系统维护等方面的命令行操作技巧。Ubuntu是一个基于Debian的开源Linux发行版,以其用户友好性和强大的命令行工具而受到全球开发者和用户的喜爱。通过熟练掌握这些命令技巧,用户可以更高效地在Ubuntu环境中工作。
手册首先会介绍Ubuntu的基本概念,包括终端的使用和命令行的基本语法。在Linux系统中,终端是执行各种系统级任务的核心工具,用户可以通过键盘输入命令来执行操作,而无需图形化界面。掌握如何打开终端(如通过快捷键Ctrl+Alt+T)以及基本的命令行导航(如cd、ls、pwd)是使用Ubuntu的第一步。
文件和目录管理是Ubuntu命令行中的重要部分。例如,`mkdir`用于创建新目录,`touch`用于创建新文件,`cp`和`mv`分别用于复制和移动文件或目录,而`rm`则用于删除。了解这些命令的选项,如递归操作(-r)和强制删除(-f),能帮助用户更灵活地管理文件系统。
租赁合同编写指南及下载资源
资源摘要信息:《租赁合同》是用于明确出租方与承租方之间的权利和义务关系的法律文件。在实际操作中,一份详尽的租赁合同对于保障交易双方的权益至关重要。租赁合同应当包括但不限于以下要点:
1. 双方基本信息:租赁合同中应明确出租方(房东)和承租方(租客)的名称、地址、联系方式等基本信息。这对于日后可能出现的联系、通知或法律诉讼具有重要意义。
2. 房屋信息:合同中需要详细说明所租赁的房屋的具体信息,包括房屋的位置、面积、结构、用途、设备和家具清单等。这些信息有助于双方对租赁物有清晰的认识。
3. 租赁期限:合同应明确租赁开始和结束的日期,以及租期的长短。租赁期限的约定关系到租金的支付和合同的终止条件。
4. 租金和押金:租金条款应包括租金金额、支付周期、支付方式及押金的数额。同时,应明确规定逾期支付租金的处理方式,以及押金的退还条件和时间。
5. 维修与保养:在租赁期间,房屋的维护和保养责任应明确划分。通常情况下,房东负责房屋的结构和主要设施维修,而租客需负责日常维护及保持房屋的清洁。
6. 使用与限制:合同应规定承租方可以如何使用房屋以及可能的限制。例如,禁止非法用途、允许或禁止宠物、是否可以转租等。
7. 终止与续租:租赁合同应包括租赁关系的解除条件,如提前通知时间、违约责任等。同时,双方可以在合同中约定是否可以续租,以及续租的条件。
8. 解决争议的条款:合同中应明确解决可能出现的争议的途径,包括适用法律、管辖法院等,有助于日后纠纷的快速解决。
9. 其他可能需要的条款:根据具体情况,合同中可能还需要包括关于房屋保险、税费承担、合同变更等内容。
下载资源链接:【下载自www.glzy8.com管理资源吧】Rental contract.DOC
该资源为一份租赁合同模板,对需要进行房屋租赁的个人或机构提供了参考价值。通过对合同条款的详细列举和解释,该文档有助于用户了解和制定自己的租赁合同,从而在房屋租赁交易中更好地保护自己的权益。感兴趣的用户可以通过提供的链接下载文档以获得更深入的了解和实际操作指导。
【项目管理精英必备】:信息系统项目管理师教程习题深度解析(第四版官方教材全面攻略)
# 摘要
信息系统项目管理是确保项目成功交付的关键活动,涉及一系列管理过程和知识领域。本文深入探讨了信息系统项目管理的各个方面,包括项目管理过程组、知识领域、实践案例、管理工具与技术,以及沟通和团队协作。通过分析不同的项目管理方法论(如瀑布、迭代、敏捷和混合模型),并结合具体案例,文章阐述了项目管理的最佳实践和策略。此外,本文还涵盖了项目管理中的沟通管理、团队协作的重要性,
最具代表性的改进过的UNet有哪些?
UNet是一种广泛用于图像分割任务的卷积神经网络结构,它的特点是结合了下采样(编码器部分)和上采样(解码器部分),能够保留细节并生成精确的边界。为了提高性能和适应特定领域的需求,研究者们对原始UNet做了许多改进,以下是几个最具代表性的变种:
1. **DeepLab**系列:由Google开发,通过引入空洞卷积(Atrous Convolution)、全局平均池化(Global Average Pooling)等技术,显著提升了分辨率并保持了特征的多样性。
2. **SegNet**:采用反向传播的方式生成全尺寸的预测图,通过上下采样过程实现了高效的像素级定位。
3. **U-Net+
惠普P1020Plus驱动下载:办公打印新选择
资源摘要信息: "最新惠普P1020Plus官方驱动"
1. 惠普 LaserJet P1020 Plus 激光打印机概述:
惠普 LaserJet P1020 Plus 是惠普公司针对家庭、个人办公以及小型办公室(SOHO)市场推出的一款激光打印机。这款打印机的设计注重小巧体积和便携操作,适合空间有限的工作环境。其紧凑的设计和高效率的打印性能使其成为小型企业或个人用户的理想选择。
2. 技术特点与性能:
- 预热技术:惠普 LaserJet P1020 Plus 使用了0秒预热技术,能够极大减少打印第一张页面所需的等待时间,首页输出时间不到10秒。
- 打印速度:该打印机的打印速度为每分钟14页,适合处理中等规模的打印任务。
- 月打印负荷:月打印负荷高达5000页,保证了在高打印需求下依然能稳定工作。
- 标配硒鼓:标配的2000页打印硒鼓能够为用户提供较长的使用周期,减少了更换耗材的频率,节约了长期使用成本。
3. 系统兼容性:
驱动程序支持的操作系统包括 Windows Vista 64位版本。用户在使用前需要确保自己的操作系统版本与驱动程序兼容,以保证打印机的正常工作。
4. 市场表现:
惠普 LaserJet P1020 Plus 在上市之初便获得了市场的广泛认可,创下了百万销量的辉煌成绩,这在一定程度上证明了其可靠性和用户对其性能的满意。
5. 驱动程序文件信息:
压缩包内包含了适用于该打印机的官方驱动程序文件 "lj1018_1020_1022-HB-pnp-win64-sc.exe"。该文件是安装打印机驱动的执行程序,用户需要下载并运行该程序来安装驱动。
另一个文件 "jb51.net.txt" 从命名上来看可能是一个文本文件,通常这类文件包含了关于驱动程序的安装说明、版本信息或是版权信息等。由于具体内容未提供,无法确定确切的信息。
6. 使用场景:
由于惠普 LaserJet P1020 Plus 的打印速度和负荷能力,它适合那些需要快速、频繁打印文档的用户,例如行政助理、会计或小型法律事务所。它的紧凑设计也使得这款打印机非常适合在桌面上使用,从而不占用过多的办公空间。
7. 后续支持与维护:
用户在购买后可以通过惠普官方网站获取最新的打印机驱动更新以及技术支持。在安装新驱动之前,建议用户先卸载旧的驱动程序,以避免版本冲突或不必要的错误。
8. 其它注意事项:
- 用户在使用打印机时应注意按照官方提供的维护说明定期进行清洁和保养,以确保打印质量和打印机的使用寿命。
- 如果在打印过程中遇到任何问题,应先检查打印机设置、驱动程序是否正确安装以及是否有足够的打印纸张和墨粉。
综上所述,惠普 LaserJet P1020 Plus 是一款性能可靠、易于使用的激光打印机,特别适合小型企业或个人用户。正确的安装和维护可以确保其稳定和高效的打印能力,满足日常办公需求。
数字电路实验技巧:10大策略,让你的实验效率倍增!
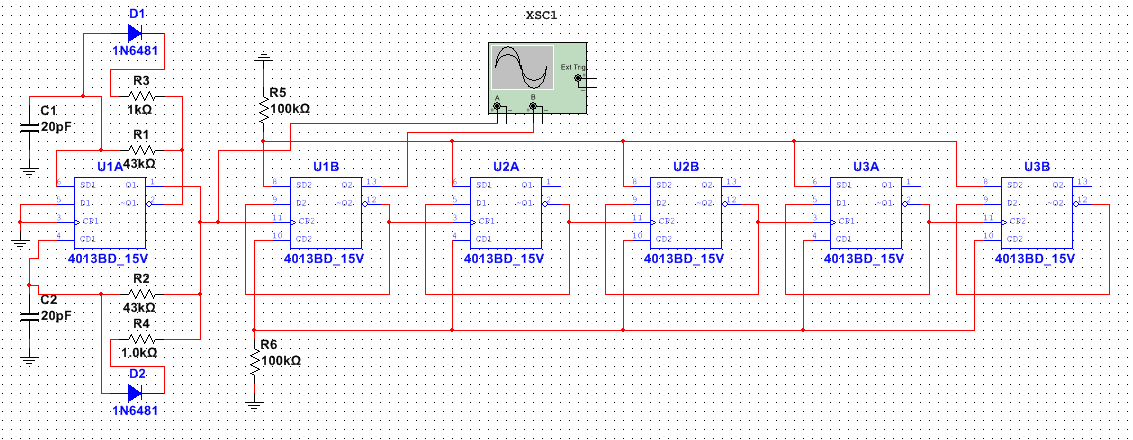
# 摘要
本论文详细介绍了数字电路实验的基础理论、设备使用、设计原则、实践操作、调试与故障排除以及报告撰写与成果展示。首先探讨了数字电路实验所需的基本理论和实验设备的种类与使用技巧,包括测量和故障诊断方法。接着,深入分析了电路设计的原则,涵盖设计流程、逻辑简化、优化策略及实验方案的制定。在实践操作章节中,具体
altium designer布线
### Altium Designer 布线教程和技巧
#### 一、环境设置与准备
为了更高效地完成布线工作,前期的准备工作至关重要。确保原理图已经完全无误并编译成功[^2]。
#### 二、同步查看原理图与PCB布局
通过在原理图标题栏处右键点击并选择 "Split Vertical" 可实现原理图和PCB视图的同时展示,这有助于理解电路连接关系以及提高布线效率。
#### 三、自动布线器配置
Altium Designer内置有强大的自动布线功能。进入“Tools -> PCB Rules and Constraints Editor”,可以自定义诸如最小间距、过孔尺寸等参数来满足