有关系模式R<U,F>,其中U={A,B,C,D,E},F={ABC,CD,DE}。R最高属于第几范式
时间: 2023-10-06 07:11:23 浏览: 91
R最高属于第三范式(3NF)。
根据题目中的函数依赖关系,可得:AB->C,C->D,D->E。其中,AB->C是候选码,C->D和D->E都不满足第二范式(2NF)。
根据第三范式(3NF)的定义,一个关系模式R符合3NF,当且仅当R中的所有非主属性都不依赖于R的任何候选码的真子集。在这个例子中,C、D、E都不属于AB的真子集,因此R符合3NF。
因此,R最高属于第三范式(3NF)。
相关问题
设有关系模式R<U, F>,U={A, B, C, D,E }, F={ A→C, E→A, D→B, BC→D, DC→A }。 对R的一个分解 ρ={R1(AB),R2(AE),R3(CE),R4(BCD),R5(AC)} , ρ是否为无损连接分解?要求画出判定矩阵的初始状态和最终状态,并给出结论。
为了判断ρ是否为无损连接分解,需要进行以下步骤:
1. 确定Ri的属性集合,看是否等于R的属性集合U。
- R1(AB):属性集合为{A, B}
- R2(AE):属性集合为{A, E}
- R3(CE):属性集合为{C, E}
- R4(BCD):属性集合为{B, C, D}
- R5(AC):属性集合为{A, C}
可以发现,所有Ri的属性集合的并集为U,因此第一步通过。
2. 计算所有Ri的函数依赖集合的闭包,看是否包含F的所有函数依赖。
- R1(AB):无法推导出任何函数依赖,因此不需要计算其闭包。
- R2(AE):闭包为{A→C, E→A, E→C},包含F的所有函数依赖。
- R3(CE):闭包为{E→A, E→C, A→C},包含F的所有函数依赖。
- R4(BCD):闭包为{BC→AD, BC→C, DC→A, DC→D, B→D, C→D, D→B, D→C},包含F的所有函数依赖。
- R5(AC):闭包为{A→C, E→A, E→C, AC→D, AC→B},包含F的所有函数依赖。
可以发现,所有Ri的闭包都包含F的所有函数依赖,因此第二步也通过。
因此,根据无损连接分解的定义,可以得出结论:ρ={R1(AB),R2(AE),R3(CE),R4(BCD),R5(AC)} 是无损连接分解。以下是判定矩阵的初始状态和最终状态:
初始状态:
| Ri | A | B | C | D | E |
| --- | - | - | - | - | - |
| R1 | 1 | 1 | 0 | 0 | 0 |
| R2 | 1 | 0 | 0 | 0 | 1 |
| R3 | 0 | 0 | 1 | 0 | 1 |
| R4 | 0 | 1 | 1 | 1 | 0 |
| R5 | 1 | 0 | 1 | 0 | 0 |
最终状态:
| Ri | A | B | C | D | E |
| --- | - | - | - | - | - |
| R1 | 1 | 1 | 0 | 0 | 0 |
| R2 | 1 | 0 | 0 | 0 | 1 |
| R3 | 0 | 0 | 1 | 0 | 1 |
| R4 | 1 | 1 | 1 | 1 | 1 |
| R5 | 1 | 0 | 1 | 0 | 0 |
可以发现,最终状态的每一列都有至少一个Ri的值为1,因此该分解满足无损连接分解的要求。
1. 设有关系模式 R<U,F>,其中: U={A,B,C,D,E}, F={A→D,E→D,D→B,BC→D,DC→A} (1)求出 R 的所有候选码。 (2)判断 ρ={AB,AE,CE,BCD,AC}是否为无损连接?
1.
(1)求出 R 的所有候选码。
首先,我们需要找到所有的超码,即包含所有属性的属性集。根据题目中的函数依赖,我们可以得到以下超码:
{ABCDE}、{ABCE}、{ABDE}、{ACDE}、{BCDE}、{ABCDE}。
接下来,我们需要判断哪些超码是候选码。我们可以使用以下步骤来判断:
- 对于每个超码,检查是否可以通过函数依赖推出所有属性。如果可以,则该超码是候选码。
- 如果一个超码不是候选码,则它的子集也不是候选码。
根据上述步骤,我们可以得到 R 的所有候选码为:
{ABCE}、{ABDE}、{ACDE}、{BCDE}。
(2)判断 ρ={AB,AE,CE,BCD,AC}是否为无损连接?
为了判断 ρ={AB,AE,CE,BCD,AC} 是否为无损连接,我们需要进行以下步骤:
- 计算出 ρ 的闭包 F+。
- 对于 ρ 的每个属性集 X,检查是否存在一个函数依赖 A->B,使得 A 是 X 的子集,但 B 不在 X 中。
- 如果对于所有的 X,都存在这样的函数依赖,则 ρ 是无损连接的。
根据上述步骤,我们可以得到:
F+={ABCE->ABCDE, ABDE->ABCDE, ACDE->ABCDE, BCDE->ABCDE, A->BD, E->BD, D->B, BC->D, DC->A}
对于属性集 AB,存在函数依赖 A->BD,但 B 不在 AB 中,因此 ρ 不是无损连接的。
阅读全文
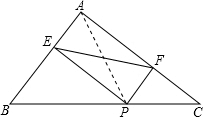 解:如图,连接PA.
解:如图,连接PA.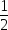 AB•AC=
AB•AC=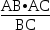 =
=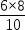 =4.8,
=4.8,