首页5、猴子跳台阶问题 有一只猴子可以向上跳1个台阶,也可以向上跳2个台阶,还可以向上跳3个台阶,有n个台阶,猴子从第1个台阶跳到第n个台阶共有多少种跳法。通过键盘输入台阶数,通过动态规划算法计算出有多少种跳法。C语言
5、猴子跳台阶问题 有一只猴子可以向上跳1个台阶,也可以向上跳2个台阶,还可以向上跳3个台阶,有n个台阶,猴子从第1个台阶跳到第n个台阶共有多少种跳法。通过键盘输入台阶数,通过动态规划算法计算出有多少种跳法。C语言
时间: 2024-04-27 18:09:23 浏览: 66
实现如下:
#include <stdio.h>
int main()
{
int n, i;
printf("请输入台阶数:");
scanf("%d", &n);
int dp[n+1];
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
for(i=3; i<=n; i++)
{
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
}
printf("共有%d种跳法。\n", dp[n]);
return 0;
}
首先,定义一个数组dp,其中dp[i]表示从第1个台阶跳到第i个台阶的跳法数。
由题意可知,当n=1时,猴子只能跳1个台阶,所以dp[1]=1;当n=2时,猴子可以跳1个台阶或者跳2个台阶,所以dp[2]=2;当n=3时,猴子可以跳1个台阶或者跳2个台阶或者跳3个台阶,所以dp[3]=4。
接下来,我们可以通过动态规划的思想,计算出dp数组中其余元素的值。具体地,对于任意的i(4<=i<=n),有dp[i] = dp[i-1] + dp[i-2] + dp[i-3]。即猴子从第i-1个台阶、第i-2个台阶或者第i-3个台阶跳上第i个台阶的跳法数之和。
最后,输出dp[n]即可得到答案。
阅读全文
CSDN会员
开通CSDN年卡参与万元壕礼抽奖
大家在看
2_JFM7VX690T型SRAM型现场可编程门阵列技术手册.pdf
复旦微国产大规模FPGA JFM7VX690T datasheet 手册 资料
网络信息系统应急预案-网上银行业务持续性计划与应急预案
包含4份应急预案
网络信息系统应急预案.doc
信息系统应急预案.DOCX
信息系统(系统瘫痪)应急预案.doc
网上银行业务持续性计划与应急预案.doc
RK eMMC Support List
RK eMMC Support List
DAQ97-90002.pdf
SCPI指令集 详细介绍(安捷伦)
毕业设计&课设-MATLAB的光场工具箱.zip
matlab算法,工具源码,适合毕业设计、课程设计作业,所有源码均经过严格测试,可以直接运行,可以放心下载使用。有任何使用问题欢迎随时与博主沟通,第一时间进行解答!
matlab算法,工具源码,适合毕业设计、课程设计作业,所有源码均经过严格测试,可以直接运行,可以放心下载使用。有任何使用问题欢迎随时与博主沟通,第一时间进行解答!
matlab算法,工具源码,适合毕业设计、课程设计作业,所有源码均经过严格测试,可以直接运行,可以放心下载使用。有任何使用问题欢迎随时与博主沟通,第一时间进行解答!
matlab算法,工具源码,适合毕业设计、课程设计作业,所有源码均经过严格测试,可以直接运行,可以放心下载使用。有任何使用问题欢迎随时与博主沟通,第一时间进行解答!
matlab算法,工具源码,适合毕业设计、课程设计作业,所有源码均经过严格测试,可以直接运行,可以放心下载使用。有任何使用问题欢迎随时与博主沟通,第一时间进行解答!
matlab算法,工具源码,适合毕业设计、课程设计作业,所有源码均经过严格测试,可以直接运行,可以放心下载使用。有任何使用问题欢迎随
最新推荐
【机器人】将ChatGPT飞书机器人钉钉机器人企业微信机器人公众号部署到vercel及docker_pgj.zip
【机器人】将ChatGPT飞书机器人钉钉机器人企业微信机器人公众号部署到vercel及docker_pgj
Python调试器vardbg:动画可视化算法流程
资源摘要信息:"vardbg是一个专为Python设计的简单调试器和事件探查器,它通过生成程序流程的动画可视化效果,增强了算法学习的直观性和互动性。该工具适用于Python 3.6及以上版本,并且由于使用了f-string特性,它要求用户的Python环境必须是3.6或更高。 vardbg是在2019年Google Code-in竞赛期间为CCExtractor项目开发而创建的,它能够跟踪每个变量及其内容的历史记录,并且还能跟踪容器内的元素(如列表、集合和字典等),以便用户能够深入了解程序的状态变化。"
知识点详细说明:
1. Python调试器(Debugger):调试器是开发过程中用于查找和修复代码错误的工具。 vardbg作为一个Python调试器,它为开发者提供了跟踪代码执行、检查变量状态和控制程序流程的能力。通过运行时监控程序,调试器可以发现程序运行时出现的逻辑错误、语法错误和运行时错误等。
2. 事件探查器(Event Profiler):事件探查器是对程序中的特定事件或操作进行记录和分析的工具。 vardbg作为一个事件探查器,可以监控程序中的关键事件,例如变量值的变化和函数调用等,从而帮助开发者理解和优化代码执行路径。
3. 动画可视化效果:vardbg通过生成程序流程的动画可视化图像,使得算法的执行过程变得生动和直观。这对于学习算法的初学者来说尤其有用,因为可视化手段可以提高他们对算法逻辑的理解,并帮助他们更快地掌握复杂的概念。
4. Python版本兼容性:由于vardbg使用了Python的f-string功能,因此它仅兼容Python 3.6及以上版本。f-string是一种格式化字符串的快捷语法,提供了更清晰和简洁的字符串表达方式。开发者在使用vardbg之前,必须确保他们的Python环境满足版本要求。
5. 项目背景和应用:vardbg是在2019年的Google Code-in竞赛中为CCExtractor项目开发的。Google Code-in是一项面向13到17岁的学生开放的竞赛活动,旨在鼓励他们参与开源项目。CCExtractor是一个用于从DVD、Blu-Ray和视频文件中提取字幕信息的软件。vardbg的开发过程中,该项目不仅为学生提供了一个实际开发经验的机会,也展示了学生对开源软件贡献的可能性。
6. 特定功能介绍:
- 跟踪变量历史记录:vardbg能够追踪每个变量在程序执行过程中的历史记录,使得开发者可以查看变量值的任何历史状态,帮助诊断问题所在。
- 容器元素跟踪:vardbg支持跟踪容器类型对象内部元素的变化,包括列表、集合和字典等数据结构。这有助于开发者理解数据结构在算法执行过程中的具体变化情况。
通过上述知识点的详细介绍,可以了解到vardbg作为一个针对Python的调试和探查工具,在提供程序流程动画可视化效果的同时,还通过跟踪变量和容器元素等功能,为Python学习者和开发者提供了强大的支持。它不仅提高了学习算法的效率,也为处理和优化代码提供了强大的辅助功能。
管理建模和仿真的文件
管理Boualem Benatallah引用此版本:布阿利姆·贝纳塔拉。管理建模和仿真。约瑟夫-傅立叶大学-格勒诺布尔第一大学,1996年。法语。NNT:电话:00345357HAL ID:电话:00345357https://theses.hal.science/tel-003453572008年12月9日提交HAL是一个多学科的开放存取档案馆,用于存放和传播科学研究论文,无论它们是否被公开。论文可以来自法国或国外的教学和研究机构,也可以来自公共或私人研究中心。L’archive ouverte pluridisciplinaire
【IT设备维保管理入门指南】:如何制定有效的维护计划,提升设备性能与寿命
# 摘要
本文全面探讨了IT设备维保管理的各个方面,从理论基础到实践案例,再到技术革新和未来展望。首先概述了维保计划的重要性,强调了其在延长设备生命周期和提升性能稳定性方面的作用。接着,文中详细论述了维保计划的制定原则,包括预防性维护、设备分类及成本效益分析等。通过分析不同行业的实践案例,本文揭示了成功维保计划的关键因素,并提出了效果评估与改进的策略。随后,探讨了性能监
python爬取网页链接,url = “https://koubei.16888.com/57233/0-0-0-0”
在Python中,使用如`requests`库来发送HTTP请求并抓取网页链接是比较常见的做法。以下是如何使用`requests`和BeautifulSoup库(用于解析HTML)来爬取给定URL上的信息:
首先,确保已安装`requests`和`beautifulsoup4`库,如果未安装可以使用以下命令安装:
```bash
pip install requests beautifulsoup4
```
然后,你可以编写以下Python脚本来爬取指定URL的内容:
```python
import requests
from bs4 import BeautifulSoup
# 定义要
掌握Web开发:Udacity天气日记项目解析
资源摘要信息: "Udacity-Weather-Journal:Web开发路线的Udacity纳米度-项目2"
知识点:
1. Udacity:Udacity是一个提供在线课程和纳米学位项目的教育平台,涉及IT、数据科学、人工智能、机器学习等众多领域。纳米学位是Udacity提供的一种专业课程认证,通过一系列课程的学习和实践项目,帮助学习者掌握专业技能,并提供就业支持。
2. Web开发路线:Web开发是构建网页和网站的应用程序的过程。学习Web开发通常包括前端开发(涉及HTML、CSS、JavaScript等技术)和后端开发(可能涉及各种服务器端语言和数据库技术)的学习。Web开发路线指的是在学习过程中所遵循的路径和进度安排。
3. 纳米度项目2:在Udacity提供的学习路径中,纳米学位项目通常是实践导向的任务,让学生能够在真实世界的情境中应用所学的知识。这些项目往往需要学生完成一系列具体任务,如开发一个网站、创建一个应用程序等,以此来展示他们所掌握的技能和知识。
4. Udacity-Weather-Journal项目:这个项目听起来是关于创建一个天气日记的Web应用程序。在完成这个项目时,学习者可能需要运用他们关于Web开发的知识,包括前端设计(使用HTML、CSS、Bootstrap等框架设计用户界面),使用JavaScript进行用户交互处理,以及可能的后端开发(如果需要保存用户数据,可能会使用数据库技术如SQLite、MySQL或MongoDB)。
5. 压缩包子文件:这里提到的“压缩包子文件”可能是一个笔误或误解,它可能实际上是指“压缩包文件”(Zip archive)。在文件名称列表中的“Udacity-Weather-journal-master”可能意味着该项目的所有相关文件都被压缩在一个名为“Udacity-Weather-journal-master.zip”的压缩文件中,这通常用于将项目文件归档和传输。
6. 文件名称列表:文件名称列表提供了项目文件的结构概览,它可能包含HTML、CSS、JavaScript文件以及可能的服务器端文件(如Python、Node.js文件等),此外还可能包括项目依赖文件(如package.json、requirements.txt等),以及项目文档和说明。
7. 实际项目开发流程:在开发像Udacity-Weather-Journal这样的项目时,学习者可能需要经历需求分析、设计、编码、测试和部署等阶段。在每个阶段,他们需要应用他们所学的理论知识,并解决在项目开发过程中遇到的实际问题。
8. 技术栈:虽然具体的技术栈未在标题和描述中明确提及,但一个典型的Web开发项目可能涉及的技术包括但不限于HTML5、CSS3、JavaScript(可能使用框架如React.js、Angular.js或Vue.js)、Bootstrap、Node.js、Express.js、数据库技术(如上所述),以及版本控制系统如Git。
9. 学习成果展示:完成这样的项目后,学习者将拥有一个可部署的Web应用程序,以及一个展示他们技术能力的项目案例,这些对于未来的求职和职业发展都是有价值的。
10. 知识点整合:在进行Udacity-Weather-Journal项目时,学习者需要将所学的多个知识点融合在一起,包括前端设计、用户体验、后端逻辑处理、数据存储和检索、以及可能的API调用等。
总结来说,Udacity-Weather-Journal项目是Udacity Web开发纳米学位课程中的一个重要实践环节,它要求学习者运用他们所学到的前端和后端开发技能,完成一个具体的Web应用程序项目。通过完成这样的项目,学习者能够将理论知识转化为实践经验,并为他们未来在IT行业的职业发展打下坚实的基础。
"互动学习:行动中的多样性与论文攻读经历"
多样性她- 事实上SCI NCES你的时间表ECOLEDO C Tora SC和NCESPOUR l’Ingén学习互动,互动学习以行动为中心的强化学习学会互动,互动学习,以行动为中心的强化学习计算机科学博士论文于2021年9月28日在Villeneuve d'Asq公开支持马修·瑟林评审团主席法布里斯·勒菲弗尔阿维尼翁大学教授论文指导奥利维尔·皮耶昆谷歌研究教授:智囊团论文联合主任菲利普·普雷教授,大学。里尔/CRISTAL/因里亚报告员奥利维耶·西格德索邦大学报告员卢多维奇·德诺耶教授,Facebook /索邦大学审查员越南圣迈IMT Atlantic高级讲师邀请弗洛里安·斯特鲁布博士,Deepmind对于那些及时看到自己错误的人...3谢谢你首先,我要感谢我的两位博士生导师Olivier和Philippe。奥利维尔,"站在巨人的肩膀上"这句话对你来说完全有意义了。从科学上讲,你知道在这篇论文的(许多)错误中,你是我可以依
【文献整理高效法】:ENDNOTE软件实用功能及快捷操作揭秘
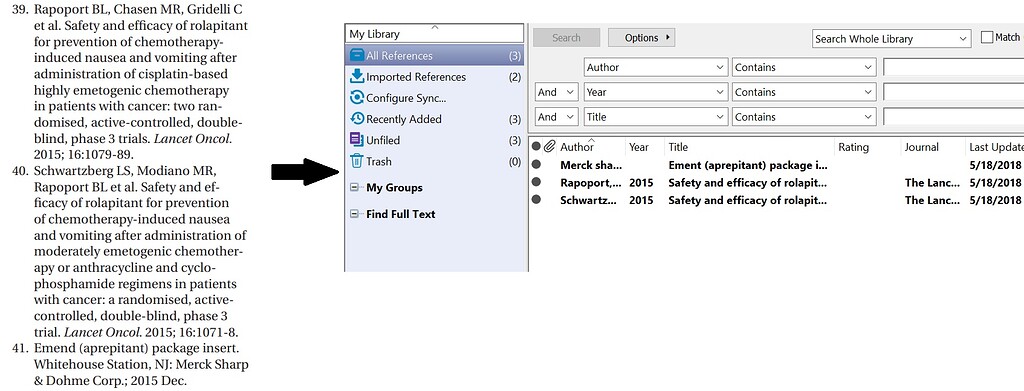
# 摘要
本文综合探讨了ENDNOTE在文献整理和管理中的作用及其高效操作技巧。首先介绍了文献整理的重要性和ENDNOTE软件的简介,随后深入解析了ENDNOTE的基本功能,包括文献信息的导入与管理、引用和参考文献的生成,以及文献搜索与数据库集成。接着,本文详细阐述了ENDNOTE的高效操作技巧,涵
在使用SQL创建存储过程时,是否可以在定义输入参数时直接为其赋予初始值?
在使用SQL创建存储过程时,通常可以在定义输入参数时为其赋予初始值。这种做法可以使参数具有默认值,当调用存储过程时,如果没有提供该参数的值,则会使用默认值。以下是一个示例:
```sql
CREATE PROCEDURE MyProcedure
@Param1 INT = 10,
@Param2 NVARCHAR(50) = 'DefaultValue'
AS
BEGIN
-- 存储过程的主体
SELECT @Param1 AS Param1, @Param2 AS Param2
END
```
在这个示例中,`@Param1`和`@Param2`是输入参数
MySQL 5.5.28 64位数据库软件免费下载
资源摘要信息:"mysql 64位.zip"
知识点:
1. MySQL简介:
MySQL是一个流行的关系型数据库管理系统(RDBMS),由瑞典MySQL AB公司开发,目前被Oracle公司所拥有。它使用结构化查询语言(SQL)进行数据库管理,是基于客户端-服务器模型的数据库系统,能够处理拥有上千万条记录的大型数据库。
2. MySQL版本:
标题中提到的“mysql 5.5.28版本”指的是MySQL数据库管理系统的一个具体版本。每个版本号由主版本号、次版本号和修订号组成,通常表示该版本在功能、性能以及稳定性等方面相对于前一个版本的改进。在这个案例中,5.5代表主版本号,28代表修订号。
3. 64位版本:
"64位"指的是软件运行所需的操作系统和处理器支持的位数。64位系统比32位系统能够处理更大的内存和更复杂的应用程序。因此,如果一个软件提供64位版本,则意味着它可以充分利用64位系统的优势,提高程序运行的效率和稳定性。
4. Windows系统:
"Windows系统"指的是微软公司开发的一系列操作系统,其中包括家庭用户广泛使用的Windows XP、Windows 7、Windows 8和Windows 10等。MySQL 5.5.28 64位版本专门为Windows操作系统设计,确保了用户在使用Windows系统时的兼容性和运行效率。
5. 免费开源:
MySQL是一个开源软件,遵循GPL(GNU通用公共许可证),这意味着任何人都可以免费下载、使用、修改和重新分发MySQL。开源特性使得MySQL社区活跃,不断有开发者为其贡献代码,增强了MySQL的功能和稳定性。
6. 数据库存储:
MySQL的最主要功能是数据存储和管理。作为关系型数据库,它将数据存储在表格中,表格之间通过主键和外键进行关联。MySQL支持多种数据类型,例如整型、浮点型、字符型、日期时间型等。通过SQL语句,用户可以创建、查询、更新和删除数据库中的记录。
7. 下载使用:
资源标题中提到“欢迎下载使用”,意味着用户可以免费获取这个MySQL版本。用户可以通过官方网站或其他提供该软件的站点进行下载。下载安装后,用户需要配置数据库环境,然后才能进行数据库设计、开发和管理等工作。
综上所述,该资源为64位版本的MySQL 5.5.28,专为Windows系统设计,用户可以免费下载使用。它是一个功能强大的数据库管理系统,适用于数据存储和管理,尤其适合处理大量数据的场合。用户下载安装该资源后,可以开始使用MySQL提供的丰富功能,包括创建数据库、设计表结构、进行数据查询和维护等操作。