MATLAB模型预测控制多目标优化：解决方法全解析

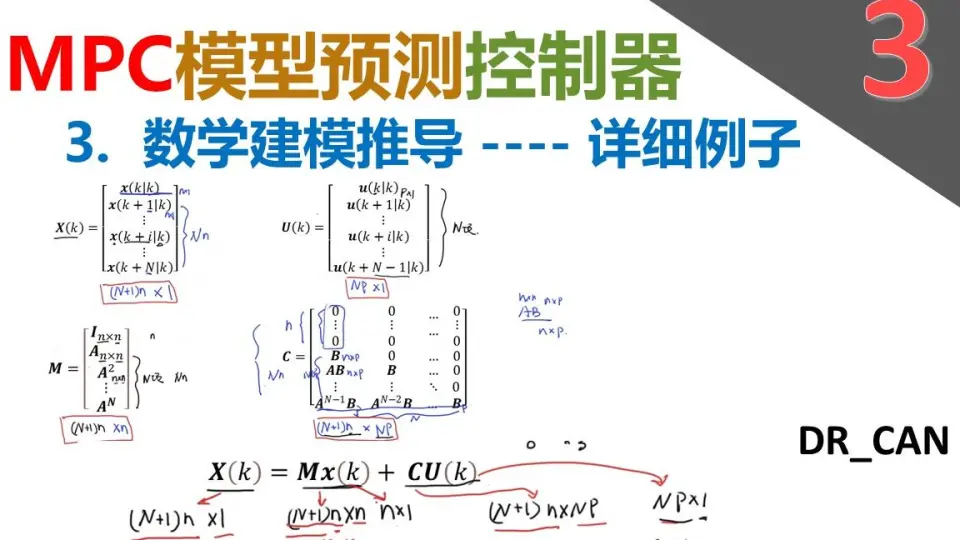
# 1. 模型预测控制基础

## 1.1 模型预测控制（MPC）的起源
模型预测控制是一种先进的控制策略，起源于20世纪70年代，用于解决工业过程控制中的复杂问题。它通过优化一个有限时间范围内的控制策略来预测未来的系统行为，并实时调整输入变量以确保系统的最佳性能。

## 1.2 MPC的工作原理
MPC的核心思想是使用一个数学模型来预测未来一段时间内系统的输出响应。它以当前的系统状态作为起点，通过求解一个在线优化问题来计算最优控制序列。这些控制序列仅仅应用当前的控制动作，之后整个优化过程在下一个采样时刻重复。

## 1.3 MPC的应用领域
由于MPC能够处理多变量、多约束的复杂系统，它广泛应用于化工、石油、电力以及汽车等工业领域。MPC可以根据实际应用需求进行定制，适应各种操作条件和性能指标，从而在众多领域显示出了巨大的应用潜力。

# 2. 多目标优化理论与方法

## 2.1 多目标优化问题概述

### 2.1.1 定义和特点

多目标优化问题（Multi-Objective Optimization Problem, MOOP）是在决策变量的选择上存在多个冲突目标的优化问题。在这种情况下，我们寻求一个解的集合，这些解被称为Pareto最优解，它意味着无法通过改进某个目标而不损害其他目标来改进任何一个解。这样的解集合反映了不同目标之间的权衡关系，为决策者提供了一系列的最优选择。

多目标优化的特点包括：
- **多目标性**：存在至少两个需要同时优化的目标函数。
- **冲突性**：各个目标之间可能存在冲突，优化其中一个目标可能会导致其他目标性能下降。
- **非劣解**：优化过程中产生的非劣解，也就是Pareto最优解，是没有任何一个目标可以同时被改善而不使其他目标变得更差的解。
- **选择困难**：需要在多个非劣解之间做出最终决策，这通常取决于决策者的偏好。

### 2.1.2 多目标优化的分类

多目标优化问题可以根据多个维度进行分类，常见的分类方法包括：
- **按目标的数量分类**：可以分为双目标优化、三目标优化以及多目标优化。
- **按决策变量的数量分类**：可以分为低维多目标优化和高维多目标优化。
- **按问题的性质分类**：可以分为连续多目标优化和离散多目标优化。
- **按目标函数间的关系分类**：可以分为协调优化问题（目标间关系和谐）和非协调优化问题（目标间存在严重的冲突）。

## 2.2 多目标优化算法

### 2.2.1 Pareto优化基础

Pareto优化理论是多目标优化的基础，它由意大利经济学家 Vilfredo Pareto 在20世纪初提出。在多目标优化中，Pareto优势的概念是核心。一个解x优于另一个解y，当且仅当x在所有目标上都不逊于y，并且至少在一个目标上优于y。所有非被其他解Pareto优势的解称为Pareto最优解。Pareto最优解的集合称为Pareto前沿。

### 2.2.2 典型多目标优化算法

多目标优化算法的种类繁多，其中一些算法由于其有效性、效率和普遍适用性，成为研究和应用的热点：
- **NSGA-II (Non-dominated Sorting Genetic Algorithm II)**：一种基于遗传算法的多目标优化方法，它采用非支配排序和拥挤距离来保持种群的多样性。
- **SPEA2 (Strength Pareto Evolutionary Algorithm 2)**：通过改进的适应度分配策略和Pareto排序来提高解的质量和多样性。
- **MOEA/D (Multi-Objective Evolutionary Algorithm based on Decomposition)**：一种基于分解的方法，将多目标问题分解为多个单目标子问题，并协同求解。

## 2.3 MATLAB中多目标优化工具箱

### 2.3.1 工具箱简介

MATLAB提供了多目标优化工具箱（Multi-Objective Optimization Toolbox），这是一个用于多目标问题求解的集成环境。该工具箱提供了一系列算法、函数和方法，使用户能够定义问题、选择算法、执行优化、分析结果，并可视化Pareto前沿。工具箱支持连续和离散变量的优化问题，以及线性和非线性目标函数和约束。

### 2.3.2 工具箱中的算法与函数

MATLAB多目标优化工具箱包括了多种用于多目标问题求解的算法，如`gamultiobj`、`paretosearch`等，以及一系列辅助函数，这些函数支持：
- 定义多目标问题：`optimoptions`用于设置优化选项。
- 执行优化：`gamultiobj`利用遗传算法实现多目标优化。
- 结果分析与可视化：`paretoregion`和`plotpareto`用于分析和可视化Pareto前沿。

### 2.3.2.1 使用gamultiobj函数的示例

% 定义多目标函数，这里使用两个标准测试函数Sphere和Rastrigin
fun = @(x) [sum(x.^2), sum((x-2).^2)];

% 设置优化选项
options = optimoptions('gamultiobj','PlotFcn',@gaplotpareto);

% 执行优化
[x,fval] = gamultiobj(fun, 2, [], [], [], [], [], [], [], options);

% 输出结果
disp('Pareto 前端的点');
disp(x);
disp('Pareto 前端点的目标函数值');
disp(fval);

在上述代码中，`gamultiobj`函数用于求解多目标优化问题，其中`fun`定义了两个目标函数。`options`指定了优化算法的选项，这里特别指定了绘图函数`gaplotpareto`来可视化Pareto前沿。最终，函数返回了Pareto前沿的点以及它们的目标函数值。

# 3. MATLAB模型预测控制实现

模型预测控制（Model Predictive Control，MPC）是一种先进的控制策略，在工业领域有广泛应用。它通过在每一个控制步骤内解决一个在线优化问题，以预测未来的行为，并将其与期望的性能目标进行比较，从而得到最佳控制动作。在MATLAB环境中，Model Predictive Control