【自定义层集成】：PyTorch迁移学习中添加新层的秘密

# 1. PyTorch迁移学习概述

## 1.1 迁移学习的重要性

在现代深度学习领域，迁移学习已经成为一种至关重要的技术，它允许我们将一个领域训练好的模型应用到另一个领域。这不仅能够缩短训练时间，还能在数据量较小的新领域上实现较好的性能。PyTorch作为当下流行的深度学习框架之一，其提供的迁移学习工具与API使得复杂的迁移学习任务变得更加简便。

## 1.2 PyTorch迁移学习的优势

PyTorch的动态计算图特性使得模型的修改和调试更加灵活。此外，它丰富的社区资源和易用的API使得PyTorch成为研究和工业界进行迁移学习的首选。利用预训练模型进行微调(fine-tuning)，或是提取特征进行预测，都是迁移学习在PyTorch中的常用方式。

## 1.3 应用场景与效果预期

迁移学习在图像识别、自然语言处理等众多领域已有广泛应用。在有限的计算资源和时间成本下，通过迁移学习能够迅速部署有效的深度学习模型。本章节将介绍迁移学习的基本概念，并为读者后续章节的深入学习打下坚实的基础。

# 2. PyTorch基础和自定义层集成理论

## 2.1 PyTorch基础知识回顾
### 2.1.1 张量操作和自动微分

PyTorch的核心是张量操作和自动微分，这是构建和训练深度学习模型的基础。一个张量可以被看作一个多维数组，用于存储数据。在PyTorch中，张量的操作遵循和NumPy类似的理念，提供了广泛的函数来进行数学运算、索引、切片、切块等操作。

使用PyTorch中的张量操作和自动微分系统可以容易地实现复杂的数学运算，并且自动计算梯度，极大地简化了深度学习模型的训练过程。这一特性基于计算图的概念，计算图记录了数据和操作的流程，通过反向传播算法，可以快速地计算梯度，用于网络参数的更新。

下面是一个简单的例子，展示如何创建张量并进行基本操作：

import torch

# 创建一个张量
a = torch.tensor([1., 2., 3.])

# 对张量进行一些操作
b = a + 2
c = torch.mean(b)

print("a:", a)
print("b:", b)
print("c:", c)

该代码块创建了一个包含三个元素的一维张量，并对张量中的每个元素加2，最后计算了加2之后的平均值。这些都是基本的张量操作，而PyTorch的威力在于能够自动追踪这些操作，并计算出梯度。

### 2.1.2 模型定义和参数优化

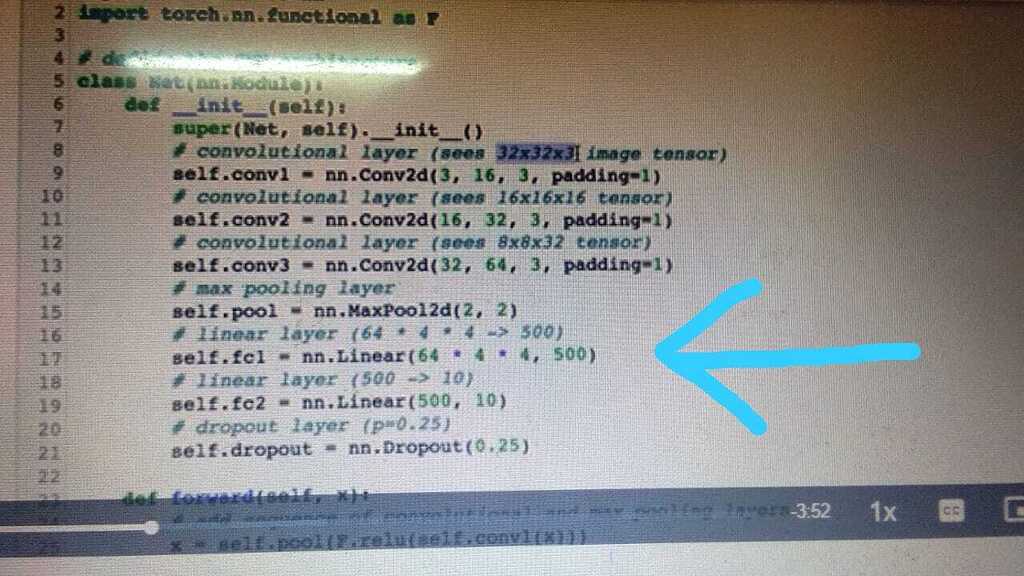
定义深度学习模型是PyTorch的另一项基础任务。在PyTorch中，模型通常通过继承`nn.Module`类并定义`__init__`方法和`forward`方法来构建。`__init__`方法用于初始化模型的层，而`forward`方法定义了数据通过这些层的路径。

参数优化则是通过定义损失函数和选择优化器来完成的。损失函数衡量的是模型输出和真实值之间的差异，而优化器则负责根据这个差异更新模型的参数。

这里是一个简单的线性回归模型的定义和训练过程：

import torch
import torch.nn as nn
import torch.optim as optim

# 定义一个简单的线性模型
class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # 输入和输出维度都是1

    def forward(self, x):
        return self.linear(x)

# 实例化模型
model = LinearRegressionModel()

# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 假设我们有一组简单的输入和输出数据
inputs = torch.randn(10, 1)
targets = torch.randn(10, 1)

# 训练模型
num_epochs = 100
for epoch in range(num_epochs):
    optimizer.zero_grad()   # 清空上一步的梯度
    outputs = model(inputs)  # 前向传播
    loss = criterion(outputs, targets)  # 计算损失
    loss.backward()   # 反向传播计算梯度
    optimizer.step()  # 更新参数
    if (epoch+1) % 10 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

在这个例子中，我们首先定义了一个线性回归模型类，它继承自`nn.Module`，并在`forward`方法中指定了数据的流动方式。然后，我们使用均方误差损失函数和随机梯度下降优化器来训练模型。在每一步的训练中，我们清空梯度，计算损失，反向传播梯度，最后更新模型参数。通过这种方式，模型参数逐渐优化，直到损失最小化。

## 2.2 自定义层集成的理论基础

### 2.2.1 神经网络层的设计原则

设计神经网络层（也称为层或模块）需要遵循一些原则以确保其有效性和效率。首先，层应该能够执行一个或多个具体的转换函数，如卷积、池化、归一化等。其次，层需要能够适应不同大小和维度的输入。此外，层的设计应该考虑性能和内存占用，以确保在大规模数据集上的可扩展性和实用性。

在设计自定义层时，还需要考虑如何高效地计算梯度，以及如何有效地利用GPU加速，因为这些因素直接影响到模型的训练速度和效果。

### 2.2.2 自定义层的必要性和优势

自定义层的必要性来自于深度学习的多样性和特定应用场景的需求。标准化层可能无法满足所有需求，特别是在一些特定领域如医学图像分析、自然语言处理、强化学习等。此外，自定义层可以提供更高的灵活性，允许研究人员和工程师构建和实验新的架构和方法。

自定义层的优势包括：

- **更高的灵活性**：允许研究人员自由设计网络结构。
- **更好的性能**：针对特定问题优化的层可以提高性能。
- **模型的可解释性**：可以通过自定义层来提高模型的透明度和解释能力。
- **创新的驱动力**：自定义层鼓励创新和尝试新的网络结构。

### 2.2.3 面临的挑战和解决方案

自定义层面临的主要挑战之一是设计复杂性。创建一个性能良好且能够稳定工作的层需要深入理解相关的数学和算法。此外，调试和测试自定义层也是困难的部分，因为错误可能会在任何地方出现，且难以追踪。

解决方案包括：

- **模块化设计**：确保自定义层可重用和可组合。
- **严格测试**：编写详尽的单元测试来确保层的正确性。
- **使用抽象**：利用PyTorch提供的高层抽象来简化设计。
- **社区贡献**：与其他研究人员合作并从社区获得反馈。

通过这些策略，可以克服自定义层设计和集成过程中遇到的挑战。

## 2.3 迁移学习的基本流程

### 2.3.1 迁移学习的基本流程

迁移学习是利用在一个任务上学到的知识来帮助解决另一个相关但不同的任务。在深度学习中，这通常意味着使用在大规模数据集上预训练的模型作为新模型的起点。

迁移学习的基本流程可以概括为以下步骤：

1. **选择源模型**：选择一个在类似任务上预训练好的模型，如在ImageNet上预训练的模型。
2. **特征提取**：将预训练模型作为一个固定的特征提取器使用，只调整最后一层或最后几层以适应新任务。
3. **微调**：在新数据集上继续训练模型的全部或部分层。在此过程中，学习率通常较低，以避免破坏预训练的权重。
4. **评估**：在验证集上评估模型的性能，确保迁移学习提升了模型在新任务上的表现。

下面是一个使用迁移学习对图像进行分类的示例代码：

import torch
import torchvision.models as models
import torchvision.transforms as transforms
from torchvision.datasets import ImageFolder
from torch.utils.data import DataLoader

# 下载预训练模型
model = models.resnet18(pretrained=True)

# 替换最后一层以适应新的分类任务
model.fc = nn.Linear(model.fc.in_features, num_classes)

# 定义数据预处理
transform = transforms.Compose([
    transforms.Resize(256),
    transforms.CenterCrop(224),
    transforms.ToTensor(),
    transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]),
])

# 加载数据集
data = ImageFolder(root='path_to_new_dataset', transform=transform)
trainloader = DataLoader(data, batch_size=32, shuffle=True)

# 微调模型
for param in model.parameters():
    param.requires_grad = True

criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 训练模型
num_epochs = 10
for epoch in range(num_epochs):
    running_loss = 0.0
    for inputs, labels in trainloader:
        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()
    print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {run