【递推关系与生成函数】：掌握解决复杂问题的数学工具


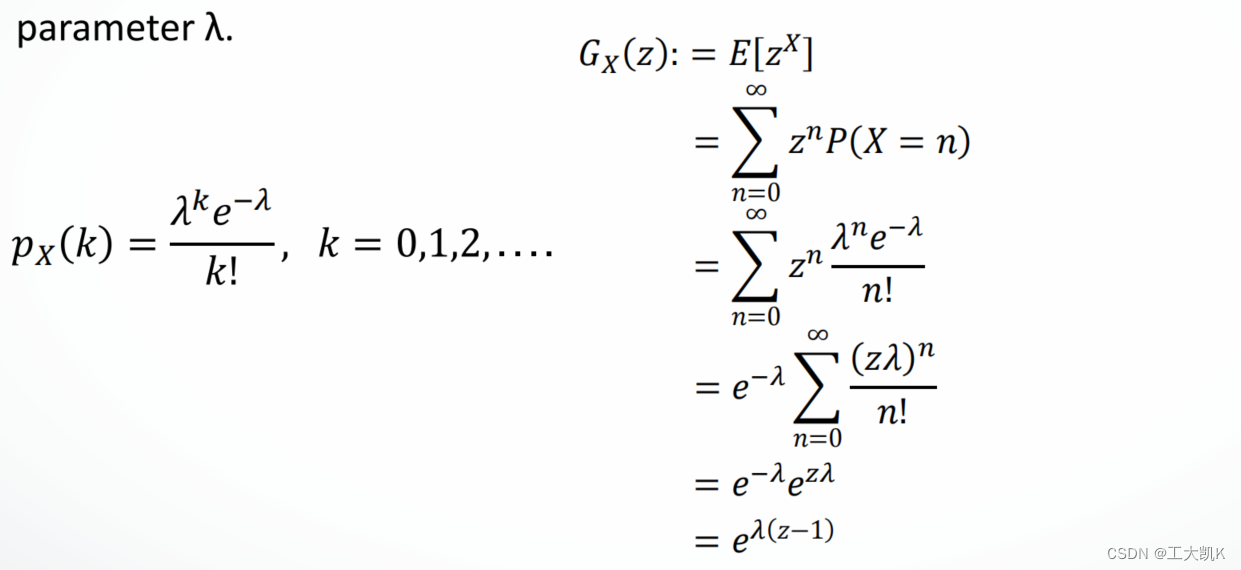
参考资源链接：[广工离散数学anyview答案(16届最新完整版)](https://wenku.csdn.net/doc/6412b5e1be7fbd1778d44bab?spm=1055.2635.3001.10343)
# 1. 递推关系与生成函数概述

在数学与计算机科学中，递推关系和生成函数是两种重要的理论工具，它们在解决各类离散问题中扮演着核心角色。递推关系是描述序列间相互依赖的数学表达式，而生成函数则提供了一种以代数形式解决组合问题的方法。

## 1.1 递推关系基础

递推关系通过给定序列的前几项来定义后续项，这使得复杂序列的分析与生成变得可行。递推关系的特性使其成为研究序列增长模式和结构的重要手段。

## 1.2 生成函数的作用

生成函数则将数列中的项与变量的幂次关联起来，通过研究生成函数的性质，可以推导出序列的封闭形式、求和问题及极限性质等。例如，通过生成函数，可以将复杂问题转化为简单的代数操作，从而得出解决问题的途径。

## 1.3 递推关系与生成函数的结合

当递推关系与生成函数结合时，可以展示出它们在离散数学中的强大威力。利用生成函数解析递推关系，不仅可以解决组合问题，还可以应用于概率论、物理、工程学以及计算机科学的多个领域。

递推关系与生成函数为研究离散问题提供了一种强有力的视角，下一章我们将深入探讨递推关系的基本理论和应用。

# 2. 递推关系的基本理论与应用

## 2.1 递推关系的定义和分类
### 2.1.1 线性递推关系
线性递推关系是递推关系中最简单也是最常见的一种类型，其一般形式为：

\[ a_n = c_1a_{n-1} + c_2a_{n-2} + \cdots + c_ka_{n-k} + f(n) \]

其中，\(a_n\) 表示数列的第 \(n\) 项，\(c_1, c_2, \ldots, c_k\) 是常数，\(f(n)\) 是一个与 \(n\) 有关的函数，通常为 \(0\)。当 \(f(n)\) 为 \(0\) 时，该线性递推关系被称为齐次的；否则，称为非齐次的。

表 2.1.1.1 展示了线性递推关系的不同分类及其特点：

| 分类 | 描述 | 示例 |
| --- | --- | --- |
| 齐次线性递推关系 | \(f(n) = 0\) | \(a_n = a_{n-1} + a_{n-2}\) |
| 非齐次线性递推关系 | \(f(n) \neq 0\) | \(a_n = a_{n-1} + n\) |

线性递推关系的解法通常依赖于特征方程法，通过解特征方程来找到通项公式。

### 2.1.2 非线性递推关系
非线性递推关系是更为复杂的递推形式，其一般形式不满足线性特性，通常包含项的乘积、幂等运算。例如：

\[ a_n = a_{n-1} \cdot a_{n-2} \]

表 2.1.2.1 展示了非线性递推关系的分类及其特点：

| 分类 | 描述 | 示例 |
| --- | --- | --- |
| 乘法递推关系 | \(a_n\) 是前几项的乘积形式 | \(a_n = a_{n-1} \cdot a_{n-2}\) |
| 幂递推关系 | \(a_n\) 是前几项的幂形式 | \(a_n = (a_{n-1})^{a_{n-2}}\) |

非线性递推关系的解法比线性递推关系更加多样，常用的方法包括迭代法、不动点法和特殊数学工具（如高等数学中的特殊函数）。

## 2.2 递推关系的解法和性质
### 2.2.1 初等方法解递推关系
对于一些简单的线性递推关系，如一阶和二阶递推关系，可以使用初等数学方法来求解。这里以一阶线性齐次递推关系为例：

\[ a_n = c \cdot a_{n-1} \]

表 2.2.1.1 展示了解一阶线性齐次递推关系的步骤：

1. 写出递推关系式。
2. 对递推关系两边取对数得到 \( \log a_n = \log c + \log a_{n-1} \)。
3. 利用 \( \log a_{n-1} \) 可以表示为 \( \log a_1 + (n-1)\log c \)。
4. 将结果代回得到 \( \log a_n = \log a_1 + n \log c \)。
5. 两边同时取指数，得到 \( a_n = a_1 \cdot c^n \)。

### 2.2.2 特征方程法
对于线性齐次递推关系，特征方程法是一个非常有效的解法。以二阶线性齐次递推关系为例：

\[ a_n = c_1a_{n-1} + c_2a_{n-2} \]

表 2.2.2.1 展示了解二阶线性齐次递推关系的步骤：

1. 写出递推关系的特征方程 \( r^2 = c_1r + c_2 \)。
2. 求出特征方程的根 \( r_1 \) 和 \( r_2 \)。
3. 分别考虑三种情况：两个不同的实数根、一个重根、复数根。
4. 根据不同的情况写出递推关系的通项公式。
5. 使用初始条件求出通项公式中的特定常数。

### 2.2.3 复杂递推关系的处理技巧
复杂递推关系通常不具有显而易见的解析解。处理这类问题时，我们通常采用以下方法：

1. **特征根理论**：对于非齐次线性递推关系，首先找到对应的齐次递推关系的特征根，然后通过待定系数法求解非齐次递推关系。

2. **变换方法**：通过某种数学变换（如Z变换、L变换等）将递推关系转换为更易处理的形式。

3. **近似方法**：对于不能精确求解的递推关系，可以使用近似方法，例如数值逼近法或渐近分析方法。

4. **计算机辅助**：使用计算机程序进行迭代计算，获得递推关系的数值解。

## 2.3 递推关系在计数问题中的应用
### 2.3.1 组合计数问题的递推解法
递推关系在组合计数问题中有着广泛的应用。以下是一个使用递推关系解决组合计数问题的例子：

**问题描述**：在一个 \(n \times n\) 的棋盘上，从左上角到右下角，每次只能向下或向右移动一格，有多少种不同的路径？

**递推解法**：

1. 设 \(a_{i,j}\) 为从左上角到棋盘上 \( (i, j) \) 位置的不同路径数。
2. 那么 \(a_{i+1,j}\) 和 \(a_{i,j+1}\) 为从当前位置出发到右下角的路径数，因此有递推关系式：
\[ a_{i+1,j} = a_{i,j} + a_{i,j+1} \]
3