堆的应用之九：求解滑动窗口中的中值

# 1. 堆的基本概念和操作**

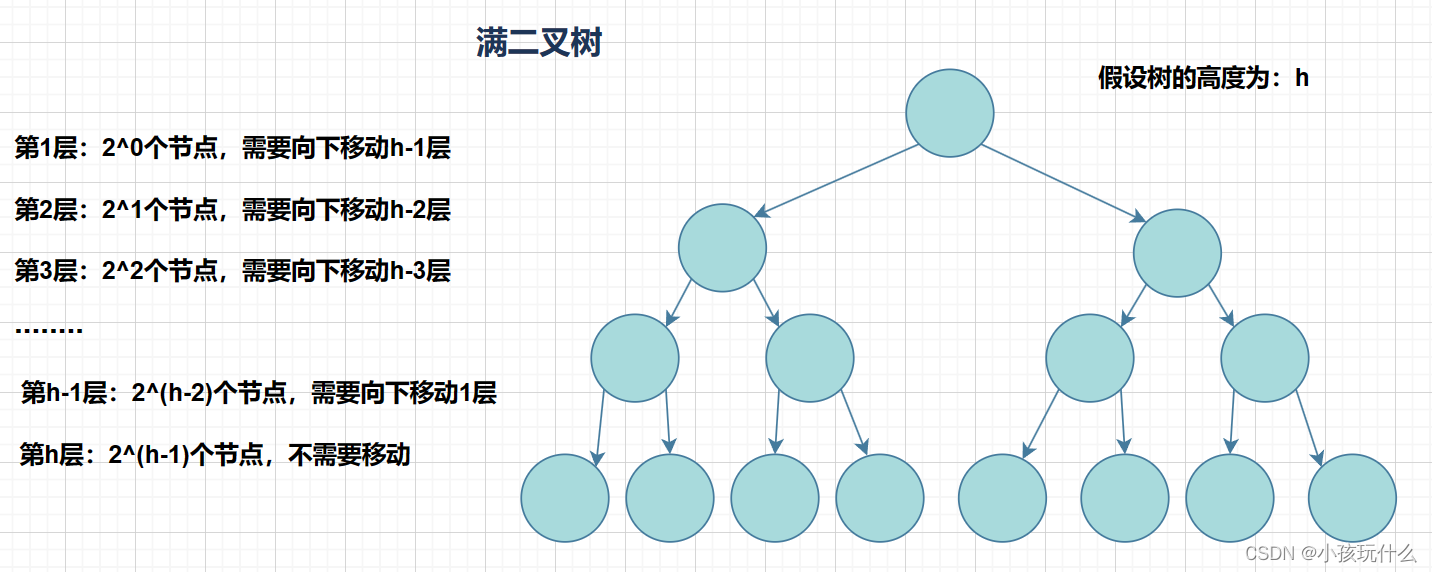
堆是一种基于完全二叉树的数据结构，具有以下特性：

* 每个节点的值都大于或等于其子节点的值（小顶堆）或小于或等于其子节点的值（大根堆）。
* 除了最底层之外，所有层都完全填充。

# 2. 堆的应用：求解滑动窗口中的中值

### 2.1 问题背景和算法概述

在数据分析和机器学习等领域中，经常需要处理滑动窗口中的数据。滑动窗口是一种在数据流中移动的固定大小的窗口，它允许我们专注于数据流中特定时间范围内的子集。

求解滑动窗口中的中值是一个常见的问题，它要求我们计算窗口中所有元素的中值，随着窗口在数据流中移动，中值也会动态更新。

为了高效地求解滑动窗口中的中值，我们可以使用堆数据结构。堆是一种完全二叉树，它具有以下性质：

- 每个节点的值都大于或等于其子节点的值（对于小顶堆）或小于或等于其子节点的值（对于大根堆）。
- 对于任何节点，其左子节点的索引为 2*i+1，右子节点的索引为 2*i+2，其中 i 是该节点的索引。

### 2.2 使用小顶堆和大根堆实现中值计算

为了求解滑动窗口中的中值，我们可以使用一个小顶堆和一个大根堆。小顶堆存储窗口中较大的元素，大根堆存储窗口中较小的元素。

#### 2.2.1 堆的初始化和维护

在初始化时，我们将窗口中的所有元素插入到两个堆中。对于每个元素 x，如果 x 小于当前中值，则将其插入大根堆；否则，将其插入小顶堆。

为了维护堆的性质，每次插入或删除元素后，我们需要调整堆。调整的过程如下：

- **上浮操作：**如果一个节点的值比其父节点的值大（小顶堆）或小（大根堆），则将其与父节点交换，并继续向上比较，直到满足堆的性质。
- **下沉操作：**如果一个节点的值比其子节点的值小（小顶堆）或大（大根堆），则将其与较小的（小顶堆）或较大的（大根堆）子节点交换，并继续向下比较，直到满足堆的性质。

#### 2.2.2 滑动窗口的更新和中值计算

当窗口在数据流中移动时，我们需要更新堆以反映窗口的变化。

- **元素进入窗口：**当一个新的元素进入窗口时，我们将其插入到相应的小顶堆或大根堆中，并调整堆。
- **元素离开窗口：**当一个元素离开窗口时，我们需要从相应的小顶堆或大根堆中删除它。删除操作与插入操作类似，但需要额外的步骤来找到要删除的元素。

中值计算：

- 如果窗口中元素的个数为奇数，则中值是大根堆的堆顶元素。
- 如果窗口中元素的个数为偶数，则中值是大根堆的堆顶元素和小顶堆的堆顶元素的平均值。

### 2.3 算法复杂度分析和优化技巧

使用堆求解滑动窗口中的中值，其时间复杂度为 O(n log k)，其中 n 是数据流中的元素个数，k 是窗口大小。

优化技巧：

- **使用平衡树：**我们可以使用平衡树（如红黑树）来代替堆，以提高插入和删除操作的效率，从而将时间复杂度降低到 O(n log log k)。
- **使用分治算法：**对于非常大的窗口，我们可以使用分治算法将问题分解成更小的子问题，从而降低时间复杂度。
- **使用近似算法：**如果精确的中值计算不是必需的，我们可以使用近似算法，如滑动平均，来降低时间复杂度。

# 3.2 使用堆实现数据流中位数计算

#### 3.2.1 数据流的处理和堆的更新

数据流中位数计算算法的核心思想是使用两个堆：一个小顶堆和一个大根堆。小顶堆存储数据流中较大的那一半元素，而大根堆存储数据流中较小的那一半元素。

当一个新的元素进入数据流时，算法首先将其插入小顶堆。如果小顶堆中的元素个数大于大根堆，则将小顶堆中的最大元素弹出并插入大根堆。这样，小顶堆和大根堆中元素的个数始终保持平衡。

#### 3.2.2 中位数的计算和输出

在任何时刻，如果小顶堆和大根堆中元素的个数相等，则数据流的中位数为小顶堆的最大元素和大根堆的最小元素的平均值。

如果小顶堆中元素的个数比大