优化问题中的矩阵应用：理论与实践


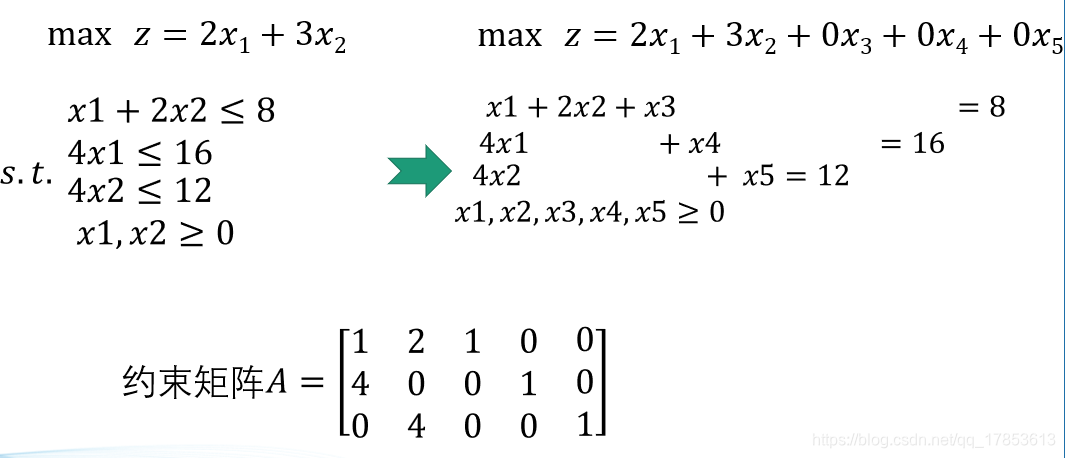
参考资源链接：[《矩阵论》第三版课后答案详解](https://wenku.csdn.net/doc/ijji4ha34m?spm=1055.2635.3001.10343)
# 1. 矩阵理论基础及其在优化问题中的角色

## 1.1 矩阵理论简介

矩阵是一种将数字、符号或表达式排列成矩形阵列的数学工具。在数学、物理学、计算机科学以及工程学中都有广泛的应用，尤其是在解决多变量系统问题时。矩阵理论是线性代数的核心，它为解决线性方程组、线性变换、特征值问题等提供了一套完整的方法论。

## 1.2 矩阵与优化问题的联系

在优化问题中，矩阵常被用作描述系统状态、约束条件和目标函数。通过对矩阵的操作和分析，可以找到满足所有条件的最优解。矩阵的运算特性，比如线性变换的性质，允许我们在高维空间中高效地探索最优解。

## 1.3 矩阵在解决优化问题中的优势

矩阵的向量化操作极大地简化了优化算法的实现。在数据挖掘、机器学习和现代工程设计中，这种向量化方法有效地利用了计算资源，实现了高效率的优化过程。与此同时，矩阵运算的并行化潜力，使得矩阵在处理大数据和大规模优化问题时，拥有得天独厚的优势。

从下一章节开始，我们将深入探讨矩阵运算在不同优化问题中的具体应用和影响。

# 2. 矩阵运算与优化问题

## 2.1 矩阵运算概述

矩阵运算在优化问题中扮演着核心角色，它不仅为表达这些问题提供了强有力的数学工具，而且为寻找解决方案提供了算法基础。这一部分首先介绍矩阵的基本运算，然后分析特殊矩阵在优化问题中的应用。

### 2.1.1 矩阵的基本运算

矩阵运算包括加法、减法、数乘、矩阵乘法以及矩阵的转置等。这些基本运算构成了矩阵理论的基石，并且在优化算法的设计与实现中至关重要。

#### 矩阵加法与减法
对于同型矩阵A和B，矩阵加法定义为对应元素相加。矩阵减法则是对应元素相减。用数学符号表示，如果A和B是m×n的矩阵，那么它们的和C=A+B也是一个m×n的矩阵，其元素由c_ij=a_ij+b_ij给出。

#### 数乘
数乘是指矩阵与一个标量的乘积，即每个元素都乘以这个标量。

#### 矩阵乘法
矩阵乘法是较为复杂的运算，其定义如下：如果A是一个m×n的矩阵，B是一个n×p的矩阵，那么C=A×B是一个m×p的矩阵，其元素由c_ij=∑a_ik*b_kj（对所有k从1到n求和）给出。

#### 矩阵的转置
矩阵A的转置，记作A^T，是将矩阵A的行换成列得到的矩阵。如果A是一个m×n的矩阵，那么A^T就是一个n×m的矩阵。

这些基本运算在优化问题中经常出现，例如在线性规划问题中，矩阵乘法常用于构建目标函数和约束条件。

### 2.1.2 特殊矩阵与优化问题

在优化问题中，特殊矩阵常常出现在特定的算法和应用场景中。比如单位矩阵、对角矩阵、稀疏矩阵等。

#### 对角矩阵
对角矩阵是一种特殊的方阵，其非对角线上的元素全部为0。在优化问题中，对角矩阵因其计算的简便性而被广泛使用。

#### 稀疏矩阵
稀疏矩阵是一种大部分元素为0的矩阵，在大型优化问题中非常常见。它们在存储和运算中能够显著减少资源消耗。

#### 单位矩阵
单位矩阵是主对角线上的元素全为1，其余位置的元素全为0的方阵。单位矩阵在算法中起到“恒等变换”的作用。

## 2.2 矩阵分析与优化算法

### 2.2.1 矩阵特征值与特征向量

矩阵的特征值与特征向量是理解线性变换和矩阵性质的关键。对于一个n×n的方阵A，如果存在非零向量v和标量λ使得Av=λv，则称v为A的一个特征向量，λ为对应的特征值。

#### 计算特征值和特征向量

通常计算特征值和特征向量可以通过求解特征方程|A-λI|=0得到，其中I是单位矩阵，特征向量可以通过解线性方程(A-λI)v=0得到。

import numpy as np

# 定义一个矩阵
A = np.array([[4, 2], [1, 3]])

# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)

print("特征值: ", eigenvalues)
print("特征向量: \n", eigenvectors)

### 2.2.2 奇异值分解与优化问题

奇异值分解（SVD）是另一种重要的矩阵分解技术，在优化问题中有着广泛的应用。对于一个m×n的矩阵A，SVD将其分解为A=UΣV^T，其中U和V是正交矩阵，Σ是对角矩阵，其对角线上的元素是A的奇异值。

#### 应用奇异值分解

奇异值分解不仅可以用于矩阵的低秩近似，而且在数据压缩、特征提取和系统识别等领域都有应用。

# 定义一个矩阵
A = np.array([[1, 2, 3], [4, 5, 6]])

# 进行奇异值分解
U, s, Vt = np.linalg.svd(A)

print("U 矩阵: \n", U)
print("奇异值向量: ", s)
print("V 矩阵的转置: \n", Vt)

## 2.3 矩阵运算的数值稳定性

在计算机进行矩阵运算时，由于有限的计算精度，会出现数值误差，所以需要采取措施来提高数值稳定性。

### 2.3.1 矩阵运算中的数值误差

数值误差主要由浮点数运算的精度限制和舍入误差引起。例如，矩阵乘法在数值运算中可能会放大误差。

### 2.3.2 提高数值稳定性的策略

为了提高数值稳定性，可以采取如下策略：

- 使用稳定的数学库进行运算，如LAPACK或BLAS。
- 利用矩阵的特性进行优化，比如对称矩阵、正定矩阵等。
- 对于一些特殊矩阵，可以使用专门的分解技术（如Cholesky分解、LU分解）来减少运算误差。

# 使用NumPy的矩阵乘法可以保证数值稳定性
import numpy as np

# 定义两个矩阵
A = np.array([[1, 2], [3, 4]], dtype=np.float64)
B = np.array([[5, 6], [7, 8]], dtype=np.float64)

# 进行稳定的矩阵乘法运算
C = np.dot(A, B)

print("运算结果: \n", C)

以上章节中，我们探究了矩阵运算的基础及其在优化问题中的应用，从基本运算到特殊矩阵的性质分析，再到如何处理数值稳定性的问题。这些内容不仅为后续章节中线性规划和非线性优化的深入讨论打下了基础，也为实际应用提供了理论与技术指导。

# 3. 矩阵在线性规划中的应用

## 3.1 线性规划基础与矩阵表示

### 3.1.1 线性规划问题的定义

线性规划是研究在给定一组线性不等式约束条件下，如何优化（最大或最小化）一个线性目标函数的问题。这类问题在资源分配、生产规划、物流配送等领域有着广泛的应用。线性规划问题可以用以下数学模型来描述：

设目标函数为：
\[ \text{maximize/minimize} \quad \mathbf{c}^T \mathbf{x} \]

约束条件为：
\[ \mathbf{Ax} \leq \mathbf{b} \]
\[ \mathbf{x} \geq 0 \]

其中，\( \mathbf{c} \) 是目标函数系数向量，\( \mathbf{x} \) 是决策变量向量，\( \mathbf{A} \) 是约束系数矩阵，\( \mathbf{b} \) 是约束条件值向量。

### 3.1.2 线性规划的矩阵形式

线性规划问题的矩阵形式提供了一种简洁且便于计算的方式来表达问题。矩阵形式不仅能够清晰地展示问题的结构，还能够利用矩阵运算高效地解决问题。将线性规划的原始模型转化为矩阵形式，可以表示为：

\[ \text{maximize/minimize} \quad \mathbf{c}^T \mathbf{x} \]
\[ \text{subject to} \quad \mathbf{A} \mathbf{x} = \mathbf{b} \]
\[ \mathbf{x} \geq 0 \]

这里，决策变量向量 \( \mathbf{x} \) 包含了所有需要确定的变量，目标函数向量 \( \mathbf{c} \) 中的每个元素对应一个目标函数系数，约束系数矩阵 \( \mathbf{A} \) 和向量 \( \mathbf{b} \) 定义了问题的约束条件。

### 3.1.3 线性规划问题的矩阵表示和求解优势

采用矩阵形式表示线性规划问题的优势在于：

- 简洁性：矩阵符号可以大大简化问题的书写。
- 可视化：矩阵形式便于问题的可视化和理解。
- 计算效率：利用矩阵运算可以提高线性规划问题的求解效率。
- 软件实现：多数线性规划软件包和库都支持以矩阵形式输入问题，如MATLAB、Lingo、Gurobi等。

通过矩阵表示线性规划问题，研究者和工程师可以更方便地对问题进行分析和求解，这对于解决实际问题具有重要意义。

## 3.2 简化和变换线性规划问题

### 3.2.1 矩阵操作简化线性规划问题

矩阵操作在简化线性规划问题中扮演了重要角色。使用矩阵运算可以将多个约束条件合并，减少变量的数量，或者转换为标准形式。例如，通过初等行变换，可以将约束矩阵 \( \mathbf{A} \) 转换为简化行阶梯形式，进而找到基可行解，并构建单纯形法所需的初始单纯形表。

### 3