模型预测控制vs PID控制：MATLAB深度分析与比较

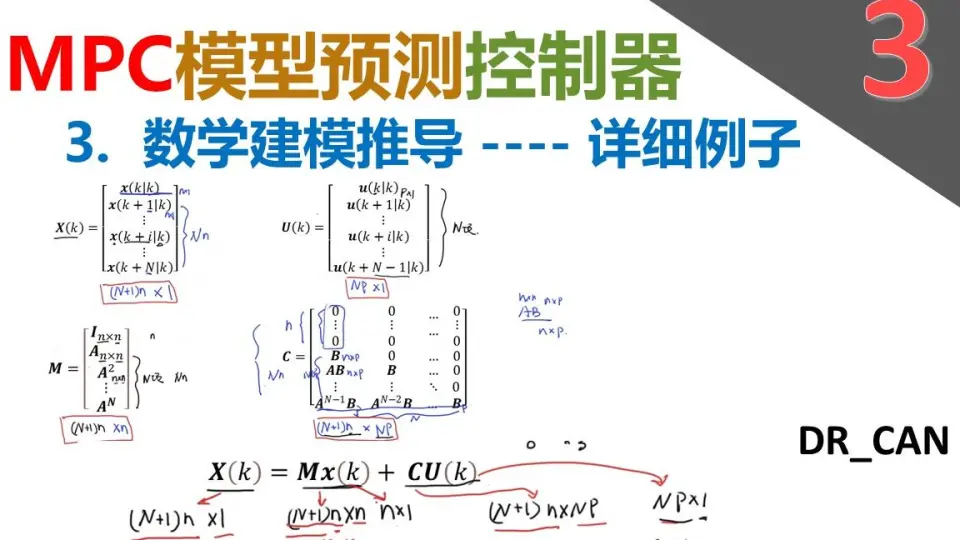
# 1. 模型预测控制与PID控制的基本概念

## 概述

模型预测控制（MPC）和比例-积分-微分（PID）控制是现代控制系统中广泛使用的两种策略。MPC是一种先进的控制算法，它利用过程模型来预测未来的行为，并进行优化以满足设定目标。相比之下，PID控制器是一种历史悠久的控制策略，基于过程的当前误差来调整控制动作。

## 模型预测控制与PID控制的区别

尽管两者都是为了改善系统的响应和性能，但它们在操作原理、实现方式和应用范围上存在显著差异。MPC能够处理多变量系统的约束问题，并且优化未来一段时域内的系统表现，而PID控制则侧重于即时的误差调整，并不直接考虑未来的系统状态。在实际应用中，选择哪一种控制策略，需要根据系统的具体需求和特点来定。

## 应用环境与选择依据

MPC特别适合于有明显未来行为预测需求的复杂动态系统，例如化工过程、航天飞行器控制等。PID控制因其简单易实现和良好的鲁棒性，在温度控制、速度控制等领域得到广泛应用。通过理解这两种控制策略的基本概念，可以帮助工程师在不同情况下作出明智的选择。

# 2. 模型预测控制理论与实践

## 2.1 模型预测控制基础理论

### 2.1.1 模型预测控制的定义

模型预测控制（MPC）是一种先进的过程控制策略，它结合了优化技术和反馈控制。MPC的核心在于通过一个过程模型预测未来的输出，并优化未来的控制动作来达到期望的输出。在MPC中，控制动作是通过解决一个在线优化问题得到的，该问题包括了对未来输出的预测以及对控制策略的限制。这种控制策略特别适用于处理多变量控制问题、有约束的过程以及复杂动态系统。

### 2.1.2 模型预测控制的工作原理

模型预测控制的工作原理可以分为以下几个关键步骤：

1. **模型预测**：根据当前系统的状态和控制输入，利用数学模型预测未来一段时间内系统的输出。
2. **优化问题求解**：设定一个成本函数，通常为未来输出误差的加权和，以及控制动作变化的加权和。通过解决一个在线优化问题来最小化这个成本函数。
3. **控制动作的实现**：从优化求解结果中取第一个控制动作应用到系统中。
4. **反馈校正**：在下一个采样周期，利用新的测量值更新系统状态，并重复预测和优化步骤。

这一过程持续进行，确保了控制策略能够适应模型不确定性和外部扰动的影响，从而改善整个控制过程的性能。

## 2.2 模型预测控制的MATLAB实现

### 2.2.1 系统模型的构建

在MATLAB环境下，实现MPC首先需要构建一个准确的系统模型。这可以通过MATLAB的系统识别工具箱来完成，也可以直接根据系统的物理知识建立数学模型。MATLAB支持多种模型表达方式，如传递函数（Transfer Function）、状态空间模型（State Space Model）和脉冲响应模型（Impulse Response Model）等。

% 以传递函数为例，构建一个简单的一阶系统模型
num = 1;    % 分子参数
den = [1, 2]; % 分母参数
sys = tf(num, den); % 创建传递函数模型

### 2.2.2 预测模型的创建与优化

在MATLAB中，MPC控制器的创建和优化是使用Model Predictive Control Toolbox来完成的。设计MPC控制器时，需要设定预测范围、控制范围以及权重参数等。

% 创建MPC控制器
MPC_controller = mpc(sys, Ts, PredictionHorizon, ControlHorizon);

其中`Ts`是采样时间，`PredictionHorizon`和`ControlHorizon`分别是预测范围和控制范围。MPC控制器的参数，如权重、约束等，都可以通过`set`函数进行调整。

### 2.2.3 控制器设计与仿真分析

创建MPC控制器后，需要在MATLAB中进行仿真分析，以验证控制器的性能。仿真可以通过模拟不同工况和扰动来观察系统的响应。

% 设定仿真时间
T = 100;
% 创建模拟器
Simulator = mpcsim(MPC_controller, T);
% 运行仿真
[~,~,~,mpcinfo] = Simulator.simulate;

以上代码利用`mpcsim`函数创建了一个模拟器，并进行仿真。`mpcinfo`变量中包含了仿真过程中的详细信息，可以用于进一步分析控制器性能。

## 2.3 模型预测控制的进阶应用

### 2.3.1 非线性系统预测控制

模型预测控制在处理非线性系统时，通常采用对非线性模型进行线性化或者使用非线性优化技术。在MATLAB中，可以利用MPC工具箱内置的非线性MPC模块来实现。

% 假设非线性模型已知
nonlinearModel = ... ; % 非线性系统模型描述

% 创建非线性MPC控制器
nmcontroller = nlmpc(nonlinearModel);

### 2.3.2 多变量预测控制策略

在多变量系统中，MPC需要同时控制多个输入和输出变量。MATLAB提供了一个灵活的框架来定义和解决多变量MPC问题。

% 定义多变量MPC控制器
MPC_controller = mpc(sys, Ts);
MPC_controller.MV = struct('Min',MVmin,'Max',MVmax); % 定义输入变量的约束
MPC_controller.OV = struct('Min',OVmin,'Max',OVmax); % 定义输出变量的约束

% 优化控制器参数
set(MPC_controller,'Weights.OutputVariables',1);
set(MPC_controller,'Weights.ManipulatedVariablesRate',0.1);

以上代码对多变量MPC控制器的输入和输出变量进行了约束，并设置了相应的权重参数。

通过以上各节的讨论，我们能够看到模型预测控制理论的深奥和实现上的实用性。在下一章节中，我们将详细探讨PID控制理论与实践，并与模型预测控制进行对比。

# 3. PID控制理论与实践

## 3.1 PID控制基础理论
### 3.1.1 PID控制器的组成
PID控制器（比例-积分-微分控制器）是最常见的反馈回路控制器之一，其组成包括比例（Proportional）、积分（Integral）、微分（Derivative）三个基本控制部分。比例部分负责减少系统的瞬时误差，积分部分负责消除静差，消除累积误差，而微分部分则负责预测系统未来的行为，通过当前误差变化率来对系统进行校正。这三部分共同工作，使得控制器能够对系统性能进行有效控制。

### 3.1.2 PID控制算法的原理
PID控制算法的基础在于计算误差值，即设定值（Setpoint，SP）与过程变量（Process Variable，PV）之间的差值。该算法原理可以表示为：

\[ u(t) = K_p \cdot e(t) + K_i \cdot \int_{0}^{t} e(t) dt + K_d \cdot \frac{de(t)}{dt} \]

其中，\( u(t) \)是控制器输出，\( e(t) \)是误差值，\( K_p \)、\( K_i \)和\( K_d \)分别是比例、积分和微分的增益系数。该方程从数学上描述了如何综合三个控