矩阵的逆：求解和应用，解决线性方程组的利器

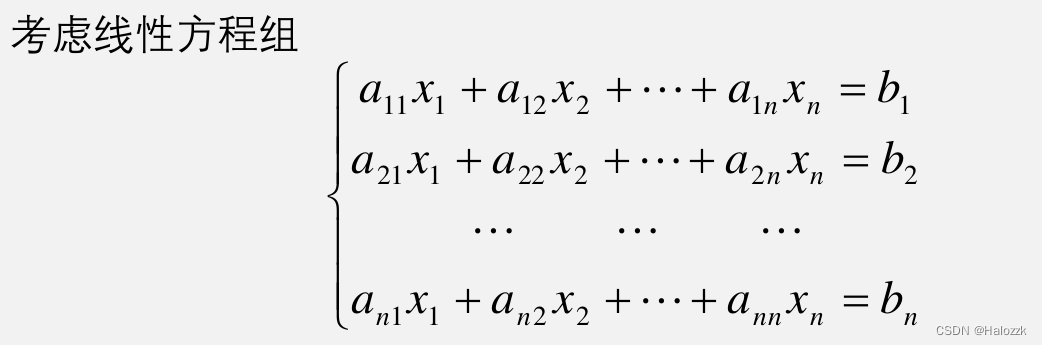
# 1. 矩阵的逆：概念和求解方法

矩阵的逆是线性代数中一个重要的概念，它表示一个矩阵的可逆性，并允许我们求解线性方程组。

### 1.1 矩阵逆的定义

对于一个 n×n 方阵 A，如果存在一个 n×n 方阵 B，使得 AB = BA = I（单位矩阵），则称 A 为可逆矩阵，B 为 A 的逆矩阵，记作 A^-1。

### 1.2 矩阵逆的性质

* **唯一性：**如果 A 是可逆矩阵，则其逆矩阵唯一。
* **乘法逆：**对于可逆矩阵 A，(A^-1)^-1 = A。
* **转置逆：**如果 A 是可逆矩阵，则 (A^-1)^T = (A^T)^-1。

# 2. 线性方程组的求解

### 2.1 线性方程组的表示和求解

线性方程组是一组线性方程，形式为：

a11x1 + a12x2 + ... + a1nxn = b1
a21x1 + a22x2 + ... + a2nxn = b2
am1x1 + am2x2 + ... + amnxn = bm

其中，aij 表示系数矩阵 A 的元素，xi 表示未知数，bi 表示常数项。

求解线性方程组的方法有多种，其中一种方法是使用矩阵逆。

### 2.2 矩阵逆在求解线性方程组中的应用

如果系数矩阵 A 是可逆的，则线性方程组有唯一解，可以用矩阵逆求解：

X = A^-1 * B

其中，X 是未知数列向量，B 是常数项列向量。

**代码块：**

import numpy as np

# 系数矩阵
A = np.array([[1, 2], [3, 4]])

# 常数项列向量
B = np.array([5, 6])

# 求解矩阵逆
A_inv = np.linalg.inv(A)

# 求解未知数列向量
X = np.dot(A_inv, B)

print(X)

**逻辑分析：**

* 使用 NumPy 库的 `linalg.inv()` 函数求解矩阵逆。
* 使用 NumPy 的 `dot()` 函数计算矩阵乘法。
* 输出求解的未知数列向量。

**参数说明：**

* `A`：系数矩阵
* `B`：常数项列向量
* `A_inv`：矩阵逆
* `X`：未知数列向量

### 2.3 矩阵逆的应用实例

矩阵逆在求解线性方程组中有着广泛的应用，例如：

* **物理学：**求解力学、电磁学等领域的线性方程组。
* **计算机图形学：**求解变换矩阵、投影矩阵等。
* **统计学：**求解回归模型的系数。

**表格：**

| 应用领域 | 线性方程组示例 |
|---|---|
| 物理学 | 求解牛顿第二定律 |
| 计算机图形学 | 求解旋转矩阵 |
| 统计学 | 求解线性回归模型 |

# 3.1 矩阵逆的定义和性质

**定义**

矩阵逆，也称为乘法逆或代数余子式矩阵，是对于给定可逆矩阵 A，存在一个矩阵 B，使得 AB = BA = I，其中 I 是单位矩阵。

**性质**

* **唯一性：**如果矩阵 A 可逆，则其逆矩阵唯一存在。
* **可逆矩阵的性质：**可逆矩阵的行列式不为零，且其秩等于矩阵的阶数。
* **逆矩阵的性质：**逆矩阵的转置等于其自身的逆矩阵，即 (A^-1)^T = A^-1。
* **行列式的逆：**可逆矩阵 A 的行列式 det(A) 不为零，且 det(A^-1) = 1/det(A)。
* **逆