【排序优化秘籍】：希尔排序时间复杂度的革命性改进

# 1. 希尔排序概述与历史背景

## 1.1 排序算法的演变
在计算机科学早期，排序算法是数据处理的重要组成部分。随着时间的推移，算法的发展经历了从简单到复杂的演变过程。从冒泡排序到快速排序，每一步都体现了对效率和速度的不懈追求。

## 1.2 希尔排序的诞生
希尔排序由计算机科学家Donald Shell于1959年提出，旨在提高插入排序在处理大规模数据时的效率。它通过将数据集分组并分别进行插入排序，最终合并成一个有序的数据集，从而减少排序的总步骤数。

## 1.3 历史意义与影响
希尔排序的出现，为排序算法的发展注入了新的活力。尽管在后来涌现出许多更高效的排序算法，但希尔排序因其简单性和一定的适用性，仍然在特定场合发挥着重要作用。随着对算法效率和优化需求的增长，对其深入研究与应用仍在继续。

# 2. 希尔排序核心算法解析

### 2.1 希尔排序基础概念
#### 2.1.1 希尔排序的定义与原理
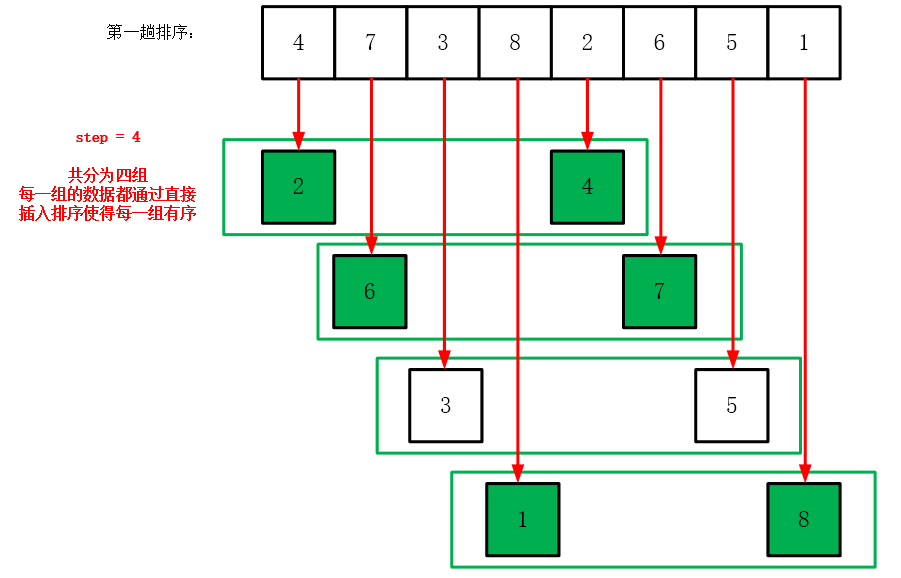
希尔排序（Shell Sort）是一种基于插入排序的算法，通过将原始数据分成若干个子序列，分别进行直接插入排序，使得原始数据基本有序，最后再对全体记录进行一次直接插入排序。希尔排序是针对直接插入排序的低效性，尤其是在处理大规模数据时，通过分治的策略提高效率。该算法由Donald Shell在1959年提出。

希尔排序的核心思想是将数据分组进行插入排序，组间数据的相对位置会产生变化，但组内数据基本保持不变。这样做的好处是，每次对各个组进行插入排序后，整个序列的“部分有序”程度会更高。之后再对整个序列进行一次插入排序时，由于数据已经接近有序，插入排序的效率会大大提升。

希尔排序可以被看作是一种“缩小增量排序”，其增量序列的选择至关重要，直接关系到算法的效率。最简单的增量序列是`n/2, n/4, ..., 1`，但是更复杂的增量序列可以带来更好的性能表现。

#### 2.1.2 希尔排序与传统排序算法的对比
相比于传统的插入排序，希尔排序的显著优势在于其能够处理更大规模的数据集，且时间复杂度优于直接插入排序。在最坏的情况下，插入排序的时间复杂度是`O(n^2)`，而希尔排序的平均时间复杂度可以达到`O(nlogn)`或`O(nlog^2n)`。希尔排序并不保证是稳定的排序方法，也就是说，它可能会改变相等元素的相对位置。

在实际应用中，希尔排序经常用于对部分有序的数据进行排序，或者与其他排序算法结合使用。例如，在快速排序的分区操作之前，先用希尔排序进行预处理，可以减少分区的范围，从而提高整体效率。

### 2.2 希尔排序关键步骤详细分解
#### 2.2.1 初始间隔的确定方法
选择合适的初始间隔是希尔排序算法的关键。初始间隔`gap`的选取对算法的效率影响很大。一个常用的策略是使用Hibbard增量序列，即`1, 3, 7, 15, ...`，也可以采用Knuth提出的增量`1, 4, 13, ...`。增量序列可以是固定的，也可以是动态计算出来的。

#### 2.2.2 插入排序的变种实现
希尔排序的每一轮可以看作是一种特殊的插入排序过程，其在排序时使用的是增量`gap`而不是`1`。在每个间隔`gap`上进行的插入排序，将数组分割成若干个间隔为`gap`的子数组，并独立地对每个子数组进行插入排序。这一步骤确保了在整体排序过程中，大的间隔首先被缩小，小的间隔随后进一步调整，从而逐步逼近最终的有序状态。

#### 2.2.3 间隔序列的选择与优化
间隔序列的选择至关重要，它决定了算法的效率。一个理想的间隔序列应当从一个较大的数开始，然后递减到`1`，并且间隔序列的每个数最好是互质的。选择间隔序列的一种方法是使用序列`n/2, n/4, ..., 1`，其中`n`是数组的长度。然而，通过研究，人们已经发现更高效的间隔序列，例如Hibbard增量序列或者Sedgewick增量序列`1, 5, 19, 41, 109, ...`。

### 2.3 算法时间复杂度分析
#### 2.3.1 最坏、平均和最好情况的时间复杂度
希尔排序的时间复杂度与间隔序列的选择密切相关。在最坏的情况下，即输入序列完全逆序时，希尔排序的时间复杂度为`O(n^2)`。但是，在实际使用中，由于初始间隔的存在，希尔排序的效率通常会比直接插入排序要高。

在平均情况下，时间复杂度可以达到`O(nlogn)`或者`O(nlog^2n)`，具体取决于间隔序列的选择。而最好的情况，即输入序列本身已经部分有序时，时间复杂度可以降至`O(n)`。

#### 2.3.2 理论分析与实际运行时间对比
理论上的时间复杂度分析提供了希尔排序性能的参考。在实际应用中，运行时间还会受到计算机硬件、数据分布模式以及间隔序列选择的影响。因此，实验测试是在实际应用中了解希尔排序性能的重要手段。在实际的数据集上进行测试，可以更准确地评估算法的性能。

希尔排序的性能优化空间较大，通过合理选择间隔序列和优化代码实现，可以在很多实际场景中提升算法的运行效率。在对数据进行预处理或者作为其他复杂排序算法的子过程时，希尔排序可以扮演重要的角色。

# 3. 希尔排序性能优化实践

希尔排序作为基于插入排序的一种高效算法，通过适当的间隔序列调整，可以显著提升排序性能。优化策略的探索和代码实现的改进不仅对希尔排序本身是重要的，也对理解和实现其他排序算法提供了宝贵的参考。

## 3.1 优化策略与技巧

### 3.1.1 间隔序列的调整策略

间隔序列的选择对希尔排序的性能至关重要。经典的间隔序列选择方法是使用希尔初始序列，即数组的长度除以2，但之后每次再除以2。然而，这种简单的序列可能会导致排序过程中出现效率瓶颈。因此，更优的间隔序列选择策略被不断提出，比如通过数值分析来获得更优间隔序列，以及使用更复杂的数学公式来调整间隔序列。

**间隔序列选择的优化