C++实现数据结构：二叉搜索树与AVL树的构建与操作

"数据结构用C++描述，包含二叉搜索树、AVL搜索树、B-树和散列及冲突解决的理论与实践题目解答" 在数据结构中，C++是一种常用的语言来实现各种数据结构。本资料主要关注的是二叉搜索树、AVL树、B-树以及散列表等概念，这些都是计算机科学中基础且重要的数据结构。 1. 二叉搜索树（BST）是一种特殊的二叉树，其中每个节点的左子树只包含小于该节点的元素，右子树包含大于该节点的元素。问题要求建立给定数字的二叉搜索树，并模拟删除过程，这涉及到了BST的插入和删除操作。例如，删除操作通常包括找到待删除节点，然后根据其子节点情况调整树的结构以保持二叉搜索树的性质。 2. 判断一个给定的二叉树是否为二叉搜索树的算法如题所示，通过递归检查每个节点的元素值是否满足BST的条件。如果在遍历过程中发现不满足条件，算法将设置`fail`标志为true，表示该树不是二叉搜索树。 3. AVL树是自平衡的二叉搜索树，要求左右子树的高度差不超过1。构建AVL树的过程涉及到旋转操作，以保持树的平衡。题目提供了两个序列，要求从空树开始构造AVL树，这需要理解AVL树的插入规则和平衡因子的概念。 4. B-树是一种多路搜索树，适用于大容量存储系统，如磁盘。问题探讨了5阶B-树的高度和元素数量的关系，以及如何构建B-树。B-树的高度决定了查找效率，而元素个数则影响到树的分支因子和平衡状态。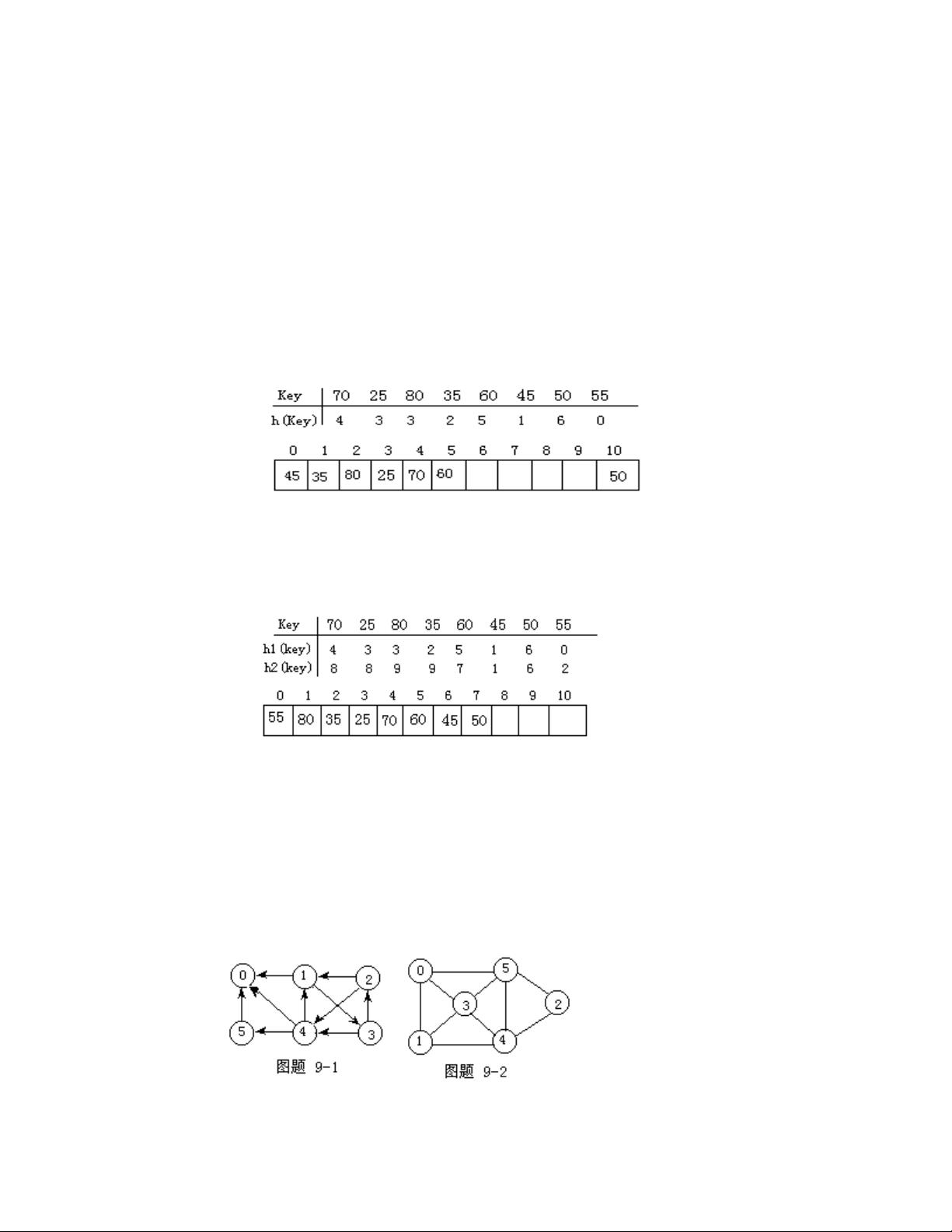 5. 散列是快速查找的关键技术，通过散列函数将关键字映射到数组位置。线性探查和拉链法是常见的冲突解决策略。在给定的题目中，需要建立散列表并处理冲突，同时给出了拉链法解决冲突的C++函数实现。在散列表中，搜索操作通常非常高效，因为可以通过直接计算索引来访问。 这些题目涵盖了数据结构中的核心概念，包括二叉搜索树的构建和操作、自平衡树的构建、B-树的构造和操作，以及散列查找和冲突解决。理解和掌握这些内容对于深入学习计算机科学和提升编程能力至关重要。