线性控制系统稳定性与稳态误差分析
版权申诉
155 浏览量
更新于2024-07-08
收藏 2.83MB PPT 举报
"该PPT主要讲解了自动控制理论中的第四章内容——稳定性和稳态误差。内容包括线性系统稳定性的基本概念、基于传递函数的系统稳定性判定以及与Routh判据相关的稳定性分析方法。此外,也提到了俄国数学家李雅普诺夫在稳定性分析领域的贡献。"
在自动控制理论中,稳定性是评价一个控制系统性能好坏的关键因素。当外部扰动或内部参数变化时,一个稳定的系统能够自我调整并保持在期望的工作状态附近。如果系统不稳定,它可能会发生振荡或无法回到其原始状态,导致控制失效。
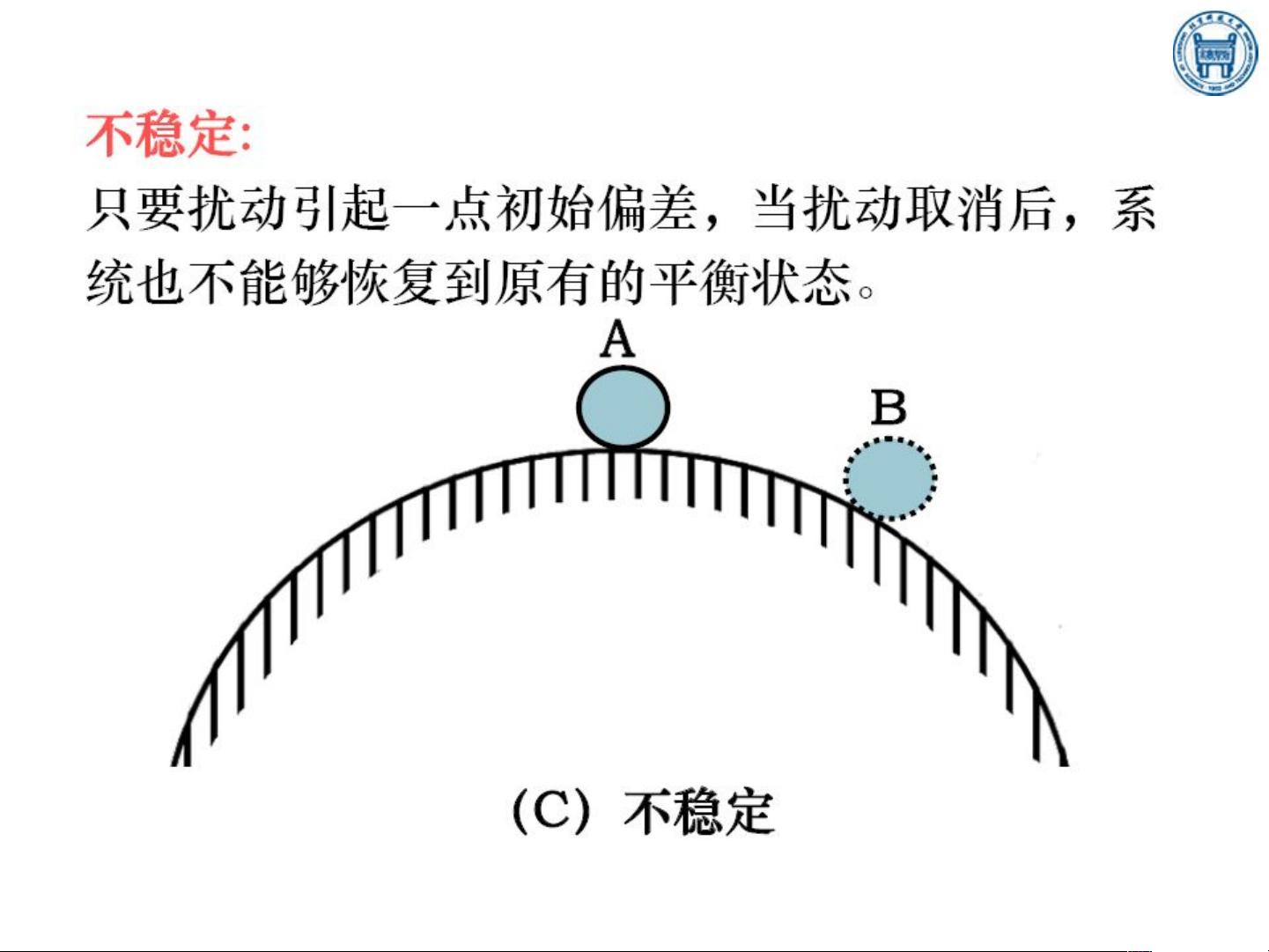
4.1线性系统稳定性的基本概念:
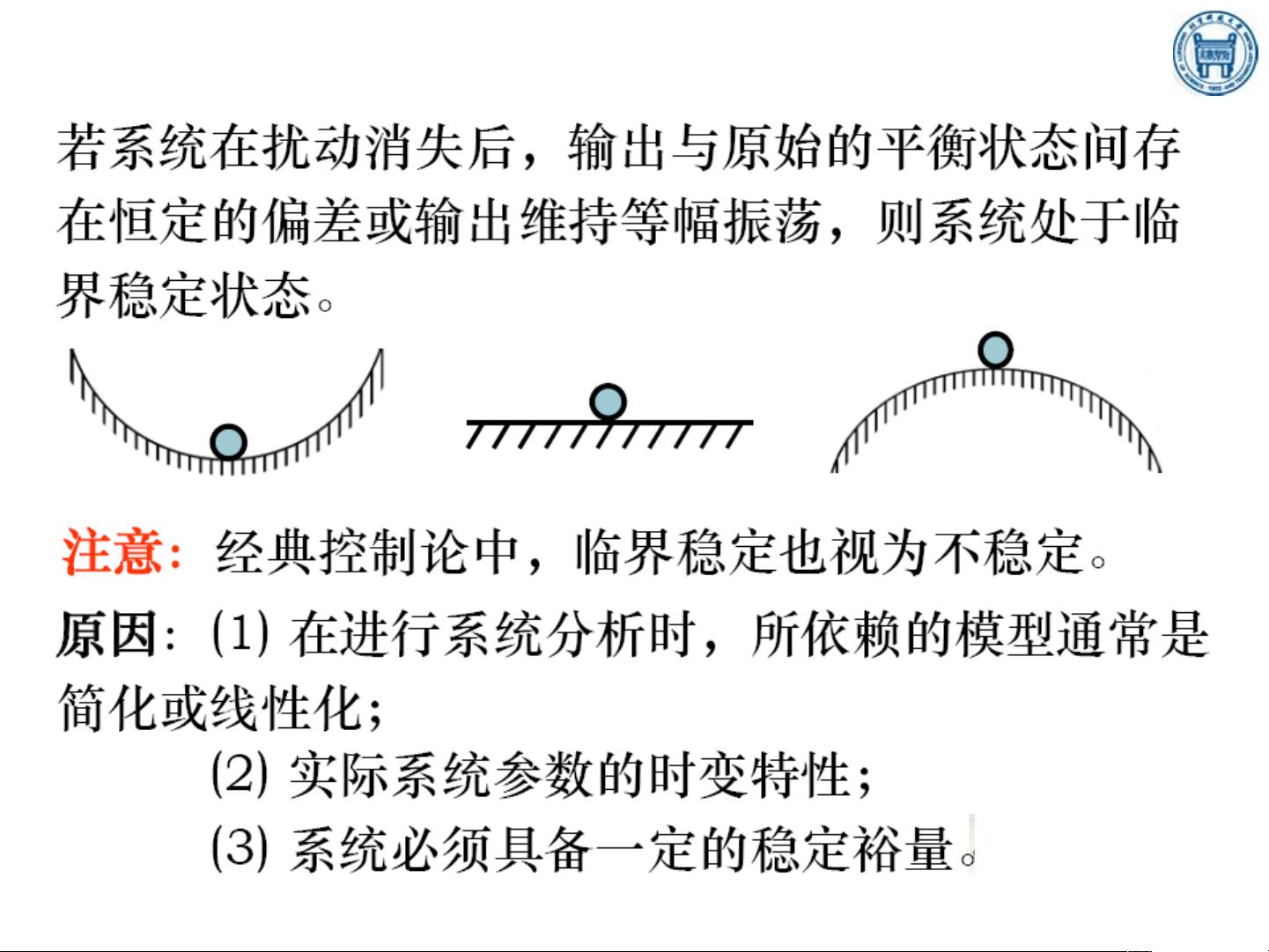
系统稳定性有多种定义,但基本思想是系统在受到扰动后,能否逐渐回到其原有的平衡状态。这个过程可以分为两个方面:渐近稳定和李雅普诺夫稳定性。渐近稳定意味着系统在扰动后能无限接近原来的平衡点;而李雅普诺夫稳定性则通过研究系统的状态变量来判断系统的稳定性,即如果系统状态变量的绝对值在任意小的邻域内都能保持不变,则系统是稳定的。
4.2传递函数表示的系统稳定性判定:
对于单输入单输出(SISO)线性定常系统,可以通过传递函数来分析稳定性。Routh判据是一种常用的工具,它基于系统的闭环特征方程的系数来决定系统的稳定性。当特征方程的所有正根都位于复平面上的左半平面时,系统是稳定的。
4.2.1 SISO线性定常系统的稳定性:
稳定性分析通常涉及到系统的动态响应,特别是当系统受到外部扰动或内部参数变化时的行为。平衡状态是系统不受外力作用时的静止状态。如果系统在扰动后能从平衡状态的偏离逐渐恢复,那么它是稳定的。
4.2.2 Routh稳定判据:
Routh判据是一种代数方法,通过构造Routh-Hurwitz阵列来检查特征方程的根,从而确定系统是否稳定。如果所有主对角线上的元素都是正的,并且次对角线上的元素按顺序交替符号,那么系统是稳定的。
4.2.3和4.2.4 Routh判据的特殊情况和推广:
Routh判据有几种特殊情况,如当特征方程存在纯虚根时的处理,以及如何将该方法扩展到多变量和非最小相位系统。这些推广使得Routh判据成为一种广泛应用的稳定性分析工具。
自动控制理论中的稳定性分析是理解和设计控制器的基础,它确保系统在各种条件下的可靠运行,避免失控或性能下降。李雅普诺夫的稳定性理论为此提供了坚实的理论基础,并对现代控制理论的发展产生了深远影响。通过掌握这些基础知识,工程师可以有效地评估和改进控制系统的性能。
215 浏览量
2021-12-04 上传
2021-12-04 上传
2022-06-27 上传
2021-10-05 上传
2021-12-04 上传
2021-12-04 上传
2022-07-07 上传
2022-07-07 上传
等天晴i
- 粉丝: 5982
- 资源: 10万+
最新资源
- C#窗体编程-----------.doc
- linux 内存寻址
- 计算机的常用网络命令
- 计算机组成原理与系统结构实验教程
- Liunx文件系统基本目录介绍说明
- Linux必学60个命令文件处理
- 8101E 安装说明
- SQL2008 Upgrade Technical Reference Guide
- DIV+CSS布局大全
- BTS3900WCDMA硬件安装指南
- C#教程(PDF格式)
- 高等代数各章节课件多项式.行列式.线性方程等等
- GPU_Programming_基于GPU编程的中文文档
- 海量数据访问——示例(C++)
- flexflexflexflexflexflex
- 长波授时系统相位跟踪点检测的数字化研究