Python线性回归分析：jupyter notebook实现待定系数与R2详解

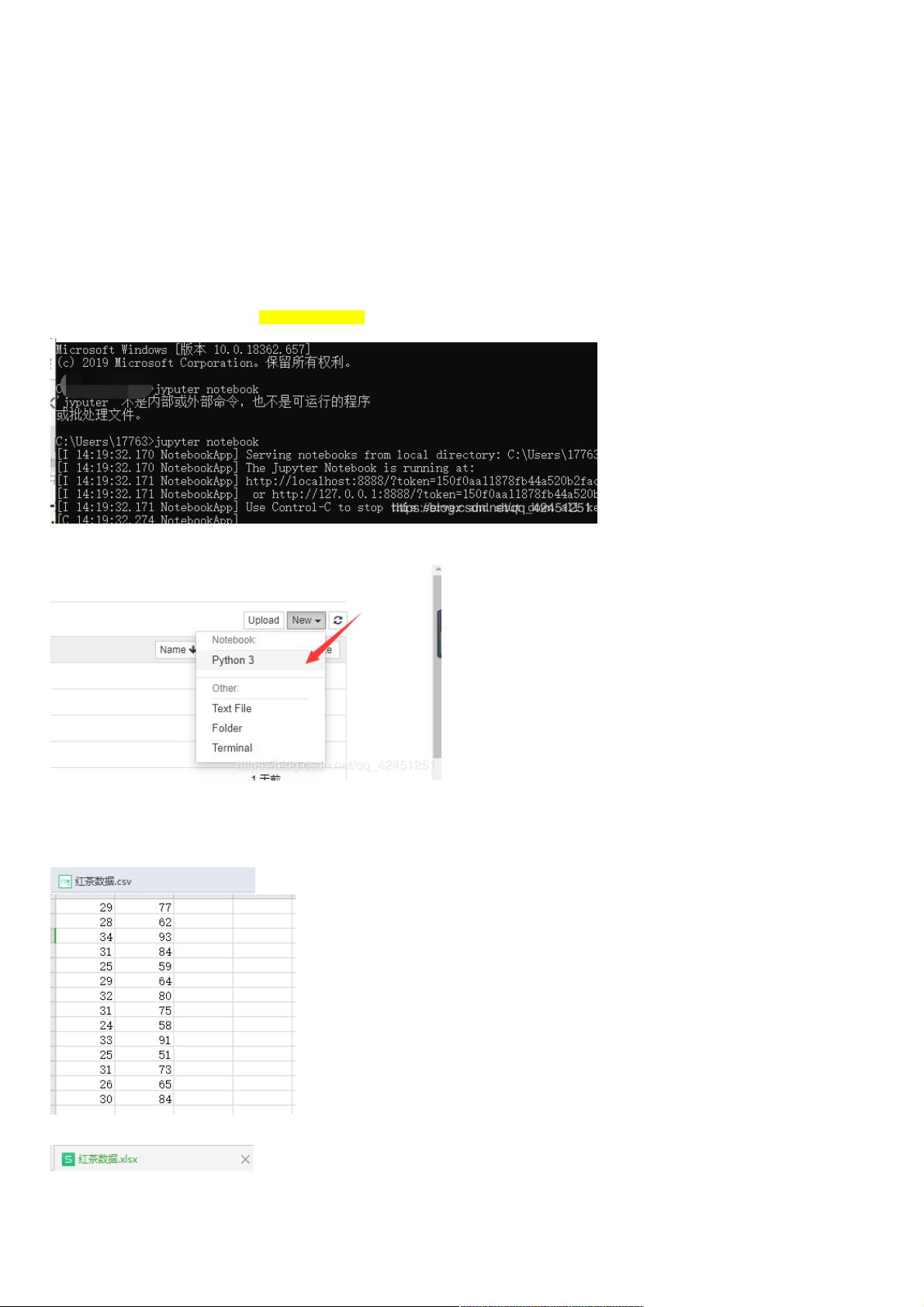
"这篇教程将指导读者如何使用Jupyter Notebook进行Python编程，特别是解决线性回归方程中的待定系数a和判定系数R²。通过详细的步骤，文章旨在帮助读者理解线性回归方程的计算过程，而不仅仅是依赖于第三方库。" 线性回归是一种统计分析方法，用于研究两个或多个变量之间的线性关系。在这个教程中，我们将使用Python编程语言，结合Jupyter Notebook这一交互式开发环境来分析和求解线性回归方程。Jupyter Notebook是一个开源工具，它允许用户以文档形式编写和运行代码，非常适合数据分析和教学。 首先，我们需要运行Jupyter Notebook。在Windows操作系统中，可以通过打开命令行终端并输入`jupyter notebook`来启动这个工具。启动后，会显示一个Web界面，我们可以在其中创建新的Python文件。 在Python环境中，处理线性回归问题通常需要导入一些关键库，例如`numpy`（用于数值计算）和`pandas`（用于数据处理）。教程中提到的数据可能是存储在表格格式的数据集，如CSV文件，我们需要先加载这些数据。 接着，我们将为自变量（例如温度）和因变量（例如销售量）赋值。然后，计算自变量和因变量的均值，这是分析的基础。离差平方和（如温度与平均温度之差的平方和，销售量与平均销售量之差的平方和）以及离差积和（温度与平均温度之差乘以销售量与平均销售量之差的总和）是计算回归系数的关键。 通过离差平方和，我们可以计算回归方程的系数a和截距b，从而得到线性回归方程y = ax + b。有了这个方程，我们可以预测任意温度下的销售量，即计算出预测值sales1。进一步，我们需要计算预测值的平均值y2，预测销售值与预测销售平均值的离差平方和，以及实际值（销售值y）与预测值（sales1）的离差积和。 判定系数R²是评估模型拟合优度的重要指标，它表示了模型解释变量变化的百分比。R²的计算涉及到预测值与实际值的差异（Se），R²等于1 - Se / Sy，其中Sy是因变量的离差平方和。此外，还有一种不同的计算R²的方法。 最后，为了可视化结果，我们可以绘制线性回归曲线，并使用seaborn库添加置信带，这有助于理解数据的波动范围和模型的不确定性。 这个教程深入浅出地讲解了如何在Jupyter Notebook中手动实现线性回归分析，强调了理解每个步骤的重要性，这对于提升数据分析技能和独立解决问题的能力非常有帮助。通过实践这些步骤，读者不仅能学会使用Python进行线性回归，还能对回归分析的理论基础有更深入的理解。