牛头刨床运动分析：解析法与Matlab实现

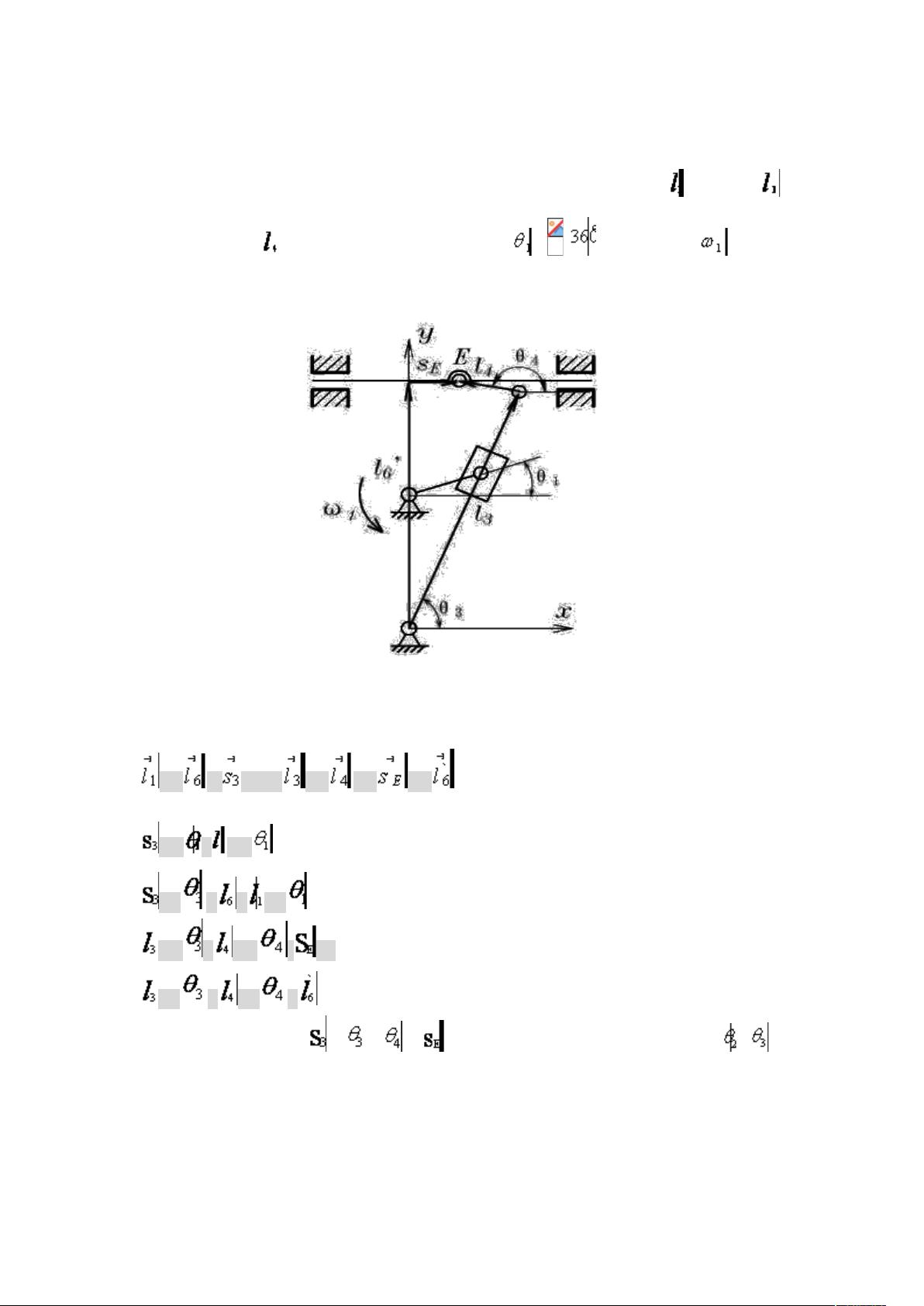
"本文主要介绍了如何使用解析法进行牛头刨床的运动分析，通过MATLAB编程实现。" 牛头刨床是一种常见的金属切削机床，它的运动分析涉及到机械工程中的动力学问题。解析法是解决这类问题的有效手段，通过数学公式和矩阵运算来确定各个部件的运动状态。 在牛头刨床的运动分析中，首先需要理解题意。给定了一些关键参数，如原动件1的方位角和等角速度，以及各个构件的尺寸。原动件1的方位角可以通过角度方程表示，等角速度为1 rad/s。目标是求解机构中各从动件的方位角、角速度和角加速度，以及E点（通常是刀具或工作台）的位移、速度和加速度的运动曲线。 为了解决这个问题，我们需要建立几何关系，利用封闭矢量方程。这里有两个封闭图形ABCA和CDEGC，它们可以帮助我们得到四个未知量的方程组。将这些方程转换为投影方程，可以解出[pic]、[pic]、[pic]和[pic]。接着，通过对时间的一次和二次导数，我们可以得到速度和加速度方程，这些通常会表示为矩阵形式。 MATLAB程序用于数值计算和图形化显示结果。程序中定义了相关的物理参数，如各个长度和角度，并且通过循环遍历时间范围来计算各个运动变量。在计算过程中，可能需要处理角度的正负和边界条件，例如当原动件1达到90度或270度时，某些角度可能需要特殊处理以避免计算上的不连续性。 MATLAB代码中，`clearall;clc;`用于清空当前工作空间和清除命令窗口。接下来，定义了各构件的长度和角度，然后通过循环计算每个时间步长的运动变量。在循环内部，计算了o3(m)和s3(m)等变量，这些都是基于之前建立的几何和运动方程。如果遇到特定角度，如90度和270度，需要特别处理o3(m)的值，以确保其正确性。 这个牛头刨床的运动分析实例展示了如何结合解析法和MATLAB编程来解决实际工程问题，这在机械设计、动力学建模和仿真等领域具有重要的应用价值。通过这样的分析，工程师可以更好地理解和优化机械设备的性能，确保其在运行过程中的稳定性和效率。