二叉树概念解析:从基本术语到满二叉树
版权申诉
31 浏览量
更新于2024-07-08
收藏 547KB PPTX 举报
"该资源是关于树和二叉树的第二讲,主要讲解二叉树的概念,适合课程学习参考。"
二叉树是计算机科学中数据结构的重要组成部分,尤其在算法设计和数据组织中占据着核心地位。在深入探讨二叉树之前,我们需要先回顾一下树的基本概念。
树是一种非线性数据结构,由n个节点组成,其中n可以是0,表示空树。当n大于0时,树有一个特殊的节点称为根节点,其余节点分为m个互不相交的子集,这些子集本身又是树,称为根节点的子树。这种层次关系使得树成为一种层次结构,便于表示具有层级关系的数据。
在树的基本术语中,节点的“度”是指该节点拥有的子节点数量。例如,节点A的度是3,因为它的子节点是B、C和D。树的度是指树中所有节点度数的最大值。根节点是没有父节点的节点,分支节点是有子节点的节点,而叶子节点是没有子节点的节点。路径长度是从一个节点到另一个节点经过的边的数量,路径上的边数减1等于路径上分支节点的数量。节点B的孩子是C、D、E,节点J的双亲是I,节点E和F是兄弟节点,D和F是堂兄弟节点,节点B的子孙包括E、F、G、H、I,而节点J的祖先包括A、B、C。
树的基本性质对于理解和操作树至关重要。性质1指出树中的节点数等于所有节点度数之和加1,这可以通过扩展公式1和2来表示。性质2说明在度为m的树中,第i层最多有mi-1个节点。性质3阐述了高度为h的m次树最多有2^h - 1个节点。
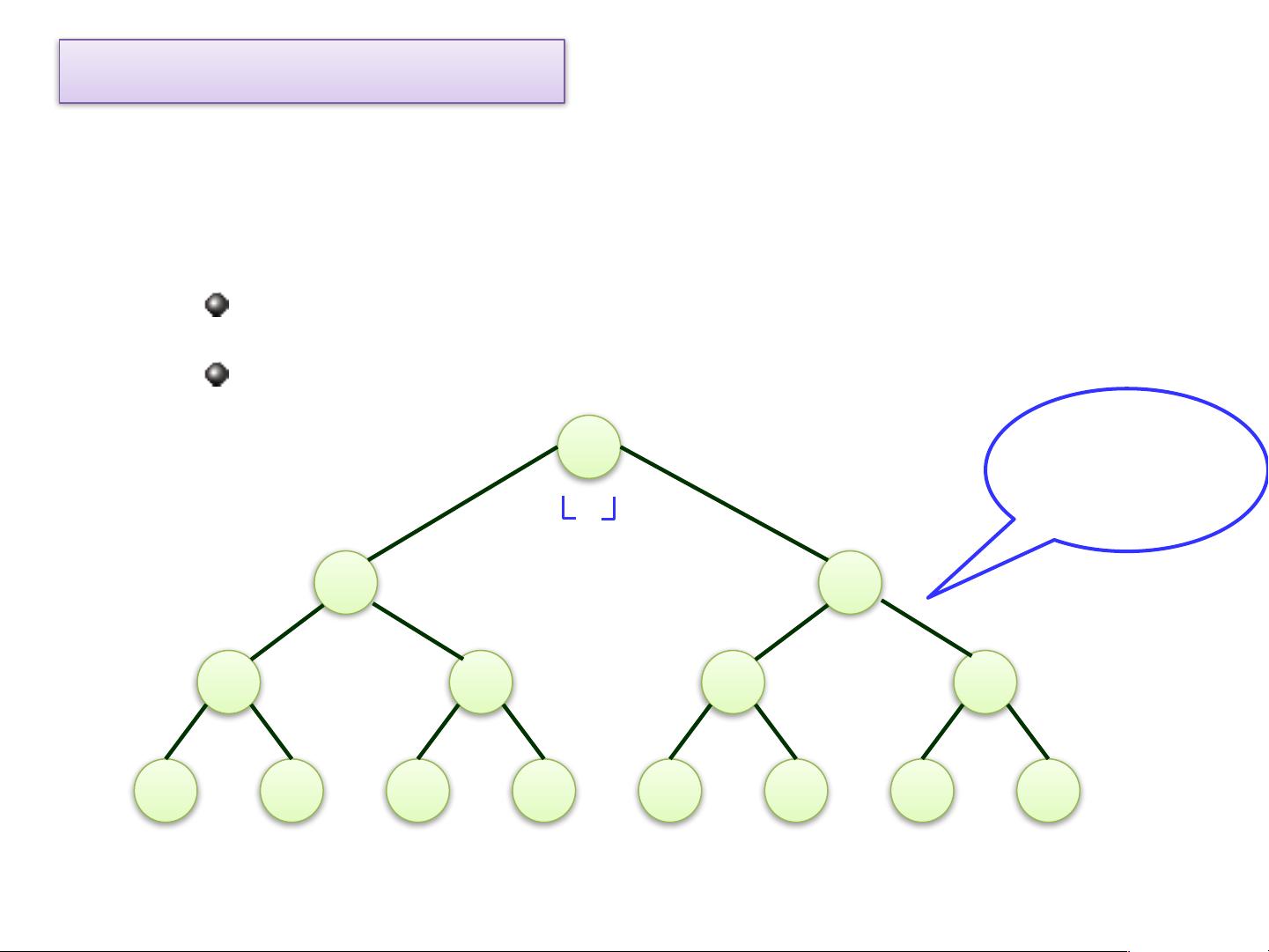
二叉树是树的一个特殊类型,每个节点最多有两个子节点,即左子树和右子树,且它们的顺序不能颠倒。二叉树有五种基本形态,从空二叉树到完全充满的二叉树。二叉树可以用多种方式表示,如树形表示、文氏图表示、凹入表示和括号表示。
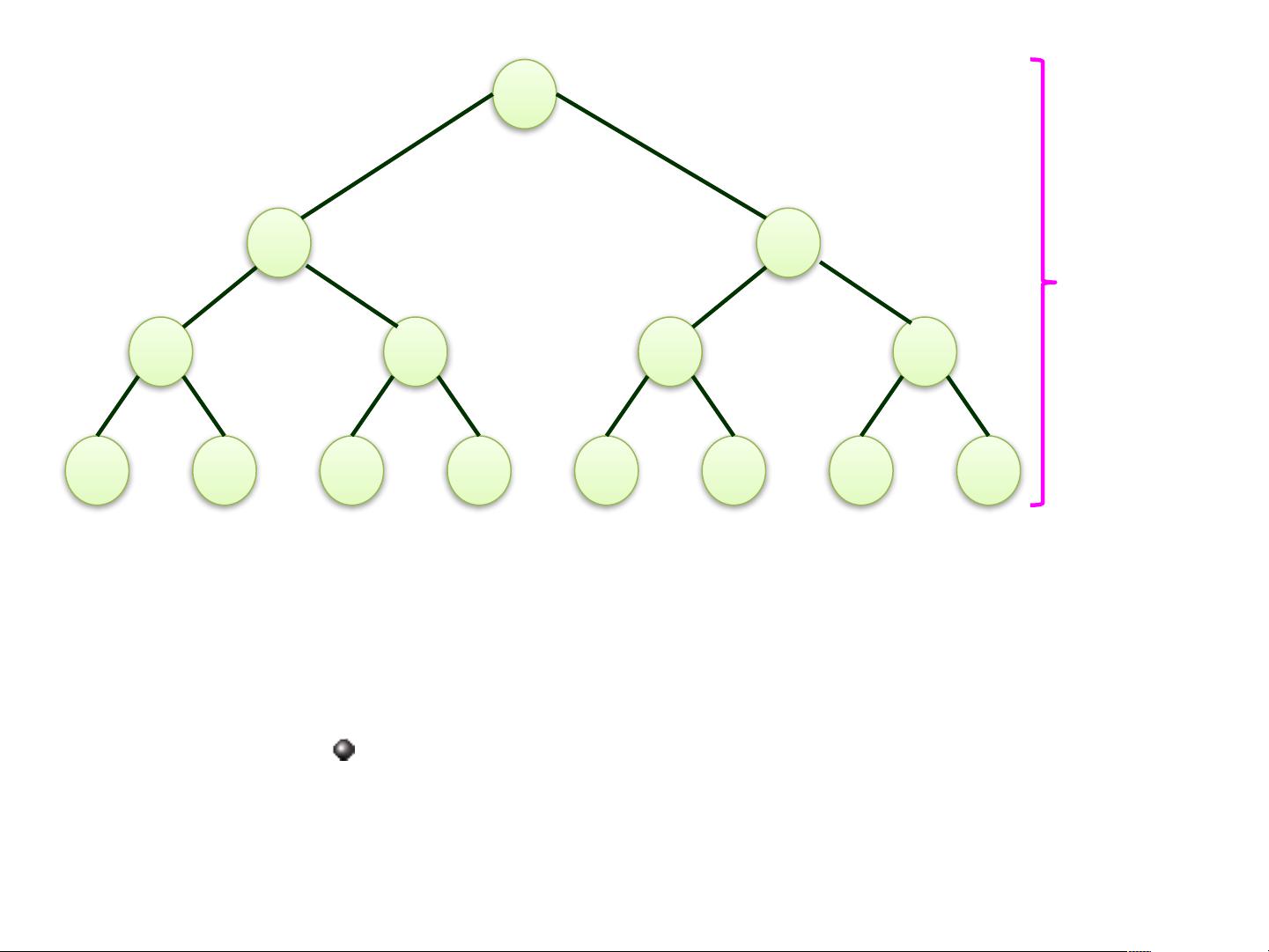
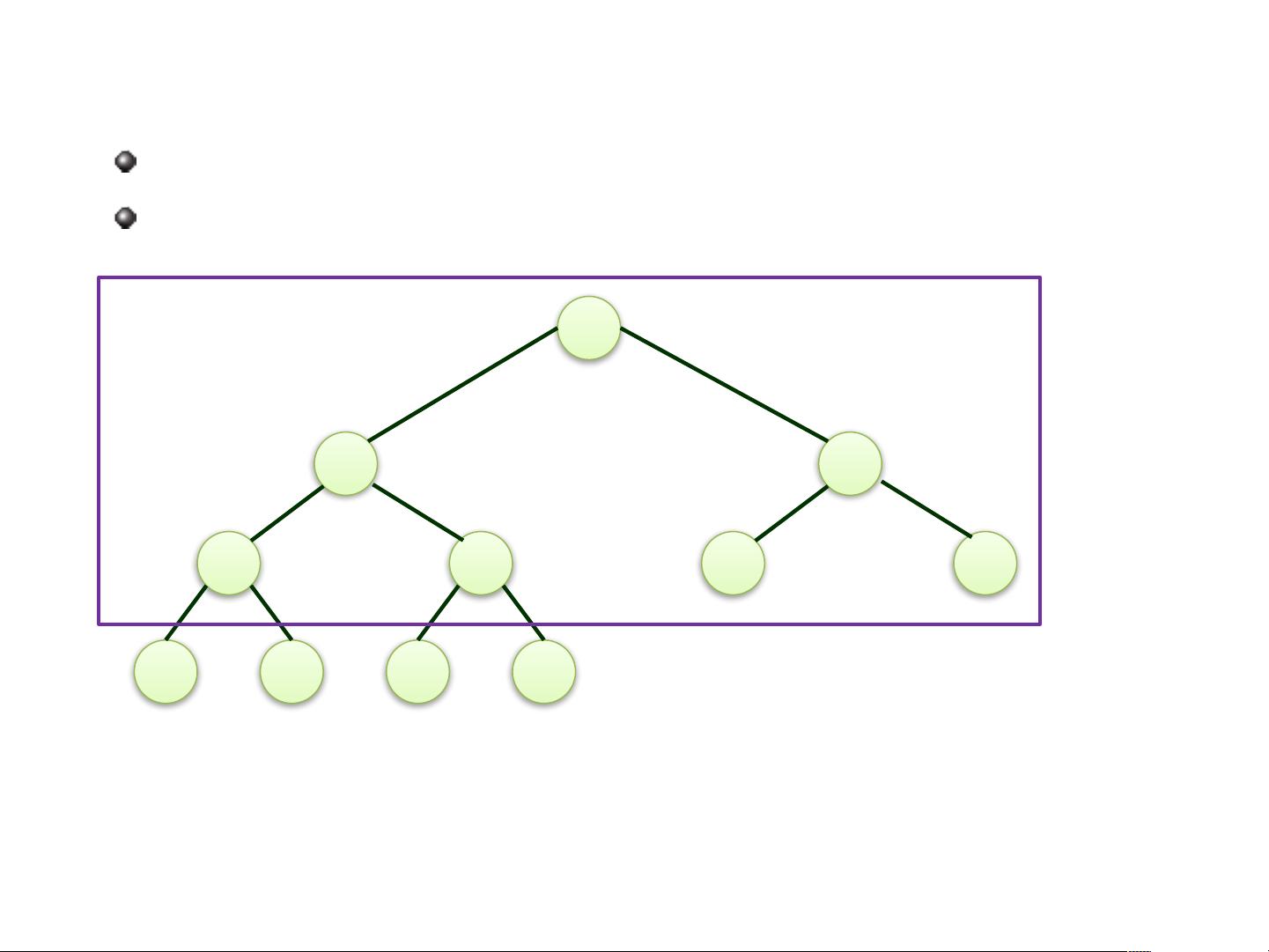
满二叉树是二叉树的一种特殊情况,其中每一层都有最多的节点,即第i层有2^(i-1)个节点。完全二叉树是另一种特殊的二叉树,除了最后一层可能不满之外,其他层都是满的,而且最后一层的所有节点都尽可能地靠左排列。
了解二叉树的特性对于理解和实现各种二叉树算法至关重要,如二叉搜索树、堆、哈夫曼树等。这些数据结构广泛应用于排序、查找、压缩和其他效率优化问题。因此,对二叉树的深入理解是计算机科学基础教育和专业发展的重要部分。
410 浏览量
185 浏览量
112 浏览量
190 浏览量
152 浏览量
107 浏览量
念广隶
- 粉丝: 5w+
- 资源: 6万+
最新资源
- 叉车变矩器故障诊断及处理.rar
- BULLDOG-开源
- 草图设备:一些草图格式的设备
- libdaisy-rust:菊花板的硬件抽象层实现
- clangular:lan角
- 行业文档-设计装置-一种拒油抗静电纸质包装材料.zip
- ICLR-Workshop-Challenge-1-CGIAR-Computer-Vision-for-Crop-Disease:Zindi竞赛的入门代码-ICLR Workshop Challenge#1
- aklabeth:Akalabeth aka'Ultima 0'的翻拍-开源
- snglpg:Занимаясь“在浏览器中设计”
- OpenCore-0.6.2-09-09.zip
- 摩尔斯电码,实现将字符转为摩尔斯电码的主体功能,能将摩尔斯电码通过串口上位机进行显示
- matlab布朗运动代码-Zombie:用于团队项目的MATLAB僵尸启示仿真(2016)
- 纯css3圆形发光按钮动画特效
- mvntest
- 版本:效用调查,专家和UX使用者,请指责一个集体经济团体,请参阅一份通俗的经济通函,一份从业者的各种困难和疑难解答,请参见网站实际内容
- OpenCore-0.6.1-09-08正式版.zip