定向传感器网络的概率覆盖模型与容错设计

66 浏览量更新于2024-08-28 收藏 2.4MB PDF 举报

"Probabilistic Coverage in Directional Sensor Networks" 是一篇发表于2017年8月4日的研究论文，由Pengju Si、Chengdong Wu、Yunzhou Zhang、Hao Chu和He Teng合作完成，收录在Springer Science+Business Media出版物中。本文主要关注的是在定向传感器网络（DSNs）中的概率感知模型设计，这对于环境监测的传感器网络性能至关重要。在传统上，环境因素和传感器本身的内在特性会显著影响定向传感器的感知能力，这使得简单的二元感知模型不再适用。因此，作者提出了对定向传感器网络进行更深入研究的必要性，旨在开发出更具实用性的概率感知模型。首先，他们参考了对全向传感器的普适概率感知模型，探讨了如何将这种模型应用于定向传感器的场景。论文的核心贡献之一是提出了一个基于指数衰减的概率感知模型。这个模型考虑了环境因素对传感器敏感度的影响，通过数学建模，能够更好地反映实际环境中定向传感器的响应可能性随距离的变化趋势。这意味着模型能够更准确地估计在不同方位和距离下，传感器成功检测目标的概率。接下来，为了提高系统的鲁棒性，作者进一步提出了一个故障容忍概率感知模型。他们考虑了两种主要类型的错误：定向误差（即传感器指向方向的不确定性）和旋转误差（传感器自身角度的偏离）。通过引入容错机制，即使在存在这些误差的情况下，模型也能保持一定程度的准确性，确保网络的正常运行。最后，结合指数衰减概率和故障容忍概率，论文构建了一个混合概率感知模型。这个模型综合了两者的优点，既能适应复杂多变的环境，又能处理传感器的非理想行为，从而提高了DSNs的整体覆盖率和可靠性。总结来说，"Probabilistic Coverage in Directional Sensor Networks"这篇论文着重于针对定向传感器网络的特殊性，提出了一套包含指数衰减概率、故障容忍性和混合策略的概率感知模型。这些模型的引入对于提升定向传感器网络在环境监测任务中的效能具有重要意义，对于研究者和工程师来说，提供了重要的理论支持和实践指导。"

intruders in different scenarios. In order to detect an

intruder, Onur et al. proposed the probabilistic detection

model with false alarm rate in [22].

Compared with traditional omni-directional sensors,

directional sensors provide much richer information of the

environment in the forms of images or sounds and hence

promise a huge potential in applications [2, 6]. Almost

existing works about DSNs considered the sensing model of

directional sensor as a sector, which is also the boolean

sensing model [10]. Yildiz et al. [28] investigated the problem

of determining optimal camera placement to achieve angular

coverage continuously over a given region. Some deployment

strategies for satisfying given coverage probability require-

ments with sectorial sensing models were designed in [19].

Most of existing works focused on considering the sensing

model for DSNs as a deterministic sensing model, ignoring

extraction the probabilistic factors. Then, more practical

factors for DSNs should be considered to better complete the

DSNs. Especially, Ahmed et al. [1] investigated the coverage

issues in wireless sensor networks based on probabilistic

sensing model and proposed a probabilistic coverage algo-

rithm to compute the coverage probability. The assumption is

valid for certain kind of sensors, which include the acoustic

sensor as a directional sensor. However, they only introduce

the sensor’s characteristics of signal propagation. Hence, in

this paper, we propose different sensing models for DSNs,

which consider more probabilistic factors.

3 Sensing models

In this section, the sensing models for DSNs are discussed.

Based on the deterministic sector sensing model, we ﬁrst

study two more realistic probabilistic sensing models,

which are called exponential decay probabilistic sensing

model and fault-tolerant probabilistic sensing model,

respectively. Then, a hybrid probabilistic sensing model for

DSNs is proposed by combining the above sensing models.

3.1 Deterministic sensing model

The commonly-used deterministic sector sensing model sim-

pliﬁes the coverage problem. Almost all the previous works

have been considered the sector sensing model for DSNs.

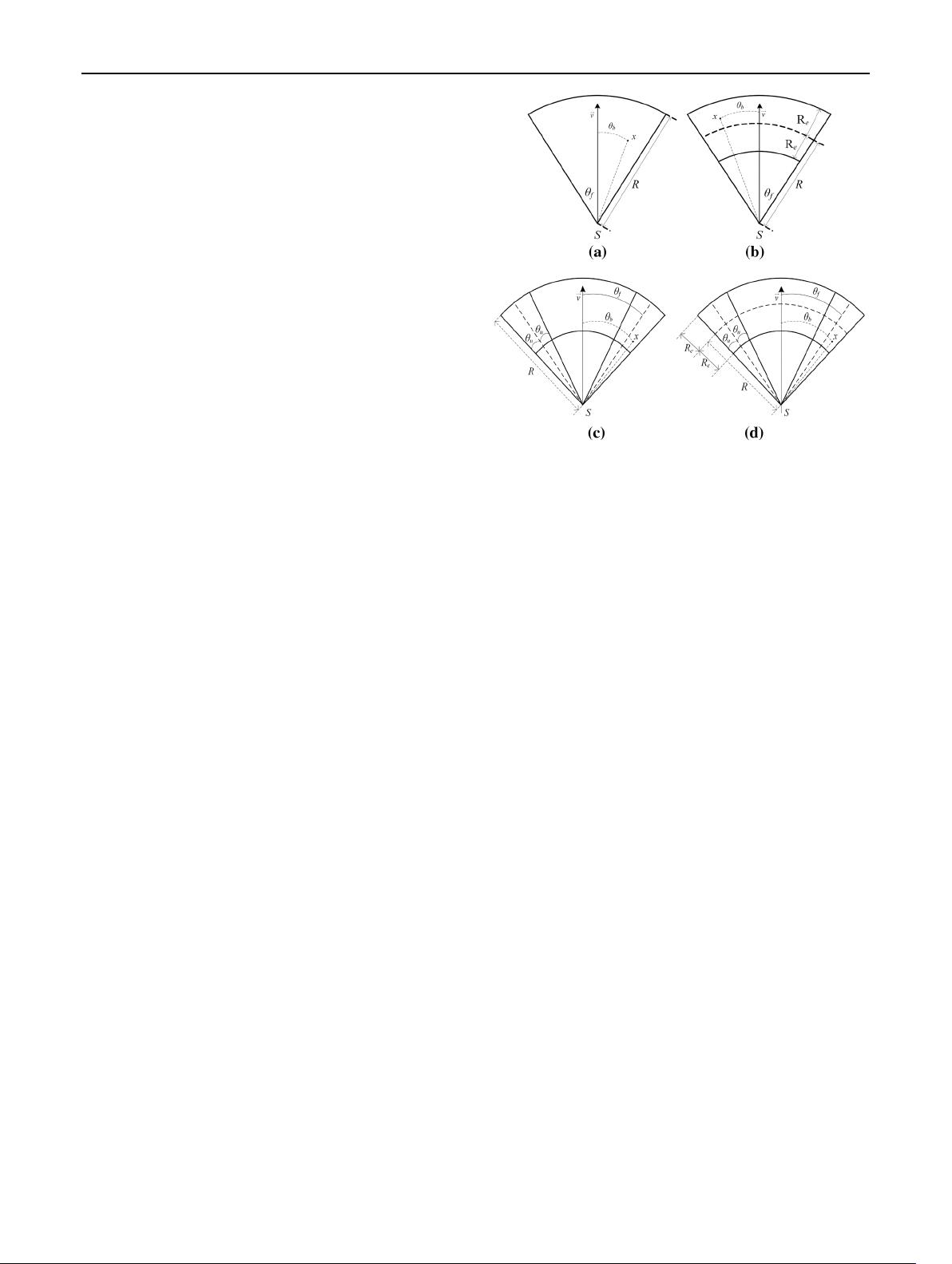
As depicted in Fig. 2(a), the deterministic sensing area

of directional sensor is sector-shaped region, which can be

denoted by 4-tuple ðS; R; h

; v

Þ. S is the location coordi-

nate in a two-dimension plane, and it also denotes the

directional sensor. R points out the maximum sensing

radius. h

indicates sensing offset angle which equals to the

half of the vertex angle of sector. Note that the omni-

directional sensing model is a special case of the deter-

ministic directional sensing model when h

¼ p. v

is a

unit vector, and denotes the viewing angle, which repre-

sents the orientation of a directional sensor.

It can be determined whether a point x is covered by the

directional sensor S or not by the following:

R ð1Þ

 v

 Sx



 cos h

ð2Þ

In other words, the deterministic sensing model for DSNs

can be described by:

pðxÞ¼

0; ðd [ RÞ_ h

[ h



;

1; ðd RÞ^ h

h





ð3Þ

where d and h

are the euclidean distance between x and

S and the offset angle between Sx

and orientation of

directional sensor, respectively.

3.2 Exponential decay probabilistic sensing model

Probabilistic sensing models assume that the sensing prob-

ability is a decreasing function of the sensing distance.

Actually, Sensors typically perform the sensing task proba-

bilistic—for two main reasons: (i) The signal propagation

from a target to a sensor follows a probabilistic model [1].

The probability of detection of a target by a sensor decreases

exponentially with increase in distance between the target

and sensor. (ii) Especially for underwater acoustic sensors,

the signal roughly decays based on the path loss log normal

shadowing model by blocking effect of water.

As shown in Fig. 2(b), the exponential decay proba-

bilistic sensing model for DSNs can be deﬁned by 5-tuple

Fig. 2 Sensing models for DSNs: a deterministic sensing model;

b exponential decay probabilistic sensing model; c fault-tolerant

probabilistic sensing model; d hybrid probabilistic sensing model

Wireless Netw (2019) 25:355–365 357

123

剩余10页未读，继续阅读

weixin_38607026

粉丝: 9
资源: 914

定向传感器网络的概率覆盖模型与容错设计

Probabilistic reasoning in intelligent systems: networks of plausible inference

Probabilistic Reasoning in Multiagent Systems: A Graphical Models Approach

A Game-Theoretic Approach to Stimulate Cooperation for Probabilistic Routing in Opportunistic Networks

Probabilistic Sensor Models

Probabilistic methods in algorithmic discrete mathematics

Probabilistic Reasoning in Multi-Agent Systems

Bayesian Modeling and Probabilistic Programming in Python.zip

Disrupted topological organization of structural networks revealed by probabilistic diffusion tractography in Tourette syndrome children

Robust control invariance of probabilistic Boolean control networks

Probabilistic Networks — An Introduction to Bayesian Networks and Influence Diagrams

最新资源