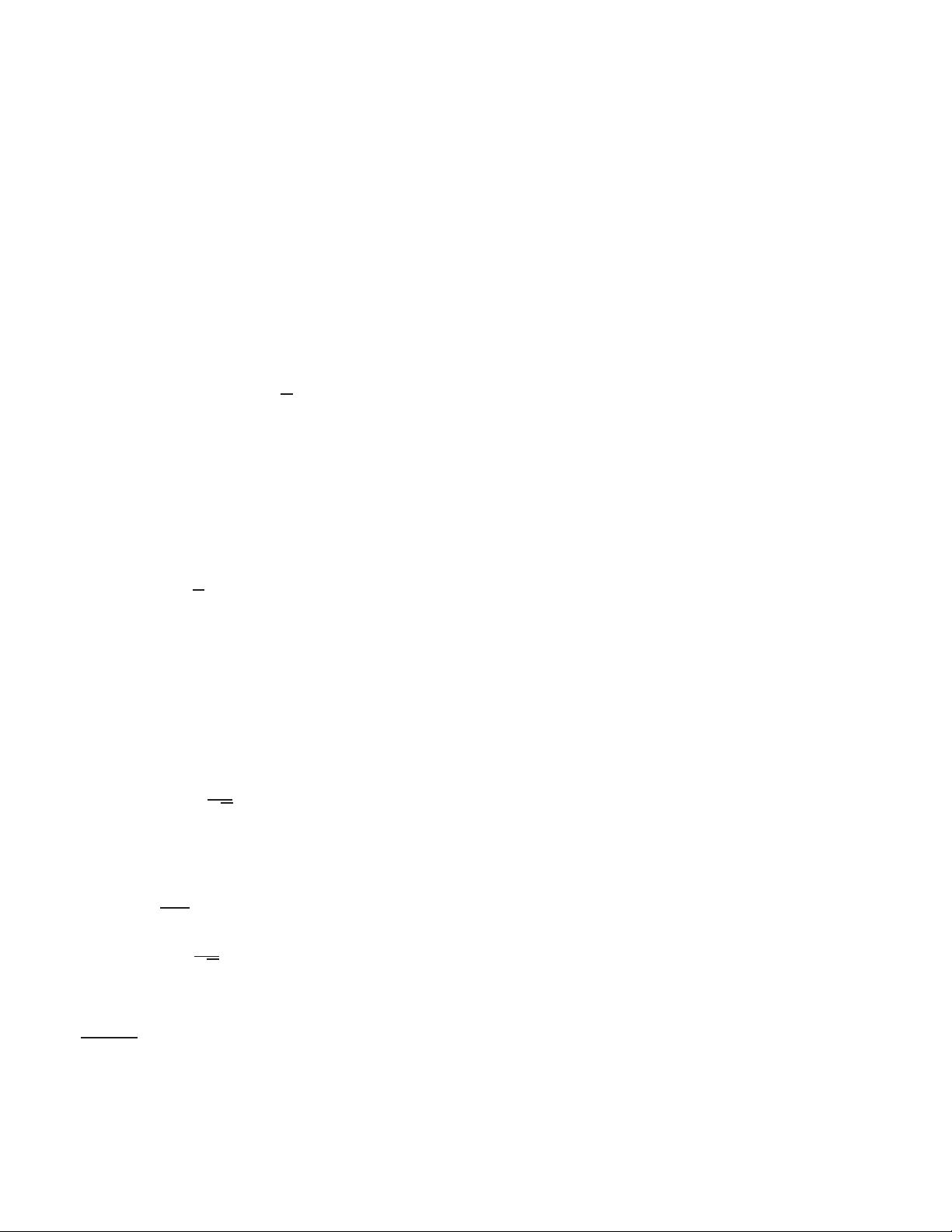量子算法：超越经典计算的代数问题解决方案

需积分: 9 127 浏览量更新于2024-07-17 1 收藏 888KB PDF 举报

量子算法对于代数问题的研究是当前理论计算机科学中的一个核心领域，它揭示了量子计算在某些任务上的巨大优势，尤其是在处理传统计算机难以解决的问题时。本文标题《Quantum algorithms for algebraic problems》由Andrew M. Childs和Wim van Dam共同撰写，着重探讨了那些能在经典计算基础上实现超多项式加速的量子算法，特别是那些具有代数性质的问题。首先，文章开篇强调了量子计算机能够执行超越传统计算机效率的算法，最具代表性的是Peter Shor于2001年提出的量子因数分解算法（Quantum Factoring Algorithm），该算法能在多项式时间内解决因数分解问题，而这是已知的经典算法面临重大困难的问题。这一成就不仅证明了量子计算在特定问题上的优越性，而且推动了构建大规模量子计算机的艰巨任务。量子算法的优势在于其能够利用量子比特的叠加态和纠缠性质，这些特性使得量子计算机在解决某些问题时能够以指数级的速度提升效率。这类问题往往与线性代数、群论、数论等数学分支密切相关，因此具有明显的代数味道。例如，Grover's search algorithm（格罗弗搜索算法）可以显著加快搜索数据库或在无结构列表中查找元素的速度，而HHL算法（ Harrow-Hassidim-Lloyd）则提供了在量子系统中进行高效线性方程求解的方法。本文深入剖析了量子算法在代数问题上的应用，如量子线性系统算法（QLSA），它能够解决线性系统的近似求解问题，这对于机器学习和优化问题有潜在的应用。此外，量子编码理论中的各种错误纠正码（如量子重复码和量子低密度 parity check码）也依赖于量子算法的高效性，它们在保护量子信息免受噪声影响方面起着关键作用。在实际应用中，研究人员致力于寻找更多具有超多项式速度提升的量子算法，这包括在数论、组合优化、密码学（如量子密钥分发）以及物理学中的模型模拟等方面。理解这些算法背后的原理，以及如何将它们转化为实际可行的量子电路设计，是量子计算机科学中的前沿挑战。这篇论文为读者提供了一个全面的视角，探讨了量子算法如何通过代数手段解决经典计算难题，并展示了量子计算在当今信息技术领域的潜在影响。随着量子技术的发展，这些代数问题的量子解决方案有望引领未来计算模式的革新。

4. Apply the Fourier transform over Z/NZ, giving

∑

y∈Z/NZ

−1

∑

j=0

(s+ jr)y

|yi. (32)

By the identity

M−1

∑

j=0

= M δ

j,y mod M

(33)

(applied with M = N/r, so ω

jry

= ω

), only the values

y ∈{0, N/r,2N/r, ...,(r−1)N/r} experience construc-

tive interference, and Eq. (

32) equals

√

r−1

∑

k=0

|kN/ri. (34)

5. Measure this state in the computational basis, giving

some integer multiple kN/r of N/r. Dividing this inte-

ger by N gives the fraction k/r, which, when reduced to

lowest terms, has r/ gcd(r,k) as its denominator.

6. Repeating the above gives a second denominator

r/ gcd(r,k

′

). If k and k

′

are relatively prime, the

least common multiple of r/ gcd(r,k) and r/ gcd(r, k

′

)

is r. The probability of this happening is at least

∏

p prime

(1−

) = 6/π

≈ 0.61, so the algorithm suc-

ceeds with constant probability.

B. Computing discrete logarithms

Let C = hgi be a cyclic group generated by an element g,

with the group operation written multiplicatively. Given an

element x ∈C, the discrete logarithm of x in C with respect to

g, denoted log

x, is the smallest non-negative integer ℓ such

that g

ℓ

= x. The discrete logarithm problem is the problem

of calculating log

x given g and x. (Notice that for additive

groups such as G = Z/pZ, the discrete log represents division:

log

x = x/g mod p.)

1. Discrete logarithms and cryptography

Classically, the discrete logarithm seems like a good candi-

date for a one-way function. We can efﬁciently compute g

ℓ

even if ℓ is exponentially large (in log|C|), by repeated squar-

ing. But given x, it is not immediately clear how to compute

log

x without checking exponentially many possibilities.

The apparent hardness of the discrete logarithm problem

is the basis of the Difﬁe-Hellman key exchange protocol

(

Difﬁe and Hellman, 1976), the earliest published public-key

cryptographic protocol. The goal of key exchange is for two

distant parties, Alice and Bob, to agree on a secret key using

only an insecure public channel. The Difﬁe-Hellman protocol

works as follows:

1. Alice and Bob publicly agree on a large prime p and

an integer g of high order. For simplicity, suppose they

choose a g for which hgi = (Z/pZ)

(i.e., a primitive

root modulo p). (In general, ﬁnding such a g might be

hard, but it can be done efﬁciently given certain restric-

tions on p.)

2a. Alice chooses some a ∈ Z/(p −1)Z uniformly at ran-

dom. She computes A := g

mod p and sends the result

to Bob (keeping a secret).

2b. Bob chooses some b ∈ Z/(p −1)Z uniformly at ran-

dom. He computes B := g

mod p and sends the result

to Alice (keeping b secret).

3a. Alice computes K := B

= g

mod p.

3b. Bob computes K = A

= g

mod p.

At the end of the protocol, Alice and Bob share a key K, and

an eavesdropper Eve has only seen p, g, A, and B.

The security of the Difﬁe-Hellman protocol relies on the

assumption that discrete log is hard. Clearly, if Eve can

compute discrete logarithms, she can recover a and b, and

hence the key. But it is widely believed that the discrete

logarithm problem is difﬁcult for classical computers. The

best known algorithms for general groups, such as Pollard’s

rho algorithm and the baby-step giant-step algorithm, run in

time O(

|C|). For particular groups, it may be possible

to do better: for example, over (Z/pZ)

with p prime, the

number ﬁeld sieve is conjectured to compute discrete loga-

rithms in time 2

O((log p)

1/3

(loglog p)

2/3

)

(

Gordon, 1993) (whereas

the best known rigorously analyzed algorithms run in time

√

log ploglog p)

(Pomerance, 1987)); but this is still super-

polynomial in log p. It is suspected that breaking the Difﬁe-

Hellman protocol is essentially as hard as computing the dis-

crete logarithm.

This protocol by itself only provides a means of exchanging

a secret key, not of sending private messages. However, Alice

and Bob can subsequently use their shared key in a symmetric

encryption protocol to communicate securely. The ideas be-

hind the Difﬁe-Hellman protocol can also be used to directly

create public-key cryptosystems (similar in spirit to the widely

used RSA cryptosystem), such as the ElGamal protocol; see

for example (

Buchmann, 2004; Menezes et al., 1996).

2. Shor’s algorithm for discrete log

Although the problem appears to be difﬁcult for classical

computers, quantum computers can calculate discrete loga-

rithms efﬁciently. Recall that we are given some element x of

a cyclic group C = hgi and we would like to calculate log

the smallest non-negative integer ℓ such that g

ℓ

= x.

It is nevertheless an open question whether, given the ability to break the

protocol, Eve can calculate discrete logarithms. Some partial results on this

question are known (

den Boer, 1990; Maurer and Wolf, 1999).

For simplicity, assume that the order of the group, N := |C|,

is known. For example, if C = (Z/pZ)

, then we know

N = p −1. If we do not know N, we can determine it ef-

ﬁciently using Shor’s algorithm for period ﬁnding over Z,

which we discuss in Section

IV.D. We also assume that x 6= g

(i.e., log

x 6= 1), since it is easy to check this.

The algorithm of

Shor (1997) for computing discrete loga-

rithms works as follows:

Algorithm 3 (Discrete logarithm).

Input: A cyclic group C = hgi and an element x ∈C.

Problem: Calculate log

1. If necessary, using the period ﬁnding algorithm of Sec-

tion

IV.D, determine the order N = |C|.

2. Create the uniform superposition

|Z/NZ ×Z/NZi=

∑

α,β∈Z/NZ

|α,βi (35)

over all elements of the additive Abelian group Z/NZ×

Z/NZ.

3. Deﬁne a function f : Z/NZ ×Z/NZ →C as follows:

f(α,β) = x

. (36)

Compute this function in an ancilla register, giving

∑

α,β∈Z/NZ

|α,β, f (α,β)i. (37)

4. Discard the ancilla register.

Since f (α,β) = g

αlog

x+β

f is constant on the lines

:= {(α,β) ∈ (Z/NZ)

: αlog

x+ β = γ}, (38)

so the remaining state is a uniform superposition over

group elements consistent with a uniformly random, un-

known γ ∈ Z/NZ, namely

i =

√

∑

α∈Z/NZ

|α,γ−αlog

xi. (39)

5. Now we can exploit the symmetry of the quantum state

by performing a QFT over Z/NZ ×Z/NZ, giving

3/2

∑

α,µ,ν∈Z/NZ

µα+ν(γ−αlog

|µ,νi (40)

√

∑

ν∈Z/NZ

νγ

|νlog

x,νi (41)

where we used the identity Eq. (

33).

Note that if we were to measure the ancilla register instead of discarding

it, the outcome would be unhelpful: each possible value g

occurs with

equal probability, and we cannot obtain γ from g

unless we know how to

compute discrete logarithms.

6. Measure this state in the computational basis. We

obtain some pair (νlog

x,ν) for a uniformly random

ν ∈Z/NZ.

7. Repeating the above gives a second pair (ν

′

log

x,ν

′

)

with a uniformly random ν

′

∈ Z/NZ, independent of ν.

With constant probability (at least 6/π

≈ 0.61), ν and

′

are coprime, in which case we can ﬁnd integers λ

and λ

′

such that λν+ λ

′

= 1. Thus we can determine

λνlog

x+ λ

′

log

x = log

This algorithm can be carried out for any cyclic group C,

given a unique representation of its elements and the ability to

efﬁciently compute products and inverses in C. To efﬁciently

compute f(α,β), we must compute high powers of a group

element, which can be done quickly by repeated squaring.

In particular, Shor’s algorithm for discrete log breaks the

Difﬁe-Hellman key exchange protocol described above, in

whichC = (Z/pZ)

. In Section

IV.F we discuss further appli-

cations to cryptography, in which C is the group correspond-

ing to an elliptic curve.

C. Hidden subgroup problem for ﬁnite Abelian groups

Algorithms

2 and 3 solve particular instances of a more

general problem, the Abelian hidden subgroup problem (or

Abelian HSP). We now describe this problem and show how

it can be solved efﬁciently on a quantum computer.

Let G be a ﬁnite Abelian group with group operations writ-

ten additively, and consider a function f : G → S, where S is

some ﬁnite set. We say that f hides the subgroup H ≤ G if

f(x) = f (y) if and only if x−y ∈ H (42)

for all x,y ∈ G. In the Abelian hidden subgroup problem, we

are asked to ﬁnd a generating set for H given the ability to

query the function f.

It is clear that H can in principle be reconstructed from the

entire truth table of f. Notice in particular that f(0) = f(x)

if and only if x ∈ H: the hiding function is constant on the

hidden subgroup, and does not take that value anywhere else.

Furthermore, ﬁxing any y ∈ G, we see that f(y) = f(x) if and

only if x ∈ y + H := {y + h : h ∈ H}, a coset of H in G with

coset representative y. So f is constant on the cosets of H in

G, and distinct on different cosets.

The simplest example of the Abelian hidden subgroup

problem is Simon’s problem, in which G = (Z/2Z)

and

H = {0,x} for some unknown x ∈ (Z/2Z)

. Simon’s efﬁ-

cient quantum algorithm for this problem (

Simon, 1997) led

the way to Shor’s algorithms for other instances of the Abelian

HSP.

The period ﬁnding problem discussed in Section

IV.A is the

Abelian HSP with G = Z/NZ. The subgroups of G are of the

form H = {0, r,2r,. . .,N −r} (of order |H|= N/r), where r is

a divisor of N. Thus a function hides H according to Eq. (

42)

precisely when it is r-periodic, as in Eq. (

28). We have already

seen that such a subgroup can be found efﬁciently.

The quantum algorithm for discrete log, as discussed in

Section

IV.B

, solves an Abelian hidden subgroup problem in

the group Z/NZ ×Z/NZ. The function deﬁned in Eq. (

36)

hides the subgroup

H = {(α,αlog

x) : α ∈ Z/NZ}. (43)

Shor’s algorithm computes log

x by ﬁnding this hidden sub-

group.

More generally, there is an efﬁcient quantum algorithm to

identify any hidden subgroup H ≤G of a known ﬁnite Abelian

group G. (In Section VII.C we relax the commutativity re-

striction to the requirement that H is a normal subgroup of G,

which is always the case if G is Abelian.) The algorithm for

the general Abelian hidden subgroup problem is as follows:

Algorithm 4 (Abelian hidden subgroup problem).

Input: A black-box function f : G →S hiding some H ≤ G.

Problem: Find a generating set for H.

1. Create a uniform superposition |Gi over the elements

of the group.

2. Query the function f in an ancilla register, giving the

state

|G|

∑

x∈G

|x, f(x)i. (44)

3. Discard the ancilla register, giving the coset state

|s+ Hi=

|H|

∑

y∈H

|s+ yi (45)

for some unknown, uniformly random s ∈ G. Equiva-

lently, the state can be described by the density matrix

|G|

∑

s∈G

|s+ Hihs+ H|. (46)

4. Apply the QFT over G to this state. According to the

deﬁnition of the QFT in Eq. (

9), the result is

|H|·|G|

∑

ψ∈

∑

y∈H

ψ(s+ y)|ψi (47)

|H|

|G|

∑

ψ∈

ψ(s)ψ(H)|ψi (48)

where

ψ(H) :=

|H|

∑

y∈H

ψ(y). (49)

If ψ(y) = 1 for all y ∈ H, then clearly ψ(H) = 1. On

the other hand, if there is any y ∈H with ψ(y) 6= 1 (i.e.,

if the restriction of ψ to H is not the trivial character

of H), then by the orthogonality of distinct irreducible

characters (Theorem

6 in Appendix B), ψ(H) = 0. Thus

we have the state

[

s+ Hi :=

|H|

|G|

∑

ψ∈

G,Res

ψ=1

ψ(s)|ψi (50)

or, equivalently, the mixed quantum state

|H|

|G|

∑

ψ∈

G,Res

ψ=1

|ψihψ|, (51)

where Res

ψ = 1 means that ψ(h) = 1 for all h ∈H.

5. Measure in the computational basis. Then we obtain

one of the |G|/|H| characters ψ ∈

G that is trivial

on the hidden subgroup H, with every such charac-

ter occurring with equal probability |H|/|G|. Letting

kerψ := {g ∈ G : ψ(g) = 1} denote the kernel of the

character ψ (which is a subgroup of G), we learn that

H ≤ kerψ.

6. Repeat the entire process T times, obtaining characters

,. . . , ψ

, and output a generating set for K

, where

j=1

kerψ

. We are guaranteed that H ≤ K

for

any t. A simple calculation shows that if K

6= H, then

t+1

|/|K

| ≤ 1/2 with probability at least 1/2. Thus,

we can choose T = O(log|G|) such that K

= H with

high probability.

In summary, given a black-box function f hiding a sub-

group H of a known ﬁnite Abelian group G, a quantum com-

puter can determine H in time poly(log|G|), and in particular,

using only poly(log|G|) queries to the function f . Of course,

this assumes that we can efﬁciently implement group opera-

tions in G using some unique representation of its elements.

In contrast, the Abelian hidden subgroup problem is typi-

cally hard for classical computers. For example, an argument

based on the birthday problem shows that even the simple

case of Simon’s problem (where G = (Z/2Z)

) has classical

query complexity Ω(

√

) (Simon, 1997). While certain spe-

cial cases are easy—for example, since the only subgroups

of Z/pZ with p prime are itself and the trivial subgroup, pe-

riod ﬁnding over Z/pZ is trivial—the classical query com-

plexity of the Abelian HSP is usually exponential. In partic-

ular, one can show that if G has a set of N subgroups with

trivial pairwise intersection, then the classical query complex-

ity of the HSP in G is Ω(

√

N). (For a proof in the case where

G = F

×F

, see

de Beaudrap et al. (2002).)

D. Period ﬁnding over Z

In the previous section, we saw that the Abelian HSP can

be solved efﬁciently over any known ﬁnite Abelian group.

In this section we consider the HSP over an inﬁnite Abelian

group, namely Z (Shor, 1997). Similar ideas can be used

to solve the HSP over any ﬁnitely generated Abelian group

(

Mosca and Ekert, 1999). (For an Abelian group that is not

ﬁnitely generated, new ideas are required, as we discuss in

Section V.D.)

The HSP in Z is of interest when we are faced with a pe-

riodic function f over an unknown domain. For example,

Shor’s factoring algorithm (Section IV.E) works by ﬁnding the

period of a function deﬁned over Z. Without knowing the fac-

torization, it is unclear how to choose a ﬁnite domain whose

剩余51页未读，继续阅读

Dai&Wenjing

粉丝: 0
资源: 5

量子算法：超越经典计算的代数问题解决方案

Quantum Algorithms for Optimization and Polynomial Systems

Practical Quantum Computing for Developers

Quantum Algorithms via Linear Algebra

Explain quantum computing in simple terms

unity+quantum软件讲义

modern quantum mechanics and solutions for the exercices

quantum espresso geometry optimization

quantum espresso windows

最新资源