7
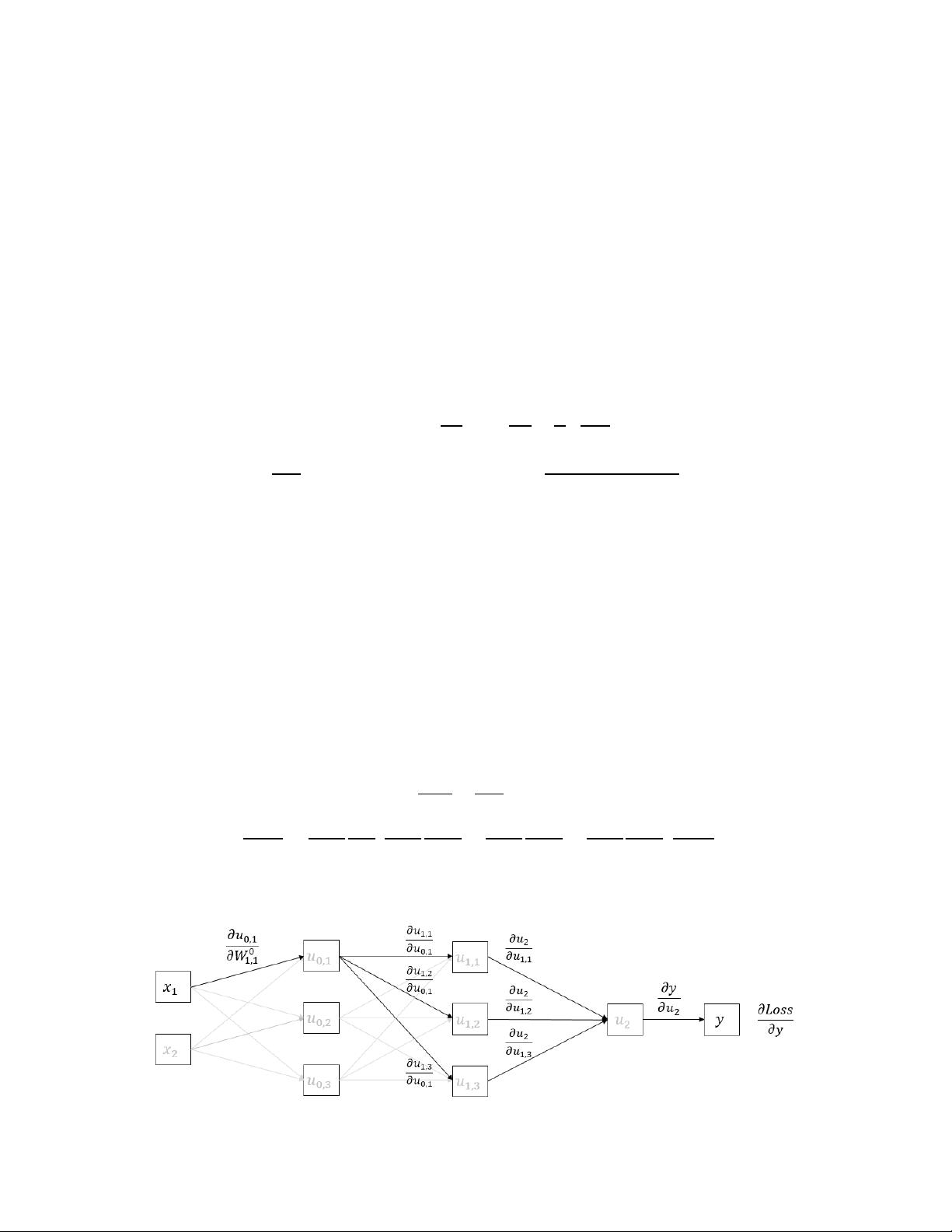
Figure 3: The derivative for a first layer parameter
,
with respect to the loss calculated by chaining
derivatives across all network branches.
SGD on deep neural networks typically uses a minibatch instead of a single observation to approximate
the derivative at each iteration. The learning rate , which represents how fast the parameter descends to its
cost minimizing value, may also need gradual updates itself. “A learning rate that is too small leads to painfully
slow convergence, while a learning rate that is too large can hinder convergence and cause the loss function to
fluctuate around the minimum or even to diverge” [68]. This relates to three problems with the standard SGD
update rule, namely, (1) the learning rate is not adjusted at different learning stages, (2) the same learning rate
applies to all parameters and (3) the learning rate does not depend on the local cost function surface (just the
derivative). Newton et al. [61] provide an overview of stochastic gradient descent improvements for
optimization. As an example, Byrd et al. [10] adjust sample size in every iteration to a minimum value such that
the standard error of the estimated gradient is small relative to its norm. Iterate-averaging methods allow long
steps within the basic SGD iteration but average the resulting iterates offline, to account for the increased noise
in the iterates.
A few variants of gradient descent have been found to be particularly efficient for deep neural networks.
Momentum SGD [65], one of the most common variants, accumulates gradients over a few update iterations.
Nesterov’s accelerated gradient [60], Adagrad [73], Adadelta [88] and RMSProp are a few other improvements
that work well on a case-by-case basis. The Adam optimizer [38], likely the most widely used in deeper
architectures, is an improvement on RMSProp. It accumulates the average of both the gradients
L
and their
second order moments
(
L
)
, then performs updates in proportion to these two quantities
/
.
=
+
(
1
)
L
;
=
+
(
1
)
(
L
)
;
2.2 Optimization Challenges
The SGD optimization faces two crucial challenges, namely, underfitting and overfitting. First, the gradient
of the loss with respect to layer parameters is small for early layers [77]. This is the result of nonlinear activations
(e.g., sigmoid, tanh) that repeatedly map their input onto a small range between [0,1]. Thus, the eventual output
loss value is relatively insensitive to early layer parameters. A very small gradient means that the parameter
values descend towards the cost minimizing optimal slowly. This is called the vanishing gradient problem. In
practice, a very slow optimization means that parameters are suboptimal (and underfit) even after an extremely
Electronic copy available at: https://ssrn.com/abstract=3395476