计算机实现维纳滤波器去除噪声的分析与应用

"该文档是关于维纳滤波器的计算机实现，主要涉及信号处理和噪声去除技术。" 维纳滤波器是一种在信号处理领域中广泛应用的线性滤波方法，尤其适用于从噪声中恢复信号。在计算机实现中，它能够通过优化算法来最小化输出信号与期望信号之间的均方误差，从而达到最佳的滤波效果。在本实验中，维纳滤波器被用于处理加性噪声信号，即信号x(n)是由有用信号s(n)和噪声v(n)组成。 实验的主要目标包括： 1. 使用编程方法实现加性噪声信号的维纳滤波。 2. 比较计算机模拟实验结果与理论分析结果，探究影响滤波效果的因素。 3. 应用维纳滤波一步纯预测方法估计信号生成模型的参数。 实验原理基于维纳-霍夫方程，该方程提供了解决线性滤波问题的数学基础。在给定输入信号x(n)和其与期望信号s(n)的相关函数φxx和φxs的情况下，可以通过求解逆相关矩阵来得到滤波器系数h(n)。对于实际应用，通常使用最佳FIR（有限 impulse response）维纳滤波器，其公式为h = R^-1xx * rxs，其中Rxx是输入信号的自相关矩阵，rxs是输入信号与期望信号的互相关矩阵。 实验中，信号s(n)由线性递归模型定义，即s(n) = a*s(n-1) + w(n)，其中a是递归系数，w(n)是高斯白噪声。噪声v(n)也被设定为高斯白噪声，且与s(n)不相关。为了理解维纳滤波的原理，尽管在实际情况下s(n)通常是未知的，但在实验中s(n)是已知的。 实验步骤包括： 1. 设计程序流程图。 2. 编写并运行程序，其中L=5000，N=10。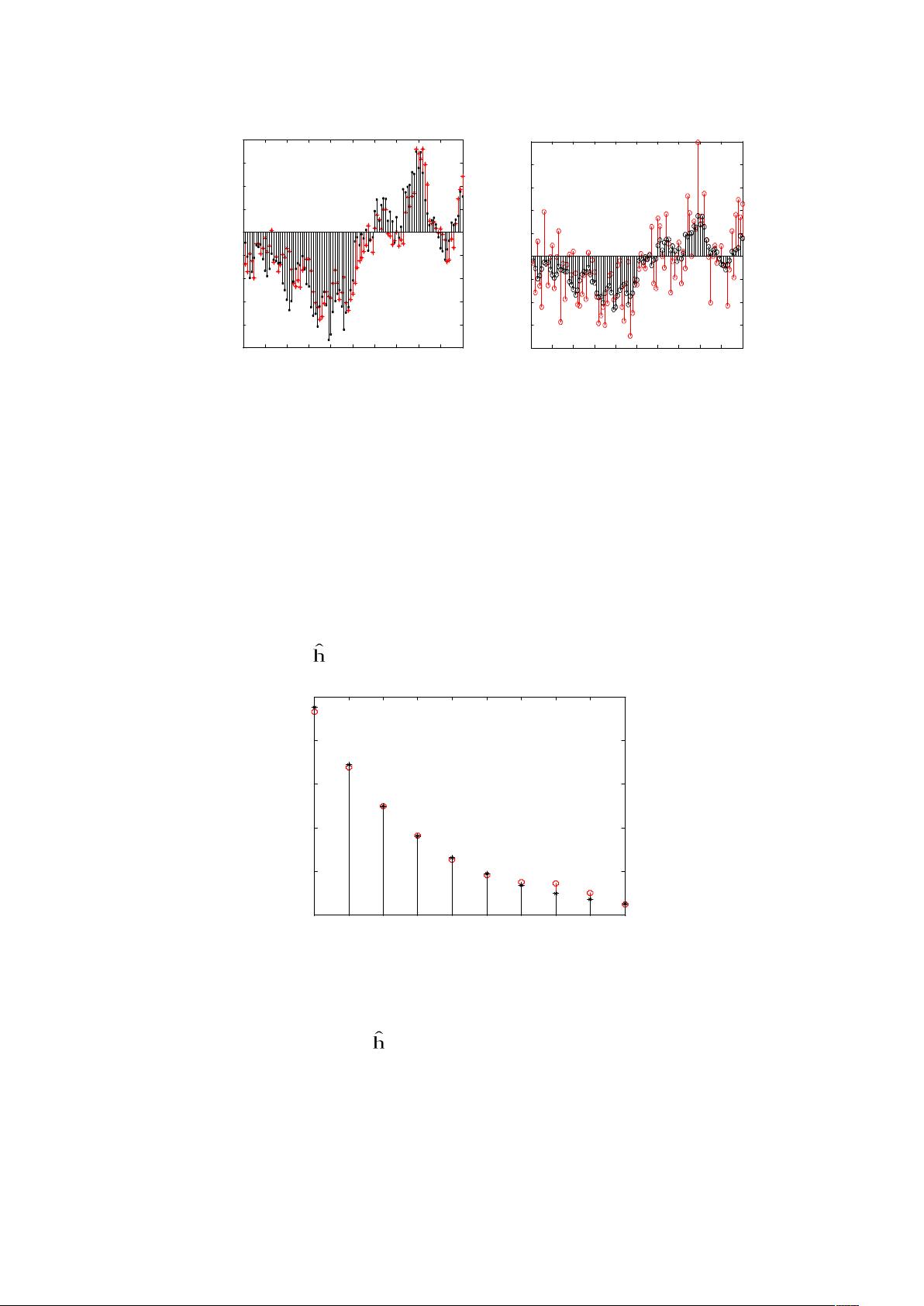 3. 分析结果，比较维纳滤波前后信号的变化以及滤波器系数的估计。 实验结果表明，经过维纳滤波后，信号x(n)更接近于原始的s(n)，证明了滤波的有效性。同时，通过与理想的h(n)进行比较，可以评估滤波器的性能。 维纳滤波器的计算机实现是一个理解和验证滤波理论的重要实践，它帮助我们深入理解如何从噪声中提取有用信号，并且通过调整滤波器参数，可以优化滤波效果，适应不同的噪声环境和信号特性。在实际的信号处理任务中，例如图像处理、音频去噪等，维纳滤波器仍然是一个强大的工具。