序列机器人链中关节2后置位移的计算

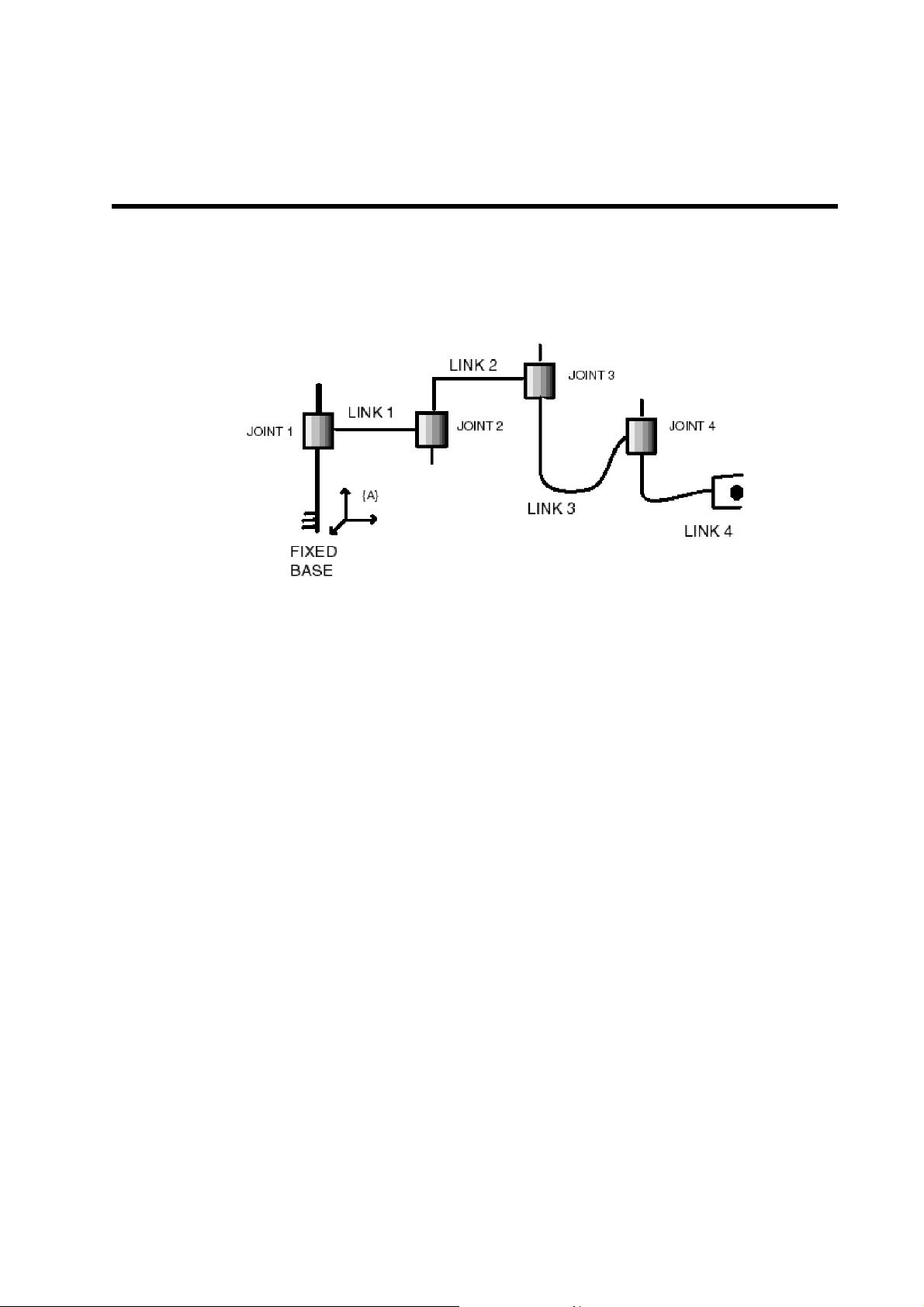
在"CS223A Introduction to Robotics"这门课程的冬季2007/2008年的第二份家庭作业解答中，讨论的是一个通用的开放型、串联（serial）的机械臂（arm）的运动学问题。这个机械臂由多个关节（kinematic joints）组成，每个关节连接着相邻的两个部件。关节之间的相对位移由一个4x4矩阵T描述，矩阵元素是在基座（base）固定坐标系{A}中计算的。 问题的核心是理解关节间运动的顺序对整体位移矩阵的影响。当关节的位移按照序列1、2、3、4进行时，即从自由端（free end）开始逐个移动，总位移的表示为T1 * T2 * T3 * T4。这里的T1到T4代表了每个关节的独立位移操作。 然而，如果关节的位移顺序反转，从固定端开始（即先执行关节4的位移），然后依次执行关节3、2和1，这时像T2、T3和T4这样的矩阵不再反映实际的位移，因为它们没有按照原定的运动路径。 题目要求根据原始的Ti来计算： (a) 当关节2的位移发生在关节1之后时，我们需要找到新的关节2位移操作的矩阵T'2。为了计算T'2，关键在于识别出这种顺序变化后，前一个关节（这里指关节1）已经完成了其位移，所以对于关节2，它实际上是在一个已知的初始位置（由T1表示）上进行的位移。因此，T'2可以看作是T1的逆运算与关节2自身的位移矩阵T2的组合，即T'2 = T1^-1 * T2。 总结来说，这个问题考察了串联机械臂中关节位移顺序对整体运动模型的影响，以及如何通过逆运算处理这种变化。理解和应用这种位移矩阵的乘法规则对于机器人运动学的理解至关重要，尤其是在设计和控制机械臂运动时，正确地考虑关节间的运动序列是不可或缺的。