树与二叉树详解：遍历、计数与应用

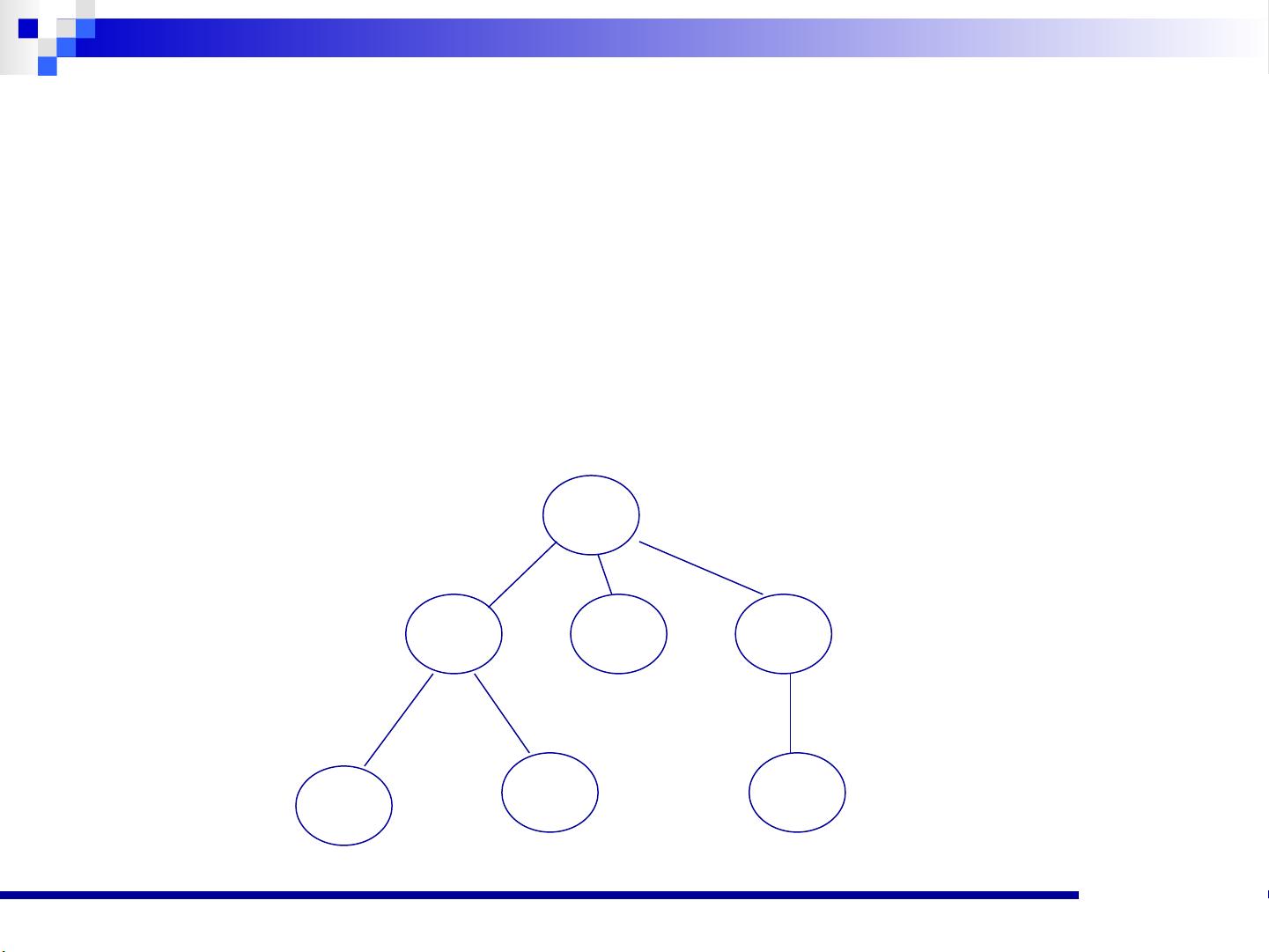
"本资源是关于数据结构中树和二叉树的全面讲解，包括了树的存储方式、链表表示、以及前序、中序、后序遍历的代码实现，同时也涵盖了二叉树的遍历、计数、线索化、树与森林的转换、堆以及Huffman树等知识点，适合学习数据结构的学员使用。" 在数据结构领域，树是一种非线性的数据结构，由n（n>0）个有限节点组成，这些节点通过边相互连接形成层次关系，每个节点可能包含零个或多个子节点。根据是否有根节点，树可以分为自由树和有根树。有根树有一个特殊的节点——根节点，其余节点分为若干子树，每个子树的根节点只有一个父节点（即根节点），但可以有零个或多个子节点。 1. 树的基本术语： - 根节点：树的顶部节点，没有父节点。 - 子节点/子女：节点的子树的根节点，成为该节点的子节点。 - 父节点/双亲：子节点的直接上级节点。 - 兄弟节点：同属一个父节点的子节点之间互称为兄弟节点。 - 度：节点的子节点数量，树的度是所有节点度的最大值。 - 分支节点/非终端节点：度不为0的节点。 - 叶节点/终端节点：度为0的节点，没有子节点。 - 祖先节点：从某个节点到根节点路径上的所有节点。 - 子孙节点：某个节点的所有子树节点。 - 层次：节点离根节点的距离，根节点层次为1，子节点层次加1。 - 深度：节点的层次，树的深度是最远叶节点的层次。 - 高度：叶节点的高度为1，其父节点高度加1，以此类推，直至根节点。 2. 二叉树： - 二叉树是每个节点最多有两个子节点的特殊树形结构，分为左子节点和右子节点。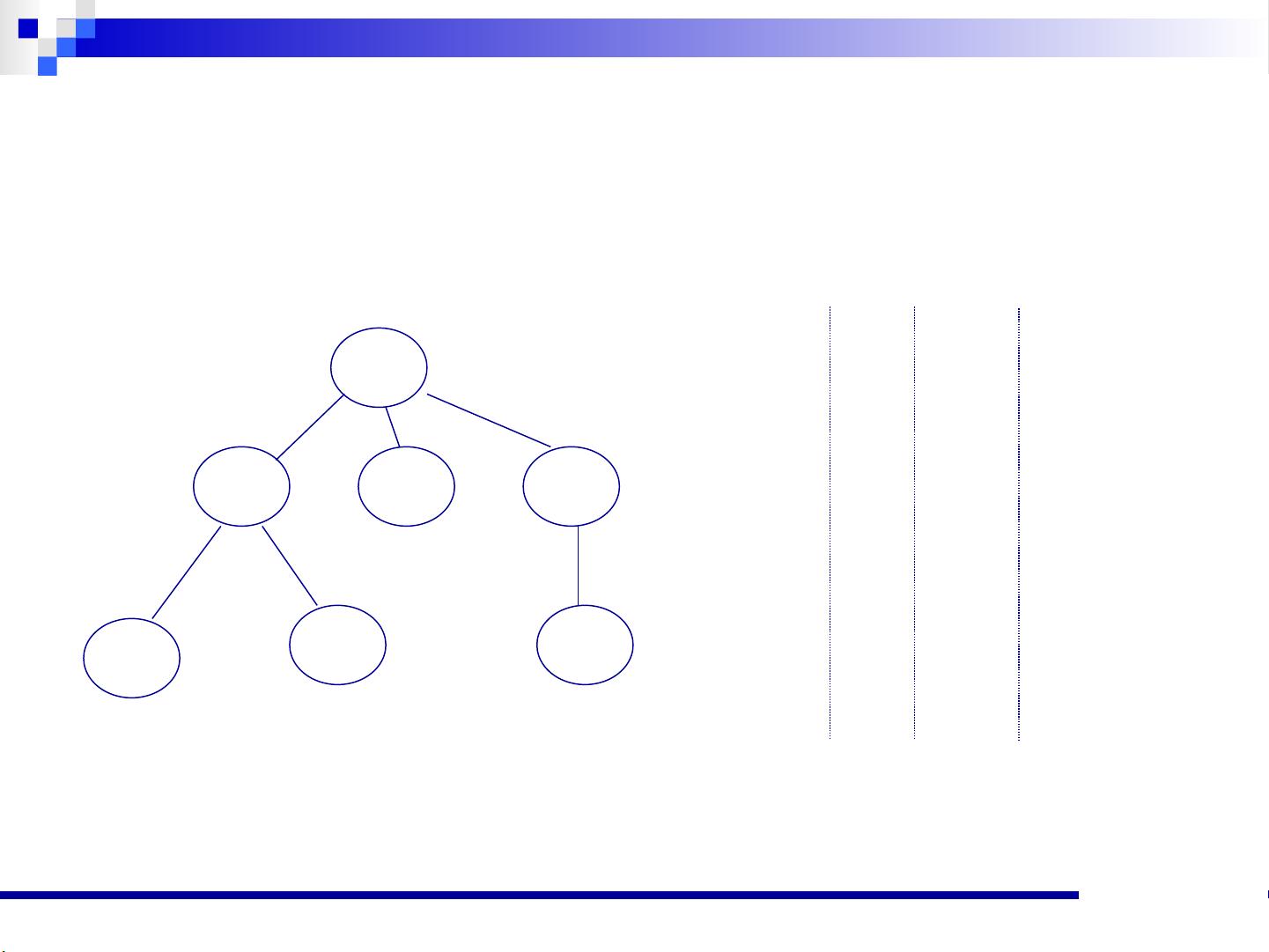 - 遍历：二叉树的遍历方法有三种，分别是前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。 3. 线索化二叉树： - 在二叉链表中添加线索，便于进行中序或其他非递归遍历。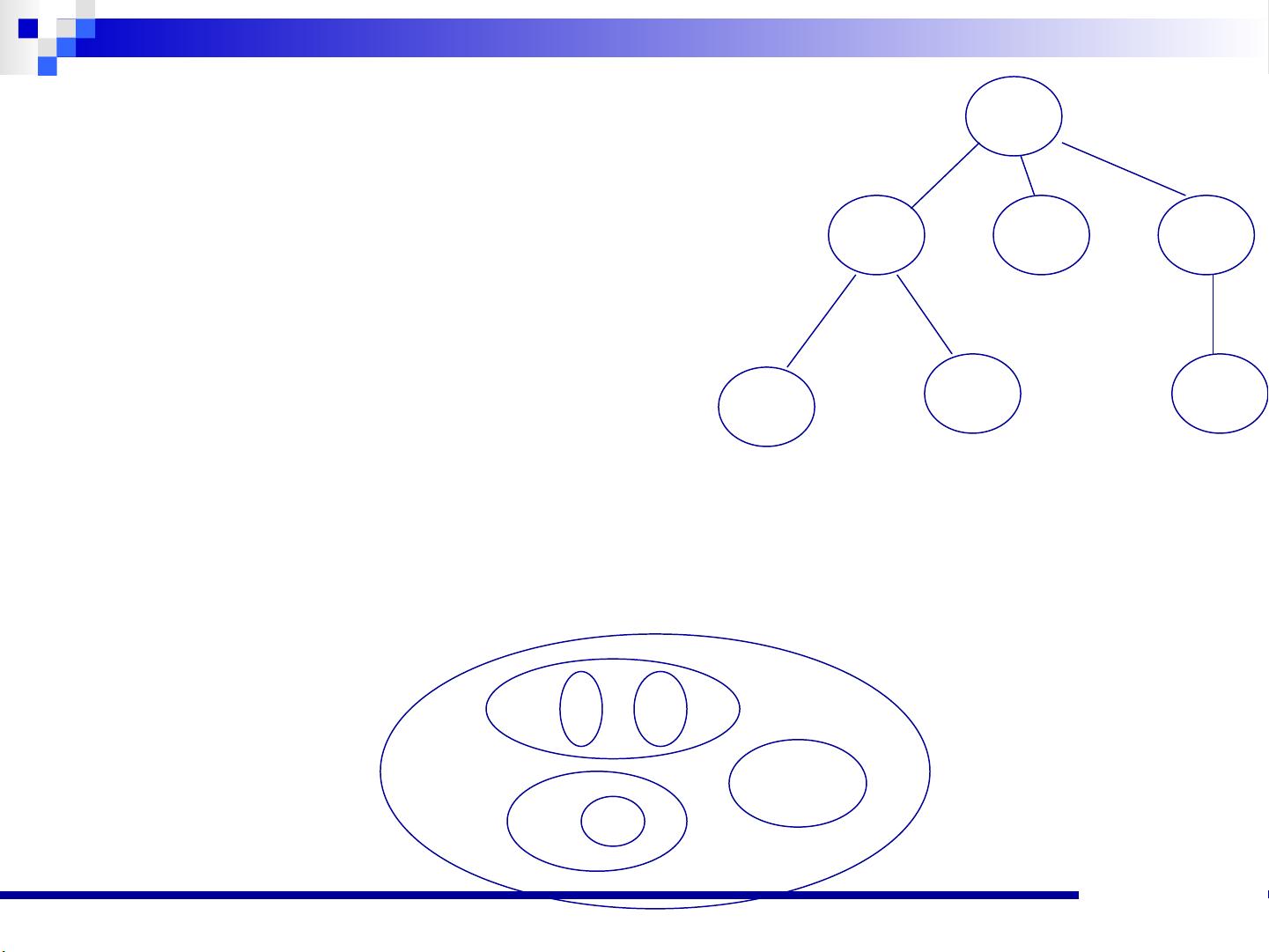 4. 树与森林： - 森林是若干棵树的集合，树与森林之间的转换有多种算法，如森林转化为二叉树等。 5. 堆： - 堆是一种特殊的树形数据结构，满足堆性质：父节点的键值总是大于或等于（最大堆）或小于或等于（最小堆）其子节点的键值。 6. Huffman树： - Huffman树是一种带权路径长度最短的二叉树，常用于数据压缩，通过贪心算法构造。 这些概念和操作在实际编程中有着广泛的应用，例如在文件系统、编译器设计、图算法优化、数据库索引等领域。了解和掌握这些知识点对于深入理解和应用数据结构至关重要。本资源提供的课件包含了这些概念的详细解释和代码实现，有助于学习者深入理解并动手实践。