离散傅里叶变换DFT详解与应用

"这篇资源是安徽工业大学的一份关于傅里叶变换的课件，主要针对研究生学习，内容涉及离散傅立叶变换(DFT)及其相关概念，包括离散傅立叶级数(DFS)、冲激抽样、离散时间信号的频谱等，并介绍了DFT的计算公式和蝶形因子。” 傅里叶变换是一种数学工具，广泛应用于信号处理、图像分析、通信等领域，用于将时域或空间域的信号转化为频域表示，从而更好地理解和分析信号的频率成分。本课件主要讨论的是在离散环境下的傅里叶变换，即离散傅立叶变换（Discrete Fourier Transform, DFT）。 离散傅立叶变换（DFT）是将有限长的离散时间序列转化为离散频率的表示。对于一个长度为N的序列{x[n]}，其DFT定义为： \[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j2\pi kn/N} \] 这里的\( X[k] \)是频率为\( k \)的离散频率分量，\( e^{-j2\pi kn/N} \)是碟形因子或旋转因子，\( j \)是虚数单位，\( N \)是序列的长度。 DFT的结果\( X[k] \)提供了序列在不同频率上的幅度信息。逆离散傅立叶变换（IDFT）则可以将频域表示转换回时域序列： \[ x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{j2\pi kn/N} \] 离散傅立叶级数（DFS）是DFT的一个特例，当序列是周期性的，DFS可以表示为： \[ x[n] = \sum_{k=-\infty}^{\infty} X[k] \cdot e^{j2\pi kn/N} \] 其中，\( X[k] \)是DFS系数，\( N \)是序列的周期。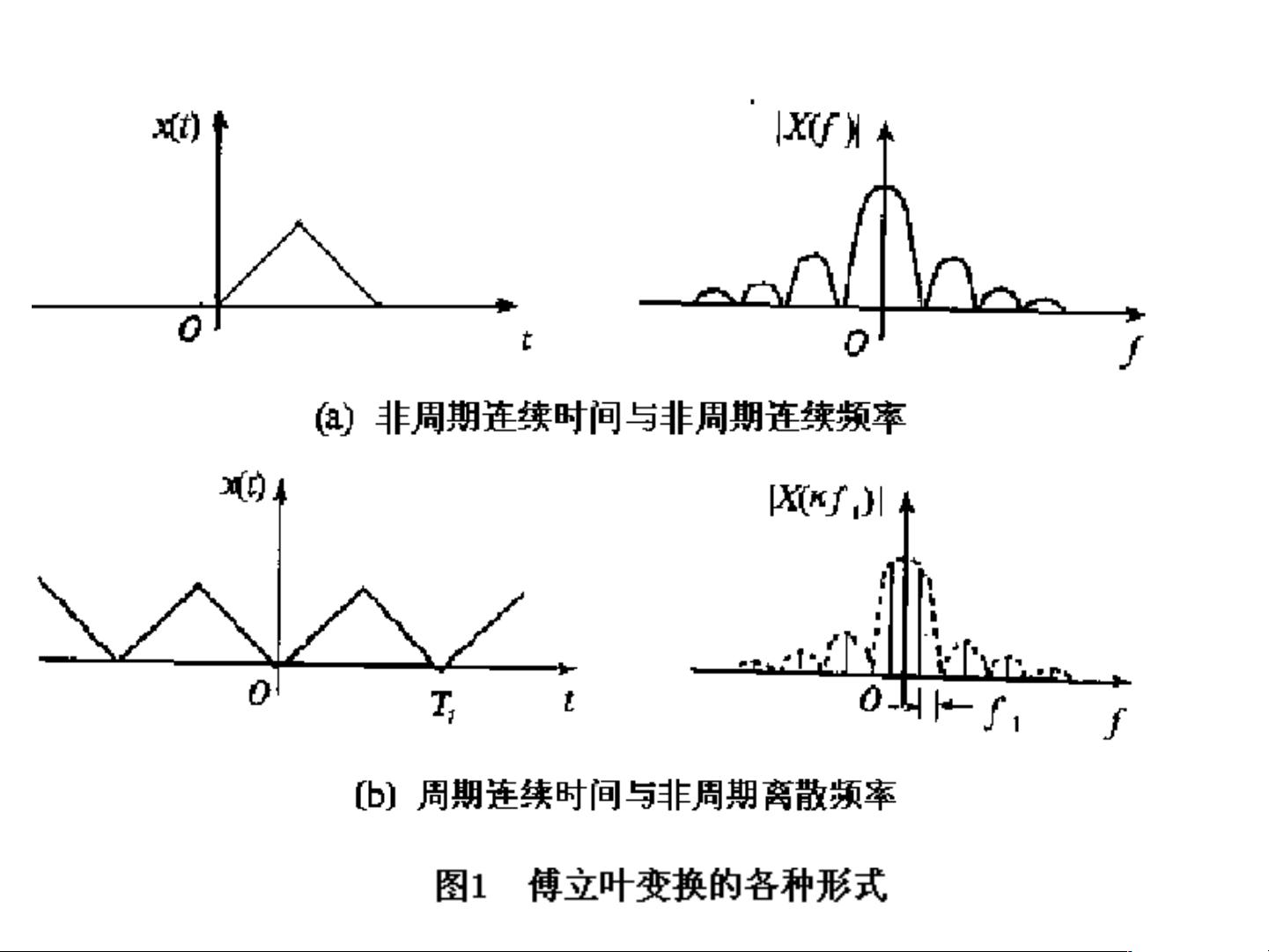 冲激抽样是将连续时间信号通过周期性地取样得到离散时间信号的过程。对于周期连续时间信号\( x(t) \)，在抽样频率\( fs \)下，其频谱会变成离散的，且以抽样频率的倒数为间隔重复。 对于周期的离散时间信号，其频谱也是离散频率的周期函数，这反映了离散时间信号的频率特性。 这份课件详细讲解了傅里叶变换在离散环境中的应用，涵盖了从理论到实际计算的多个方面，对于深入理解离散信号的频域分析具有重要意义。对于研究生或者相关领域的学习者来说，是一份非常有价值的参考资料。