主成分分析详解：理论介绍与实际应用实例

主成分分析理论介绍及举例ppt 主成分分析（Principal Component Analysis, PCA）是化学计量学（Chemometrics）中的一个重要工具，它是一种统计方法，用于处理多变量数据，特别针对数据集中的共线性和复杂性。化学计量学是一门结合了数学、统计学及其他逻辑方法的学科，旨在设计优化测量程序、实验设计以及通过分析化学数据获取最大相关信息。 在实际应用中，当我们面对的是单变量数据，比如温度、压力、pH值或单波长的吸光度等简单数值，分析仪器的高性能化如UV-可见光谱、红外(IR)、近红外(NIR)、荧光光谱、气相色谱(GC)、液相色谱(LC)、质谱(MS)以及核磁共振(NMR)等测量结果，这些数据通常是独立的单变量分析。然而，当涉及到样品-浓度、样品-变量-时间等多维度数据时，主成分分析就显得尤为重要。 在数据分析过程中，主成分分析首先通过测定收集大量数据，然后对数据进行预处理，如标准化或归一化，以便消除量纲影响。接着，PCA通过线性变换将原始的多变量矩阵转化为一组新的主成分，这些主成分是原始变量的线性组合，但保留了原数据的主要变异信息。第一主成分通常对应于数据集变异最大的方向，后续的主成分则按变异程度递减。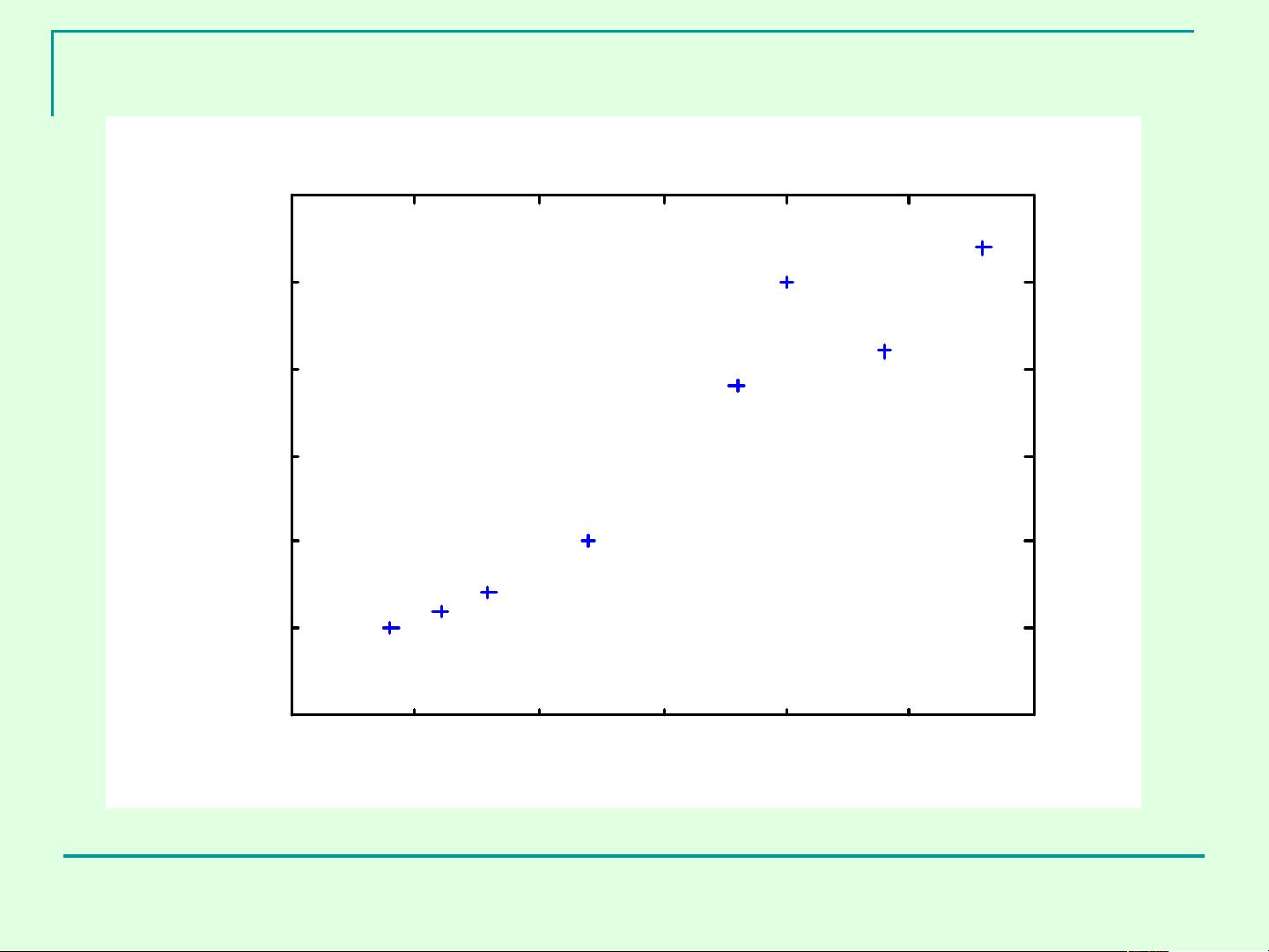 PCA的主要优点包括： 1. 数据简化：通过降维，可直观地展示高维数据在二维或三维空间的分布，便于理解和解释。 2. 抽象因子提取：主成分可以被视为数据背后的潜在结构或特征，帮助我们理解变量间的复杂关系。 3. 解决共线性问题：对于高度相关的变量，PCA能够有效地减少计算中的误差，避免因变量之间强烈相关导致的模型不稳定。 4. 稳定性提高：PCA在处理数据时具有较高的鲁棒性，能降低因数据噪声或异常值引起的不准确性。 PCA的应用范围广泛，包括但不限于： - 定性分析：用于样本分类和判别，帮助识别不同的数据类别。 - 定量分析：如工作曲线法、多元校正技术，以及在定量结构活性关系(QSAR)模型中用于变量筛选和参数估计。 - 回归分析：主成分回归(PCR)和偏最小二乘回归(PLSR)等多元线性模型中，主成分被用作输入变量，以提高预测精度。 - 预测：通过对已有数据的PCA分析，可以预测未知样品的性质或响应，如在化学合成或环境监测中的应用。 总结来说，主成分分析是化学计量学中的核心工具，通过有效地处理和分析多变量数据，为我们揭示数据背后的关键信息，提升实验设计和数据分析的效率与精度。无论是单变量数据的拓展，还是多维度数据的简化和解释，PCA都是不可或缺的技术手段。