数值计算第二章：方程求解方法

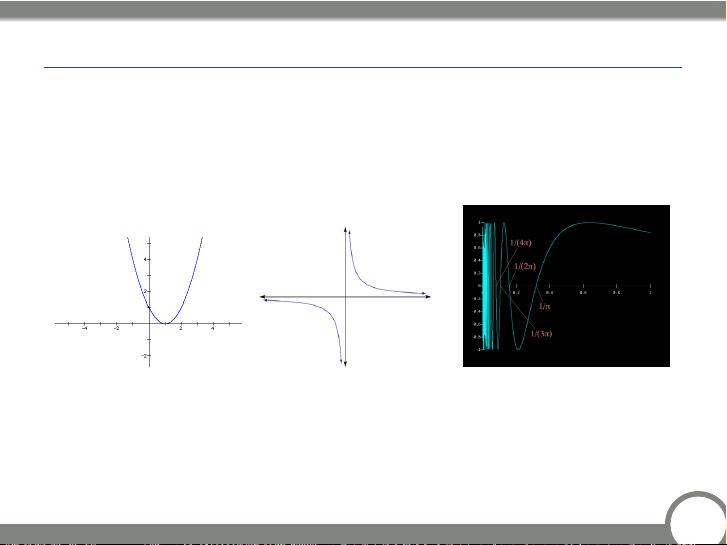
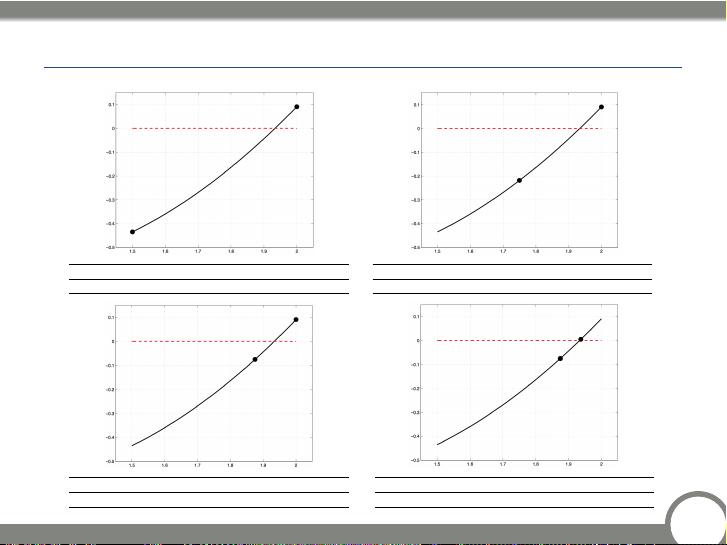
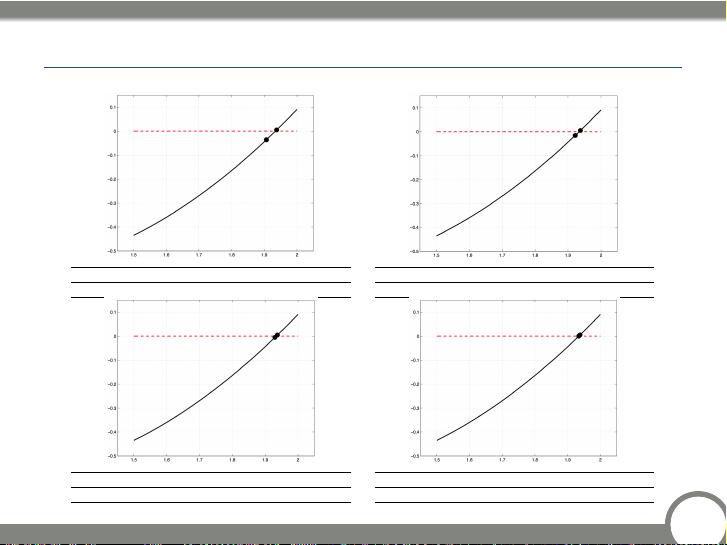
"数值计算第二章节ppt" 在数值计算这一领域，第二章节主要涵盖了求解一元方程的方法，包括引言、二分法、固定点迭代、牛顿法及其拓展以及迭代方法的误差分析。这些内容是理解数值计算基础的重要组成部分。 首先，引言部分提到了根查找问题，即寻找函数f(x) = 0的根，其中f是实值函数，根p满足f(p) = 0。这种问题在数值分析中非常基础，特别是在处理无法获得封闭形式解的复杂函数时。 二分法（Bisection Method）是求解方程的一种简单而稳健的方法。算法的基本思想是将初始区间不断对半分割，直到找到满足一定精度要求的根。二分法的特性包括其在每次迭代中都能确保目标根位于新的子区间内，因此它是一种全局收敛的方法。停止准则通常设定为区间长度小于某个预先设定的阈值或者达到最大迭代次数。 固定点迭代（Fixed-Point Iteration）是另一种求解方法，它的动机是将根查找问题转化为寻找使f(x) = g(x)的x值，其中g是一个连续且在根附近单调的函数。固定点定理保证了如果g满足一定的条件，迭代会收敛到方程的根。除了基本的固定点迭代，还有其他替代算法，如迭代公式改进或结合其他方法，如拟牛顿法。 牛顿法（Newton's Method）是数值分析中的一个强大工具，适用于求解导数可得的函数的根。牛顿法通过迭代公式x_{n+1} = x_n - f(x_n) / f'(x_n)逼近根，具有较高的收敛速度。当函数的导数信息可用时，牛顿法通常是首选。此外，还有牛顿法的变种，如割线法（Secant Method）和假位法（Method of False Position），它们在无法直接获取导数或导数难以计算时使用。 最后，误差分析是评估和控制迭代方法性能的关键部分。收敛阶（Order of Convergence）用来描述方法收敛速度的快慢，例如，一次收敛意味着每次迭代后误差减少大约一半。对于牛顿法和固定点迭代，讨论了它们在不同条件下的收敛性质，包括对多重根的处理。在处理具有多重根的问题时，需要特别注意收敛行为和选择适当的初始猜测。 这个第二章节的PPT深入讲解了数值计算中求解一元方程的基本方法和理论，对于理解和应用数值计算技术至关重要。