网络流算法详解：概念、术语与可行性条件

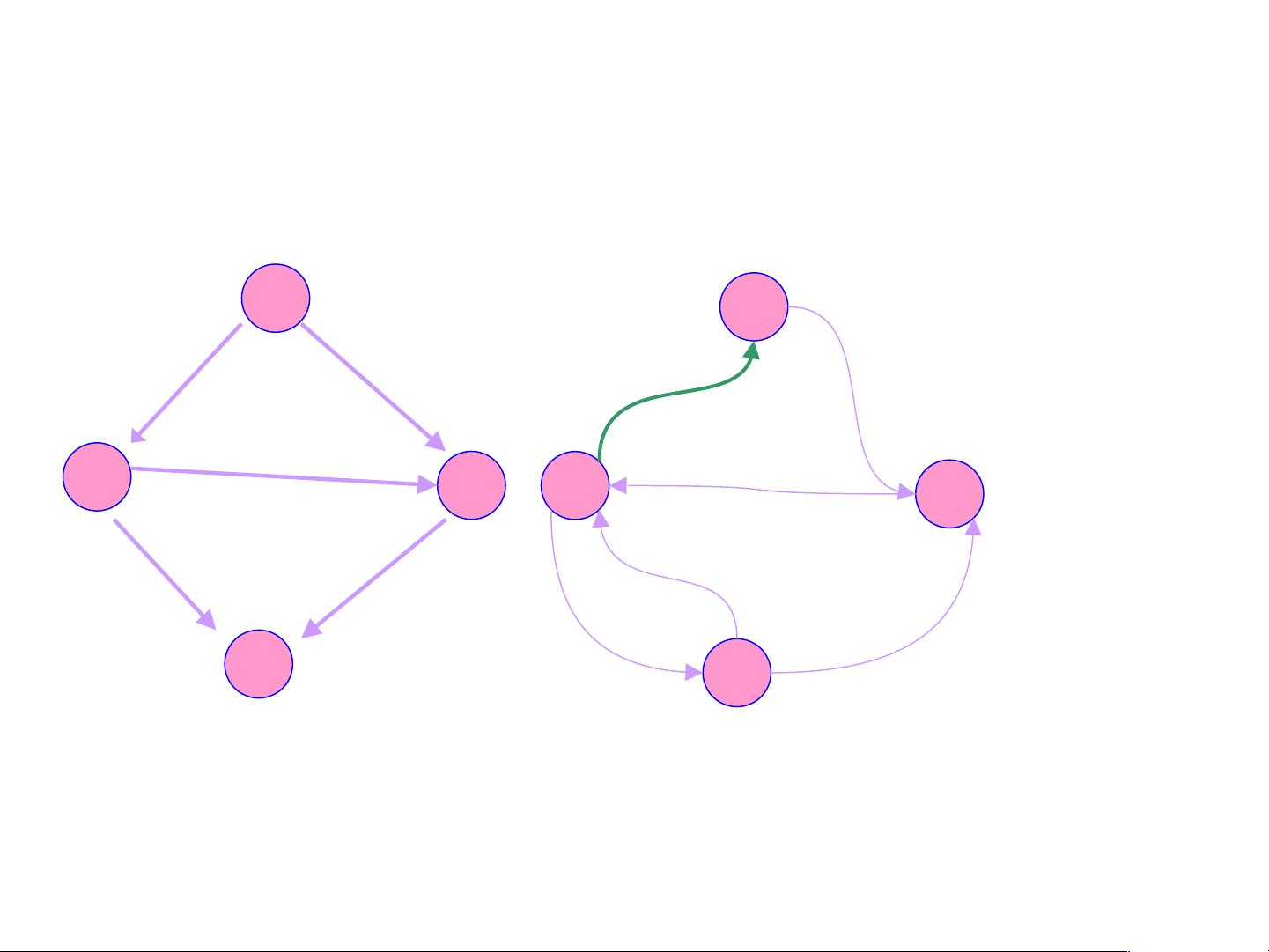
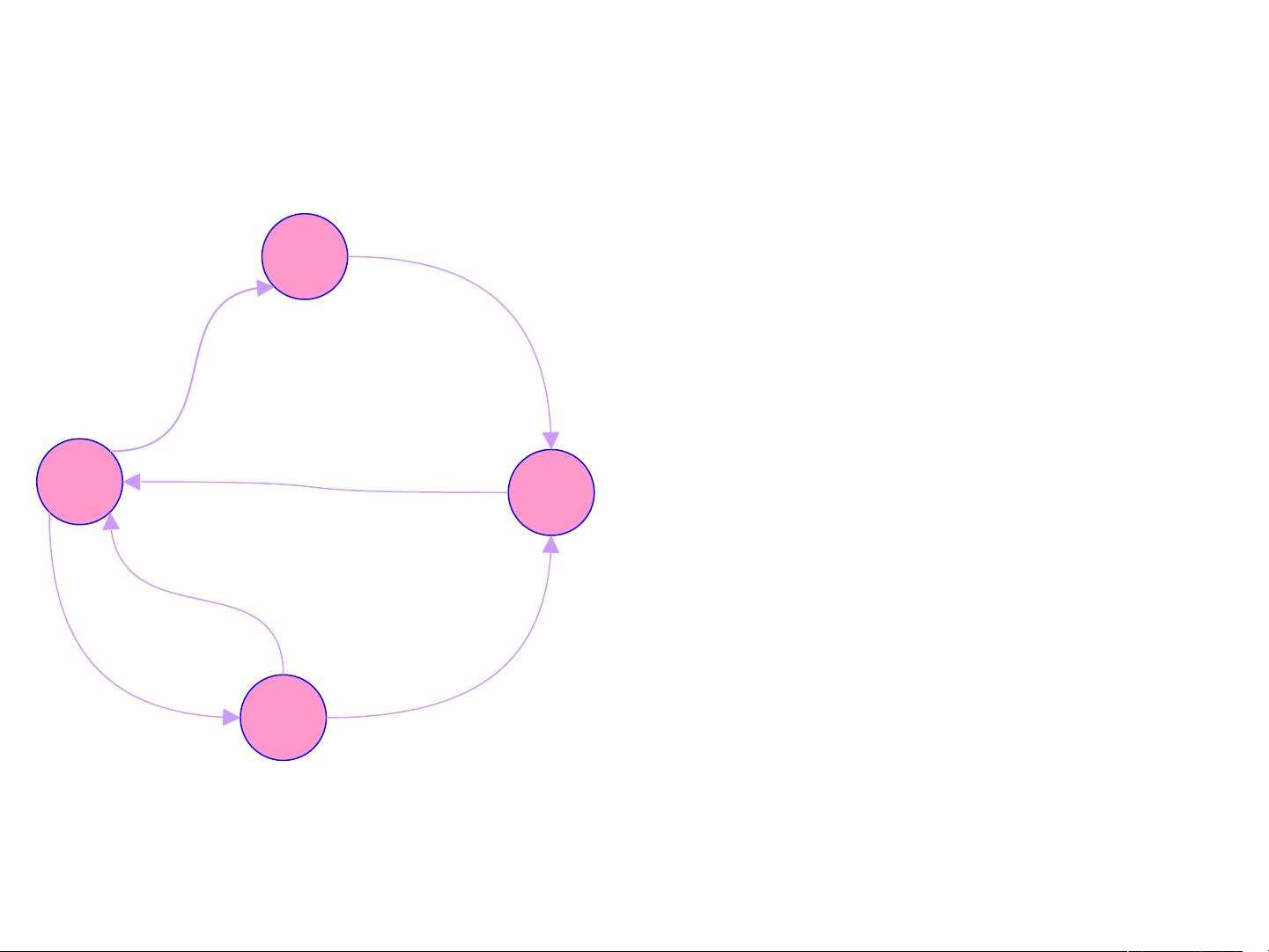
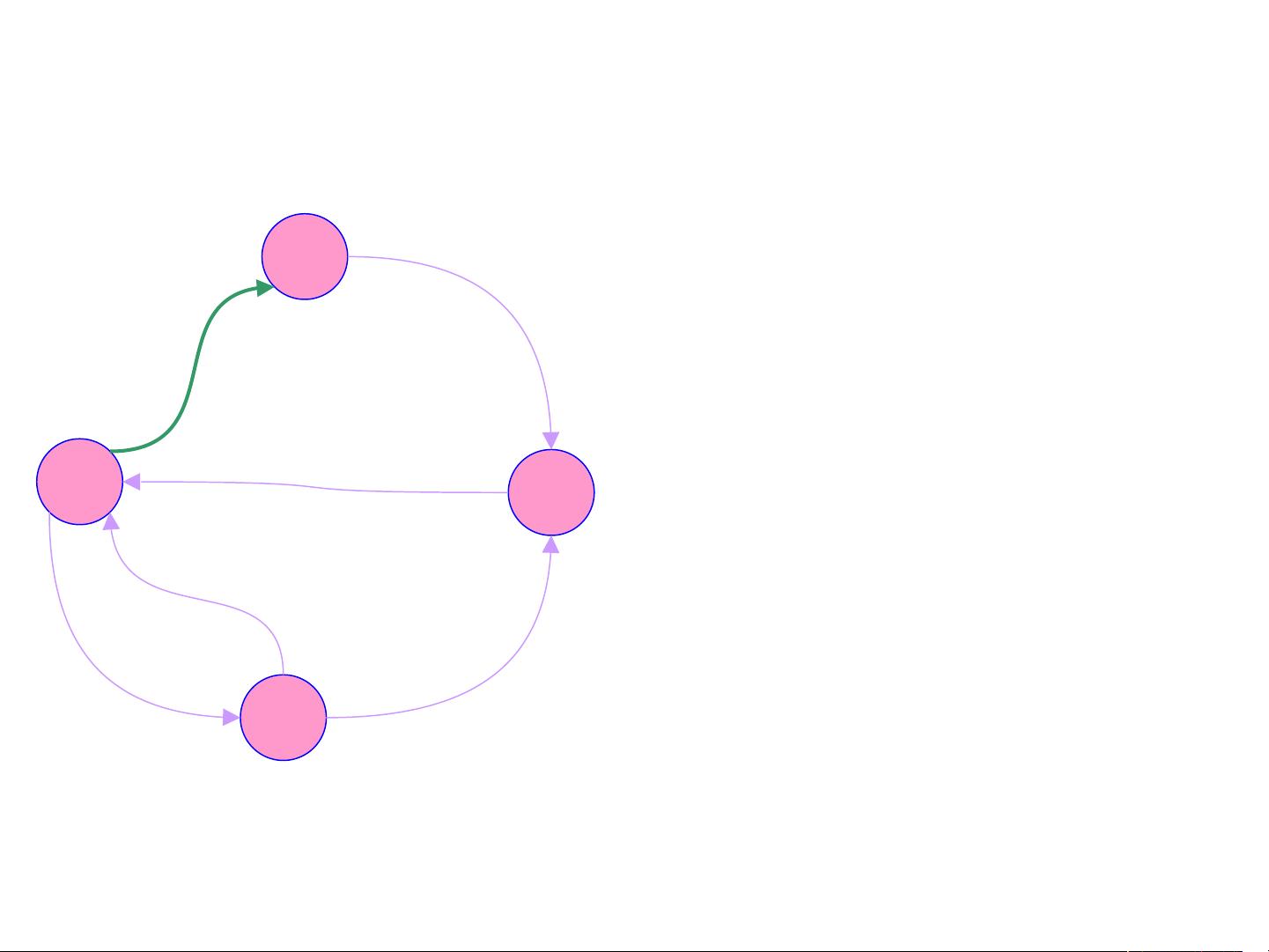
网络流算法是一种在图论中用于解决流量分配问题的重要工具，它主要应用于优化问题，特别是在计算机科学和运筹学领域。该算法关注于在一个有向图G=(V,E)中，如何有效地分配流量，使得流量从指定的源(s)流向汇(t)的同时，满足特定的容量和平衡约束。 在定义中，我们有以下几个关键概念： 1. **节点和边集** (Nodes and Edges): V代表图中的所有节点集合，E则是所有边的集合。网络中的每个边(u,v)都有一个容量c(u,v)，它定义了这条边能够承载的最大流量，且默认值为非负。 2. **源点和汇点** (Source and Sink): 指定的s是网络的起始点，t是终点，流量从s流入，经过一系列节点后最终流向t。 3. **网络流** (Network Flow): 流量flow是一个定义在边集合E上的非负函数，flow(v,w)表示边(v,w)上的流量。一个流必须满足容量约束和平衡约束。 - **容量约束** (Capacity Constraint): 流量不能超过边的容量，即0≤flow(v,w)≤cap(v,w)。 - **平衡约束** (Flow Conservation): 图中每个节点除s和t外，流出的流量等于流入的流量。对于源s，流出流量等于净输出量f；对于汇t，流入流量等于净输入量f。 4. **饱和边** (Saturated Edges): 当流量达到边的容量时，这条边被称为饱和边，即flow(v,w)=cap(v,w)。 5. **可行性** (Feasibility): 只有当流量分配满足上述所有条件时，才称其为可行流。0流是一个特殊的可行流，其中所有边的流量都为0，流量总量为0。 网络流算法的主要目标是找到一个最大的流量值，使得源点和汇点之间的流量传输达到最优，同时满足所有边的容量限制。常见的网络流算法包括 Ford-Fulkerson 算法、Edmonds-Karp 算法和 Dinic's Algorithm等，它们通过迭代的方式逐步增加流量，直到达到容量限制或者找不到增广路径为止。这些算法在许多实际问题中扮演着核心角色，如电路设计、运输问题、数据通信等领域。