差分演化算法：一种高效全局搜索工具

"差分演化算法" 差分演化算法（Differential Evolution, DE）是一种基于群体的全局优化方法，由R. Storn和K. V. Price在1995年为解决切比雪夫多项式拟合问题而提出。这种算法的核心在于其简单、高效和鲁棒的特性，使得它在复杂优化问题中展现出强大的适应性和解决能力。差分演化算法采用实数编码，通过向量差分策略进行种群更新，主要遗传操作是差分变异算子。 差分变异算子是DE的关键创新，它通过对个体之间的向量差分进行运算，产生新的候选解，以此探索解决方案空间。这个过程不仅保留了原有的优秀特性，还引入了新的变化，从而提高了算法的探索能力。在1996年的第一届国际演化计算竞赛中，DE获得第三名，尽管不是第一名，但因其实际应用潜力，逐渐受到研究者关注。 DE算法的简单性和易用性使得它在工程领域广泛应用。为了推广DE，Storn和Price创建了算法的官方网站，提供多种编程语言的源代码，包括C、C++、Java、Matlab、Fortran90和Python等，这极大地推动了DE的理论研究和实践应用。网站上的资源不仅方便了初学者学习，也为专业工程师实施优化任务提供了便利。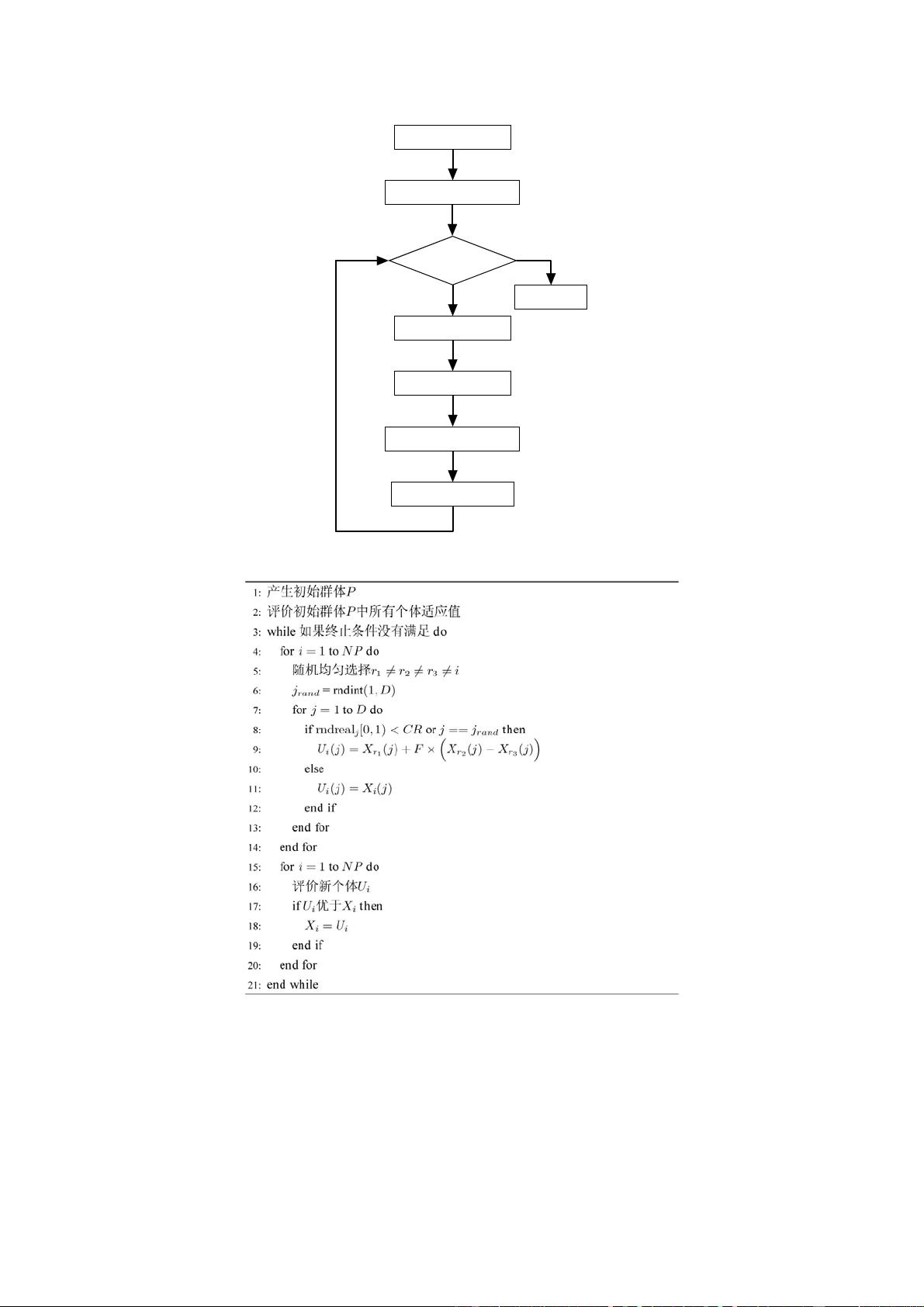 DE算法的结构主要包含以下部分： 1. 初始化阶段：创建一个随机初始种群，每个个体代表一个可能的解决方案。 2. 差分变异：选择三个个体，计算它们的差分，然后将这个差分与第四个个体相加，生成新的候选解。 3. 选择策略：根据某种适应度函数，比较新旧个体，保留较优的个体，形成下一代种群。 4. 终止条件：当达到预设的迭代次数、目标精度或其他终止条件时，算法停止，输出当前最优解。 差分演化算法的鲁棒性体现在它对初始种群和控制参数的选择不敏感，能够在各种复杂优化问题中表现出稳定性能。此外，DE的并行化特性使其在大规模问题和高维空间中表现优越，因为可以利用多核处理器或分布式计算资源加速求解过程。 DE算法的这些优势使得它在工程优化、机器学习模型参数调优、信号处理、控制工程、经济建模等多个领域都有广泛应用。然而，选择合适的参数设置（如种群规模、变异因子、交叉概率等）仍然是影响DE性能的重要因素，研究人员和实践者需要根据具体问题调整这些参数以达到最佳效果。 差分演化算法以其独特的设计和优异的性能，在全球优化领域占据了一席之地，并且随着研究的深入和算法的不断改进，其在未来将继续发挥重要作用。