理解Bayesian博弈：不完全信息的游戏

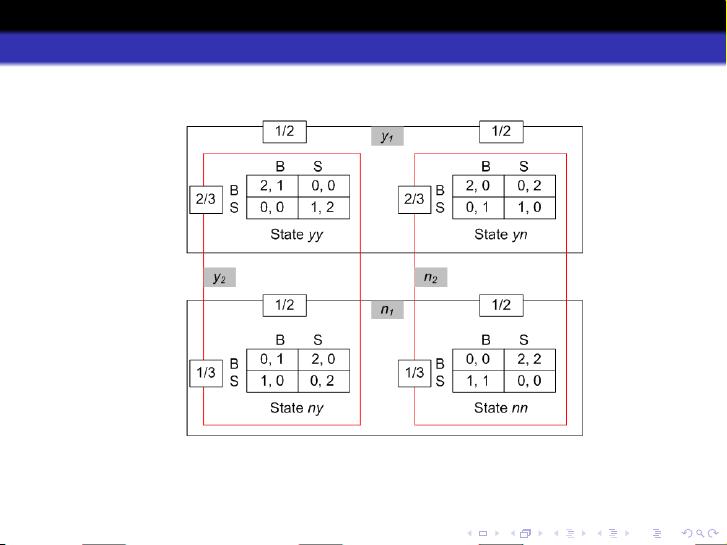
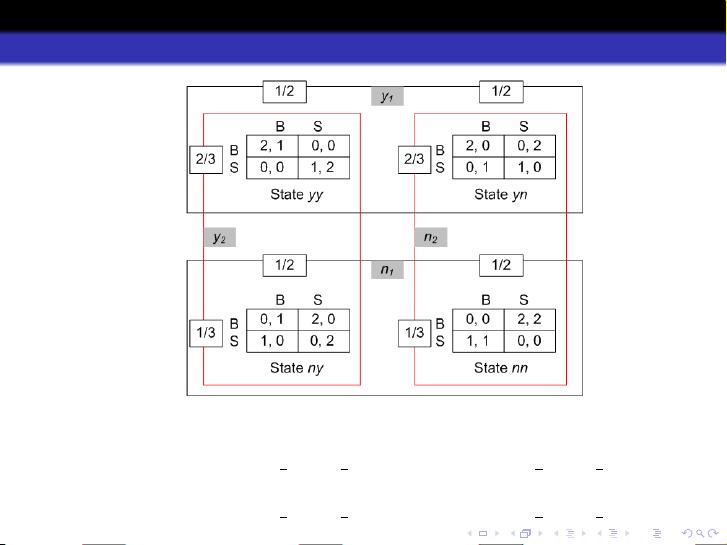
"这篇资料主要介绍了贝叶斯博弈（Bayesian Games）理论，它是博弈论的一个分支，特别关注不完全信息的情况。在这些游戏中，至少有一方并不完全了解其他参与者的所有偏好或相关特性，形成了不完全信息博弈。资料中提到了贝叶斯定理的应用，并通过一个例子——一方不确定另一方是否希望见面的博奕变体，来阐述这种理论。" 贝叶斯博弈理论是博弈论中的一个重要概念，它扩展了传统博弈论的框架，引入了不完全信息的概念。在传统的博弈论中，所有玩家都对其他玩家的偏好和收益函数有完整的了解，即博弈是完全信息的。然而，在现实生活中，这种情况往往并不常见。贝叶斯博弈考虑了信息不对称的情况，其中一个或多个玩家可能对某些关键信息有所保留或者不了解。 贝叶斯定理在这里起到了关键作用，它是一种概率推理方法，用于更新先验概率以反映新的观察数据。在不完全信息的博弈中，玩家需要根据已有的信息和游戏过程中的新发现，不断调整他们对其他参与者类型（或策略）的信念。例如，资料中提到的例子中，玩家1不知道玩家2的真实意愿，只能基于一定的概率假设进行决策。玩家2有两种类型，每种类型的出现概率相等，这促使玩家1必须采取一种混合策略，以应对可能的情况。 在游戏开发和其他领域，贝叶斯博弈的应用十分广泛。它可以用于模拟复杂的人际互动、决策制定和策略规划。比如在游戏设计中，可以构建不完全信息的场景，增加游戏的策略性和不确定性，使玩家需要在信息有限的情况下做出最佳选择。此外，该理论还可以应用于经济学、政治学、社会学等多学科的研究，如市场预测、政策制定、司法系统（如陪审团决策过程）等领域。 学习贝叶斯博弈，不仅需要理解基本的博弈论原理，还需要掌握概率论和统计学的知识，以及如何处理不确定性。资料中提到的“Lecture Note 7: Bayesian Games”可能是一个教学章节，提供了深入探讨这一主题的材料。通过这样的学习，我们可以更好地理解和解决现实世界中那些充满不确定性的决策问题。