RMQ问题详解：三种解法与ST算法的动态规划实现

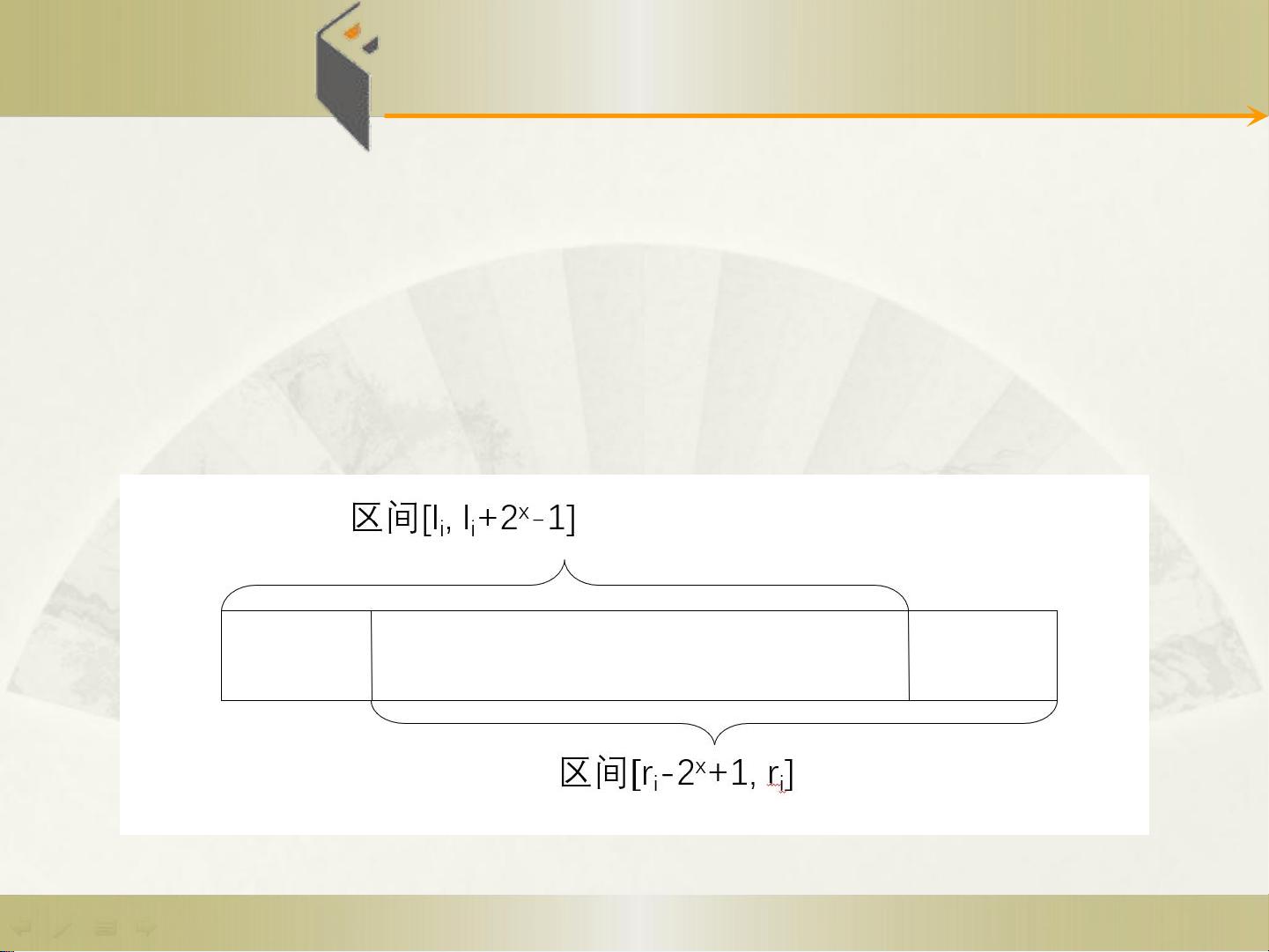
第2章RMQ-2020-12-07文档主要讨论了Range Minimum Query (RMQ)问题，这是一个常见的计算机科学问题，用于在给定一个整数数组A后，快速查询区间内的最小值。RMQ问题的关键在于设计高效的算法来处理大量的查询请求，同时保持低的预处理时间和查询时间。 文档首先介绍了RMQ的基本概念，指出它在实际应用中常用于需要频繁查询区间最大值或最小值的场景。三种主要的解法包括： 1. **朴素方法**（也称为搜索法）：这种方法通过遍历数组来寻找指定区间的最小值，其预处理时间为O(n)（n为数组长度），查询时间为O(n)，不适合大量查询。 2. **线段树**（Segment Tree）：线段树是一种数据结构，它将数组划分成多个子区间，每个节点代表一个区间。通过构建树状结构，可以将查询复杂度降低到O(logn)，预处理时间为O(n)，适用于对区间查询有较高效率的需求。 3. **ST算法（Segment Tree）**：这是文档的重点，实际上是一种动态规划的应用，也是解决RMQ问题的一种高效方法。ST算法的特点是预处理时间复杂度为O(nlogn)，查询时间复杂度仅为O(1)。它利用了递归的思想，通过“倍增”计算，f[i][j]表示从i到i+2^j-1范围内的最大值，通过分治策略将区间缩小，直至达到基本操作。ST算法适用于查询次数非常多且没有修改需求的场景。 文档还详细解释了ST算法的流程，包括预处理阶段，其中构建ST数据结构的过程，以及如何根据这个结构在O(1)时间内找到区间内的最大值。预处理阶段涉及将数组划分并存储最大值，如将f[i,j]拆分为f[i,j-1]和f[i+2j-1,j-1]，以便后续查询。 第2章RMQ-2020-12-07文档提供了RMQ问题的基础知识，重点阐述了ST算法的实现细节和适用场景，对于理解和应用区间最值查询具有较高的参考价值。