平衡二叉树与AVL树详解

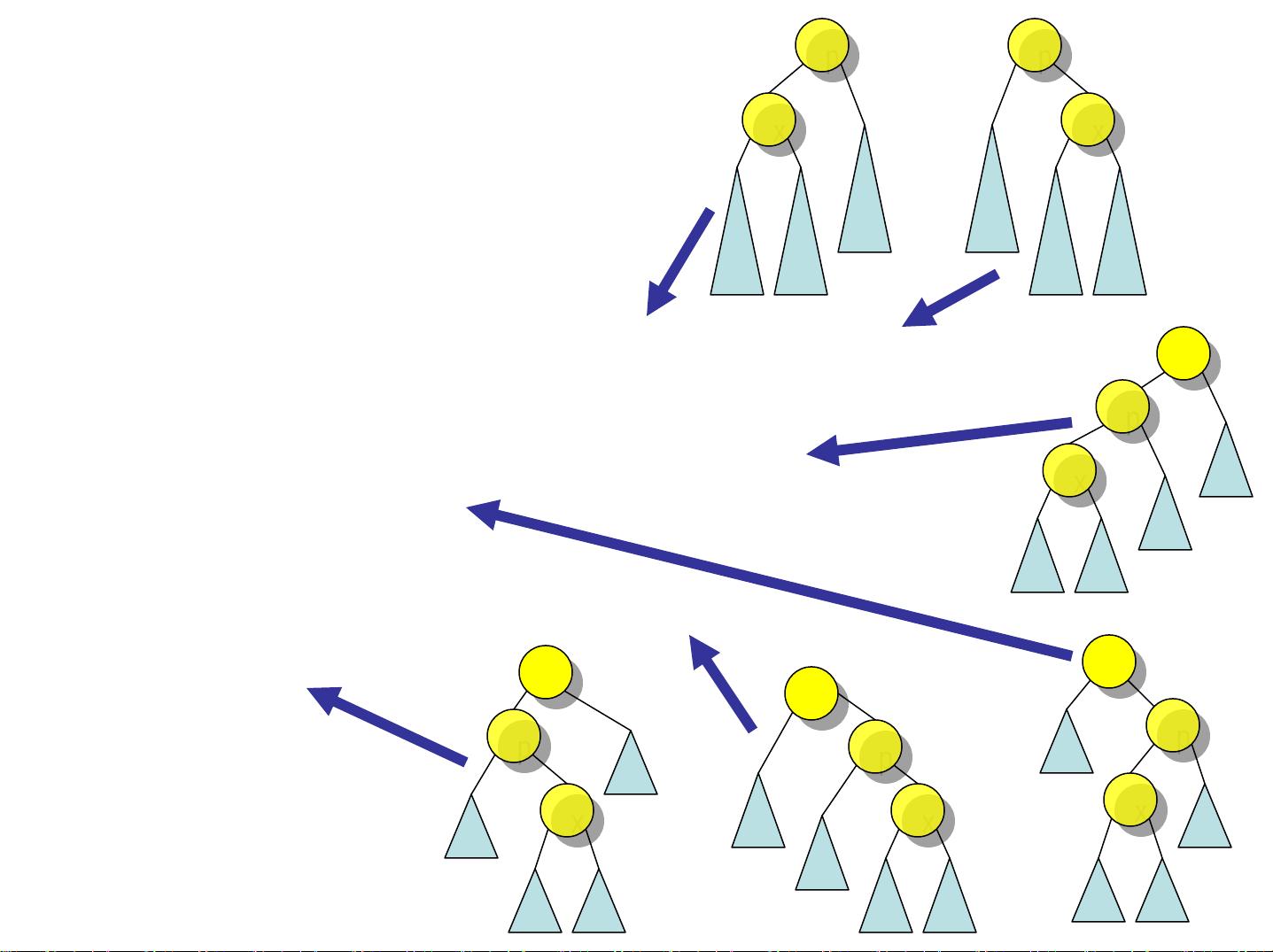
"这篇内容主要介绍了高级数据结构中的平衡二叉树，特别是AVL树的概念、性质以及旋转操作。" 在计算机科学中，高级数据结构是处理复杂数据组织方式的关键，其中平衡二叉树是一种重要的数据结构，它优化了基本二叉搜索树（BST）的性能。基本BST遵循左子节点小于根节点、根节点小于右子节点的规则，并通过递归定义保证了树的结构。在BST中，查找、插入和删除操作的时间复杂度与树的高度有关。理想的树应该是平衡的，即树的高度为O(logn)，这样可以保证操作效率。然而，如果不进行平衡处理，树可能会退化成链表形式，导致高度为O(n)，从而严重影响性能。 平衡二叉树的一个经典实例是AVL树，由Adelson-Velsky和Landis于1962年提出。AVL树是一种特殊的二叉排序树，其定义是每个节点的左右子树高度差不超过1。这个特性确保了AVL树的平衡性。为了保持这种平衡，AVL树引入了旋转操作：当插入或删除节点导致不平衡时，可以通过单旋转或双旋转来调整树的结构。单旋转包括右旋和左旋，双旋转则是在单旋转的基础上进行组合，以恢复树的平衡。 例如，如果一个节点的右子树过高，可以执行右旋操作，将右子树的根节点提升到父节点的位置，而父节点则下移为右子节点。若不平衡情况更复杂，可能需要先对父节点的左子树进行左旋，然后再对父节点进行右旋，以解决祖父节点与孙子节点不共线的情况。 AVL树的插入算法通常从插入元素开始，然后自底向上遍历，直到找到第一个不平衡的节点，即“祖父”节点。这个节点的父节点被称作“父”节点，而新插入的节点可能是导致不平衡的“儿子”节点。根据不平衡的类型，执行相应的旋转操作以重新平衡树。通过这种方式，AVL树能够保证在最坏情况下的查找、插入和删除操作都具有O(logn)的时间复杂度。 除了AVL树，高级数据结构还包括其他平衡树如红黑树、B树、B+树等，以及可并优先队列、线段树和树状数组等高效的数据结构，它们各自在不同的场景下有着广泛的应用。理解并掌握这些高级数据结构对于提升算法效率、优化程序性能至关重要。