博弈论学习资源与SG函数模板解析

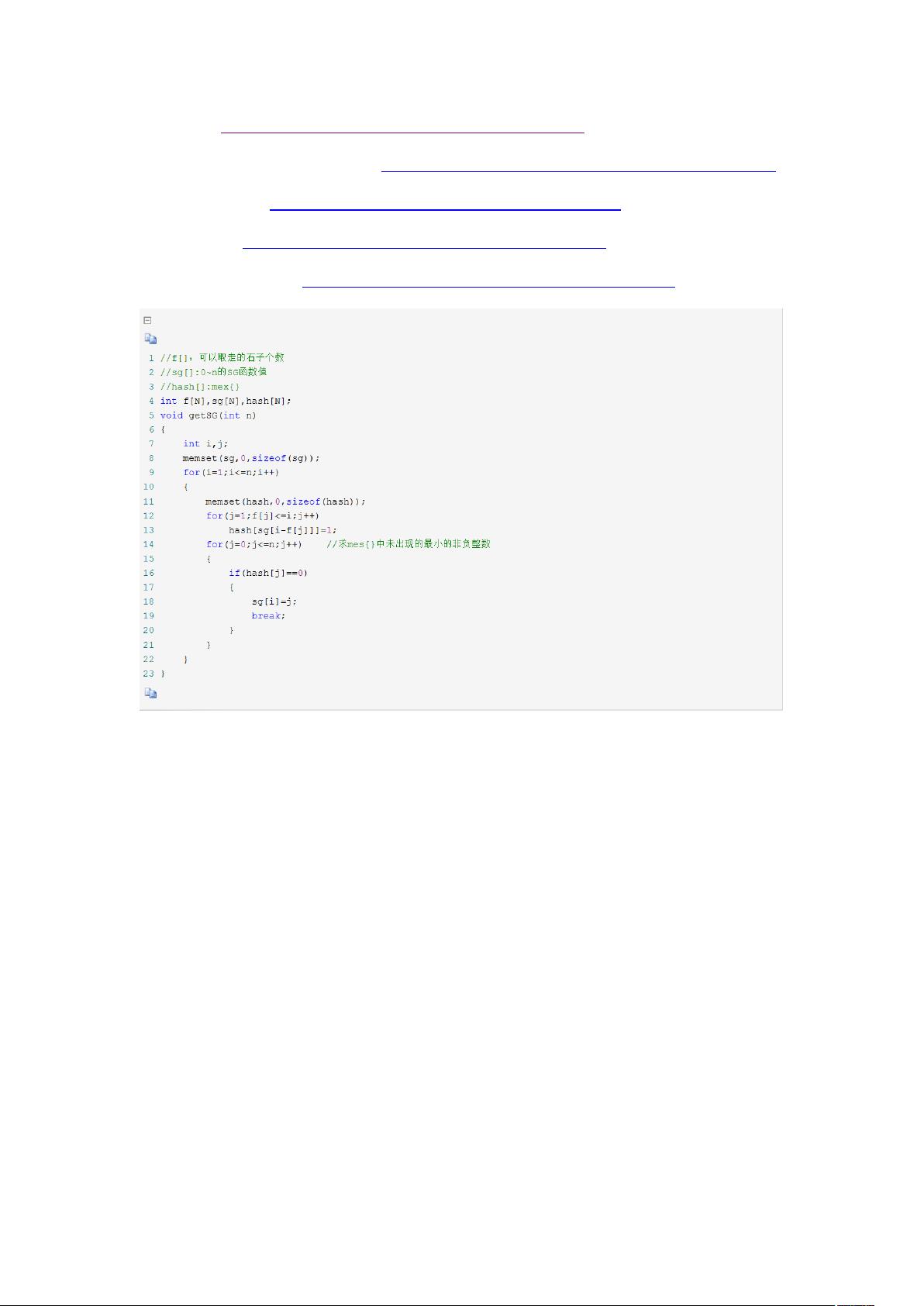
该资源主要涉及博弈论在编程中的应用，特别是通过Java语言解决博弈问题。提供的链接包括博弈论的SG函数详解、题型总结以及石子类问题的解析。代码段展示了如何初始化并计算SG函数，其中包含了几个常见的编程错误示例。 博弈论是一种应用于决策科学的数学理论，它研究在零和游戏中（即一方获利必然导致另一方损失）的策略选择。在编程中，博弈论常常用于解决一类问题，如石子游戏、棋盘游戏等，通过计算某些特定函数（如SG函数）来确定游戏的获胜策略。 1. SG函数详解： SG函数（Solving Game Function）是博弈论中的一个重要概念，用于表示某个状态下玩家能获得的最好结果。对于一个博弈问题，SG函数可以决定当前状态是否为玩家的优势状态，如果是，则玩家有策略保证不输；如果不是，则对手有策略保证不输。计算SG函数通常采用动态规划的方法。 2. 错误分析： - 错误1：在计算SG函数之前忘记初始化数组sg[]。这可能导致在计算过程中使用到未定义的值，从而导致结果错误。 - 错误2：在遍历每个状态之前忘记初始化vis[]数组。vis[]通常用于记录某个状态是否已经被访问过，若未初始化，可能造成重复计算或者丢失某些状态信息。 - 错误3：在vis[]中应该存储sg[i-F[j]]的值，而不是直接使用j。这是因为我们需要知道去掉F[j]个单位后剩余状态的SG值是否已经计算过。 3. 动态规划求解： - 在给定的代码中，`getSG`方法通过动态规划计算SG函数。首先对所有状态进行初始化，然后从最小的状态开始，逐个计算每个状态的SG值。在计算过程中，利用vis[]数组标记哪些状态已经被处理过，找到第一个未被处理的状态作为当前状态的SG值。 4. F数组： - F数组似乎是在初始化 SG 函数前的部分代码，但没有完整显示。通常，F数组可能用来存储一些基础状态或递推关系，例如斐波那契序列或其他博弈问题中的基础解。 5. 石子类问题： - 石子类问题通常涉及到两个玩家轮流从一堆石子中拿走一定数量的石子，目标可能是获取最后一颗石子或达到某个目标分数。这类问题可以通过SG函数进行求解，找出最优策略。 6. 题型总结： - 提供的链接中包含了博弈论的各种题型总结，可以帮助学习者理解不同类型的博弈问题，并提供了解决这些问题的思路和方法。 这个资源提供了学习和解决博弈问题的宝贵资料，特别是通过Java实现SG函数的方法，有助于提升编程解决复杂策略问题的能力。