支持向量机(SVM)详解：最大几何间隔与数学模型

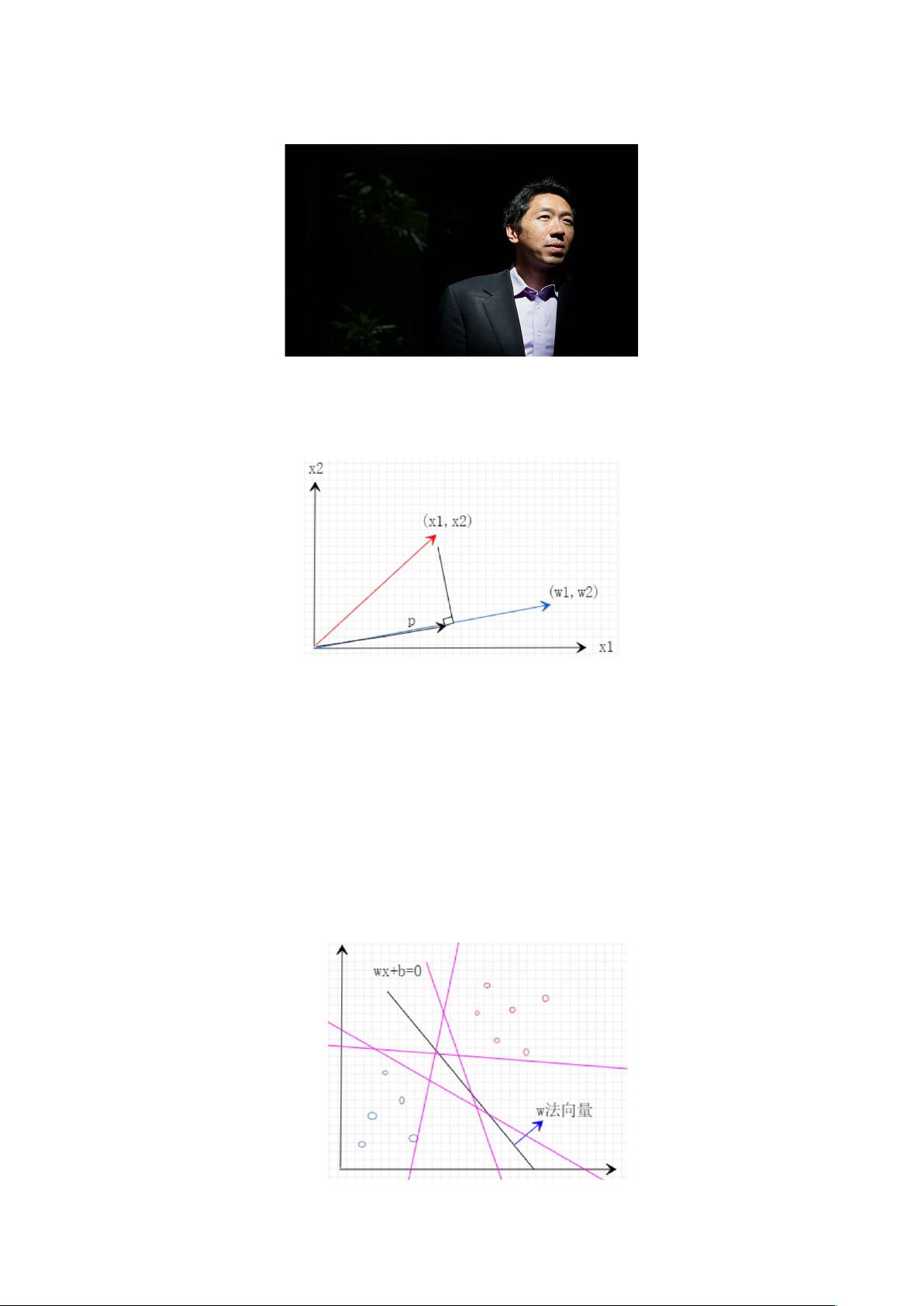
"这是关于机器学习中支持向量机(SVM)的总结，涵盖了大量计算过程和图表，旨在帮助初学者理解和掌握SVM的基本概念和原理。" 在机器学习领域，支持向量机（Support Vector Machine，SVM）是一种非常有效的监督学习算法，尤其在分类问题上表现出色。在SVM中，我们寻找的是一个能够最好地将不同类别样本分开的超平面。与感知机类似，超平面是一个高维空间中的决策边界，由权重向量w和偏置项b定义，即w·x + b = 0。 在二维空间中，w·x可以理解为向量w和x之间的内积，代表x在w上的投影的长度。感知机的分类规则是：如果w·x > 0，则样本被归类为正类，否则为负类。然而，感知机的问题在于，可能存在多个超平面可以正确地划分样本，这就引出了SVM的核心思想。 SVM的目标是找到一个能够最大化样本之间“间隔”（geometric margin）的超平面。间隔是指从最近的训练样本到超平面的距离，这提供了模型的泛化能力。理想情况下，我们希望找到一个使所有样本都远离决策边界的超平面，以便新样本出现时有更大的容错空间。因此，对于SVM，我们不仅要找到一个能正确分类样本的超平面，还要确保这个超平面具有最大的间隔。 在数学建模中，SVM引入了一个正则化参数K（在这里设定为1），使得分类条件更为严格。在训练阶段，正样本需要满足w·x + b >= 1，而负样本需要满足w·x + b <= -1。这种约束条件确保了训练样本不仅被正确分类，而且与超平面保持一定距离。这也就意味着在训练过程中，SVM会尽量扩大间隔，以提高模型的鲁棒性和泛化能力。 在实际应用中，SVM通过解决凸优化问题来找到最优的超平面，通常使用拉格朗日乘子法和软间隔概念。软间隔允许一部分样本违反分类条件，但会为此付出代价，从而平衡分类准确性和间隔最大化。此外，核技巧（如高斯核或多项式核）的应用使得非线性可分问题也能被SVM有效解决，通过在高维特征空间中构建非线性决策边界。 支持向量机通过寻找最大间隔超平面，提供了一种强大的分类方法，其在处理小样本、高维数据和非线性问题时展现出良好的性能。通过优化训练过程中的间隔，SVM能够提高模型对未知样本的泛化能力，减少预测错误。对于初学者而言，理解SVM的间隔概念、数学模型以及核函数的运用是掌握这一技术的关键。