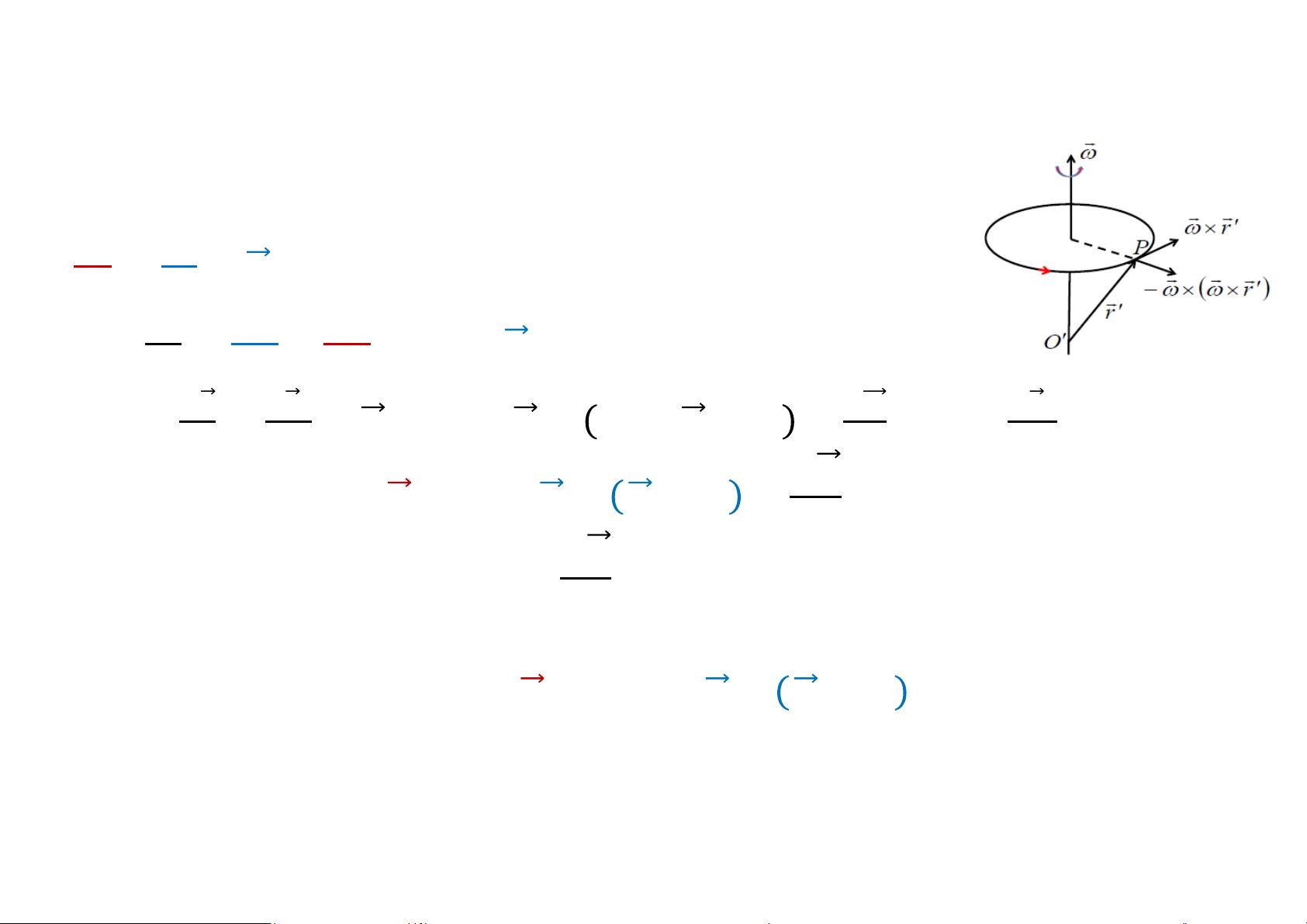拉格朗日方程：解析力学的关键与普适动力学工具

理论力学中的拉格朗日方程是一种核心概念，它在动力学研究中占据着举足轻重的地位。首先，拉格朗日方程是通过对物理系统的广义坐标和广义动量的描述，形成一组二阶微分方程，这提供了一种普适的手段来获取力学系统的动力学行为，无需依赖于特定的守恒定律。相比于牛顿力学的向量描述，分析力学使用标量表达，基于最小作用量原理，使得力在这一框架中并非必需，而是通过坐标和动量之间的关系自然涌现。 哈密顿正则方程作为拉格朗日方程的推演结果，进一步扩展了分析力学的表述方式，它给出了2s个一阶微分方程，这些方程揭示了系统中潜在的对称性和守恒定律之间的内在联系。即使面对一些实际问题中未知的约束力，如单摆系统中悬垂固定点对摆线施加的力，拉格朗日方程也能通过保守体系的能量守恒原则进行处理，即使这些力是随时变化的。 在处理不同坐标系时，拉格朗日方程也展现出了灵活性。例如，在笛卡尔坐标下，可以通过展开来处理约束方程；而在极坐标系中，径向动力学方程和切向方程分别对应着系统的运动特征。这些方程不仅适用于直线运动，还适用于旋转运动，如科里奥利力和惯性离心力的分析。 当系统处于非惯性系时，如质点在随轴旋转的圆环上，拉格朗日方程能够准确描述在非惯性参考系中的运动，包括惯性力的计算。这种能力使得理论力学能够跨越经典力学的局限，处理更复杂和动态的物理情境。 拉格朗日方程是理论力学的基石之一，它提供了一个强大而通用的工具，使得科学家能够在没有外力全知的情况下，通过解微分方程预测物体的运动轨迹，同时深入理解力与运动之间的本质关系，以及保守性和对称性的物理含义。无论是牛顿力学、相对论力学还是量子力学，都能在拉格朗日方程的框架下找到其位置，展示了分析力学作为“力学的力学”的深远影响力。