清华笔记：离散曲面曲率流的双曲几何与应用

在清华大学的计算共形几何讲义中，第20讲聚焦于离散曲面曲率流（Discrete Surface Ricci Flow）II的内容。本讲义深入探讨了双曲几何在理解离散曲率流解存在性中的关键作用。首先，双曲几何提供了一个重要的数学框架，包括复平面单位圆盘上的黎曼度量，如庞加莱模型，它是双曲平面的标准表示，其中莫比乌斯变换是刚体变换的基本形式。在这个模型中，双曲直线与欧氏圆弧相关联，而双曲圆则与圆心距离保持恒定，尽管圆心位置与欧氏圆不同。 接着，课程介绍了另一种双曲平面模型，其中实数轴代表无穷远直线，测地线为垂直于实数轴的直线或半圆弧。计算两点间的双曲距离需要用到特定的交比方法，对于理想的双曲三角形，其边长无穷大，内角为零但有非零面积，这些特性使得它们在粘贴时形成等距关系。然而，通过瑟斯顿的Shear Coordinates，可以描述这些三角形的粘贴方式，不同坐标下的双曲测地四边形具有不同的等距性。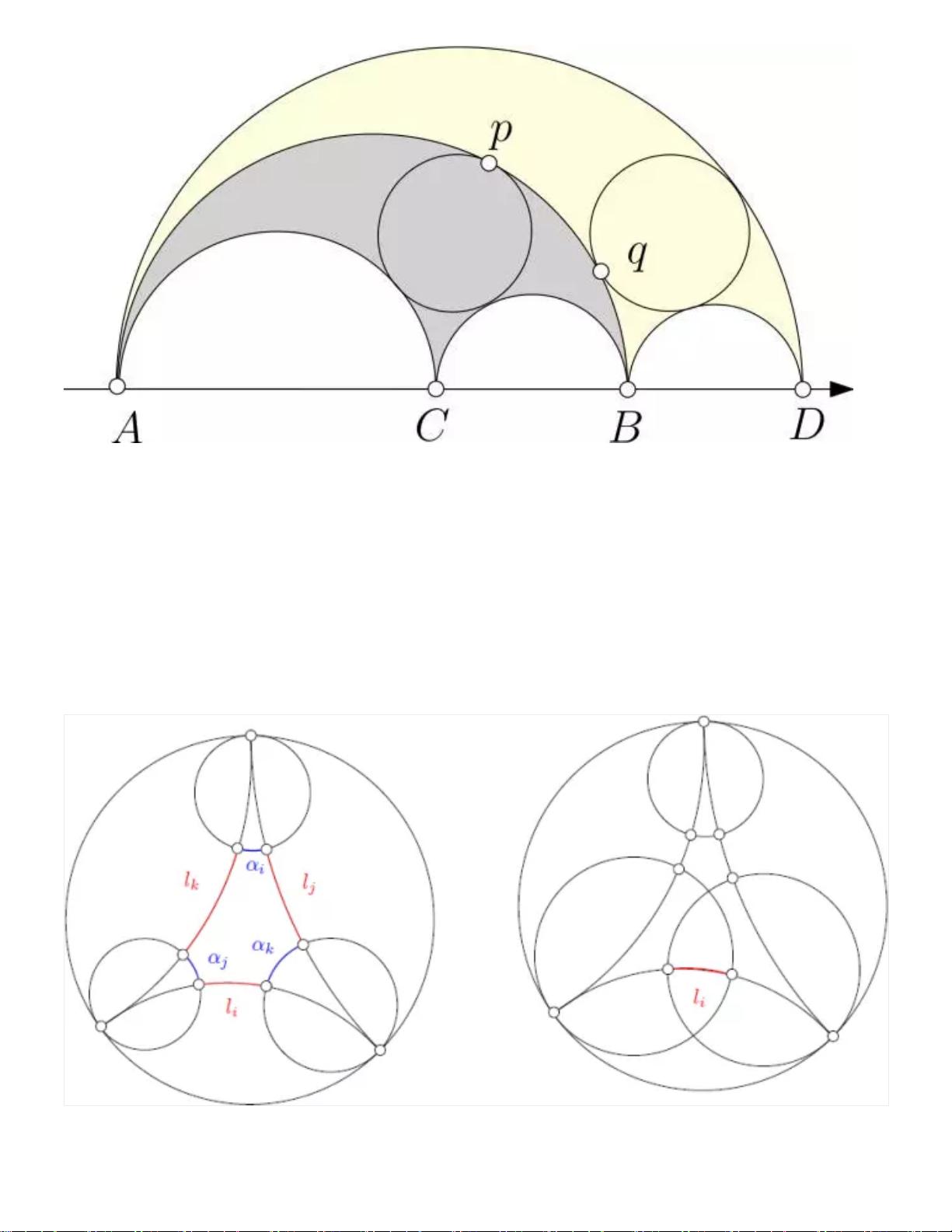 此外，讲义还特别提到了Penner的装饰三角形，这是一种在双曲几何研究中常用的构造，通过装饰三角形，可以进一步分析和处理离散曲面的复杂结构。这些装饰元素在离散曲面的曲率流动过程中扮演着核心角色，它们不仅帮助定义离散化的曲率能量，而且是设计数值算法的基础。 这一部分的内容深入挖掘了双曲几何在离散曲面曲率流中的应用，涉及的关键概念包括双曲空间、黎曼度量、莫比乌斯变换、双曲距离、理想三角形、Shear Coordinates以及装饰三角形，这些都是理解并设计相关算法和技术的关键数学工具。通过学习这些理论，学生能够掌握如何用离散化的双曲几何方法来模拟和优化曲面形状，这对于计算机图形学、几何建模以及相关软件开发等领域具有重要意义。