二叉树重建：基于前序和中序遍历

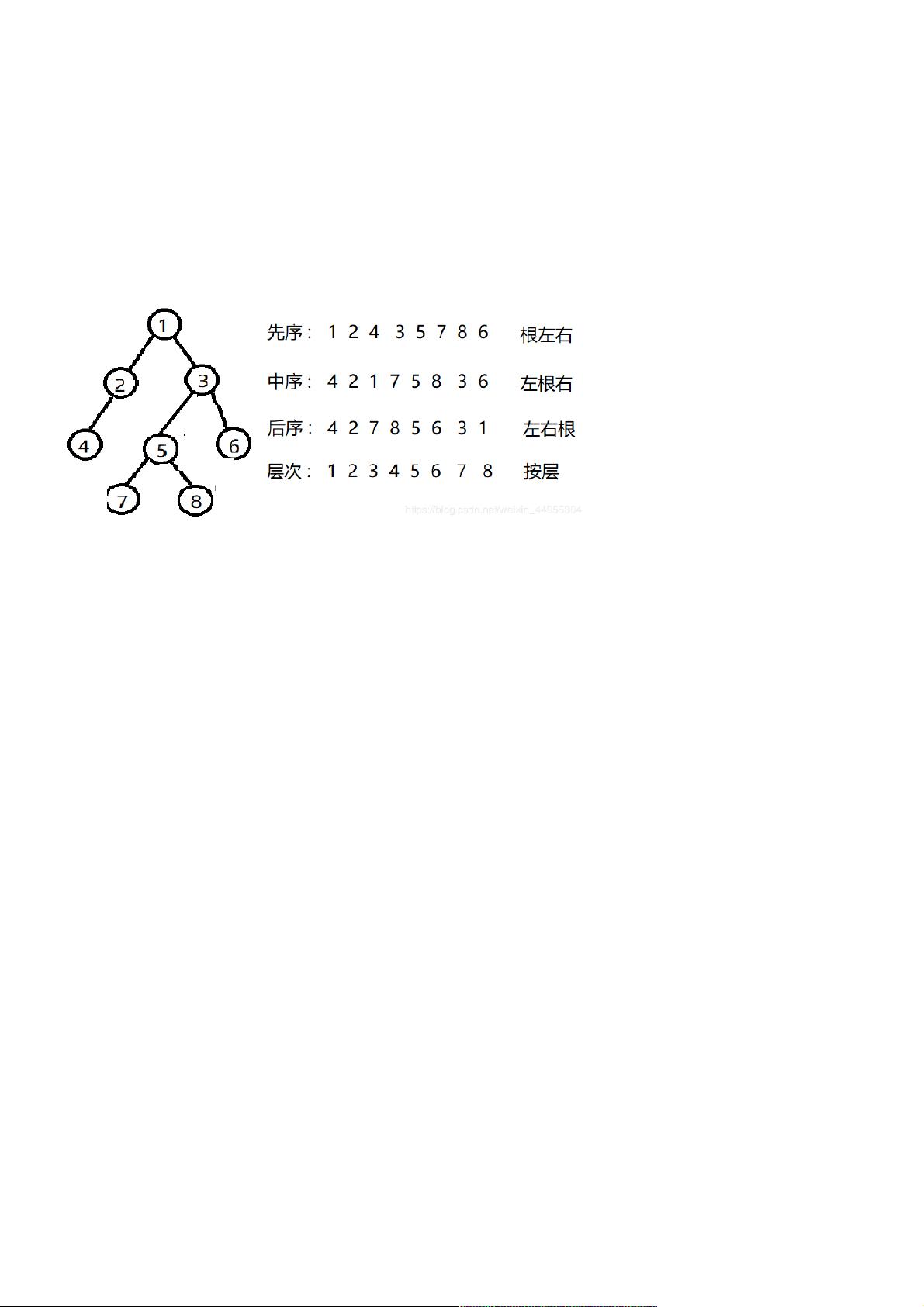
"这篇资源主要讨论了如何根据二叉树的前序遍历和中序遍历结果重建二叉树的问题，并提供了相关的Python代码实现。此外，还介绍了二叉树的基本概念和遍历方法。" 在计算机科学中，二叉树是一种特殊的树结构，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树常用于数据存储、搜索和排序等算法中。重建二叉树的关键在于利用前序遍历和中序遍历的特性来确定每个节点的位置。 前序遍历（Preorder Traversal）的顺序是：根节点 -> 左子树 -> 右子树。中序遍历（Inorder Traversal）的顺序是：左子树 -> 根节点 -> 右子树。通过这两个遍历序列，我们可以找到二叉树的根节点，然后递归地构建左子树和右子树。 重建二叉树的过程如下： 1. 在中序遍历序列中，根节点是唯一的一个值，它的左边是左子树的值，右边是右子树的值。 2. 在前序遍历序列中，根节点是第一个出现的值，之后的值对应左子树，最后的是右子树。 给定前序遍历序列和中序遍历序列，我们可以使用递归的方法来重建二叉树： - 首先，找到前序遍历中的第一个元素，这是根节点的值。 - 在中序遍历序列中找到这个值，它的左侧子序列是左子树的中序遍历，右侧子序列是右子树的中序遍历。 - 使用这两个子序列和对应的前序遍历子序列，递归地构建左子树和右子树。 Python代码实现如下： ```python class TreeNode: def __init__(self, val=None, left=None, right=None): self.val = val self.left = left self.right = right class BinaryTree: def __init__(self, root=None): self.root = root def build_tree(self, preorder, inorder): if not preorder or not inorder: return None root_val = preorder.pop(0) index = inorder.index(root_val) root = TreeNode(root_val) root.left = self.build_tree(preorder, inorder[:index]) root.right = self.build_tree(preorder, inorder[index+1:]) return root ``` 这里定义了一个`TreeNode`类来表示二叉树的节点，以及一个`BinaryTree`类包含了重建二叉树的方法`build_tree`。这个方法首先检查遍历序列是否为空，然后找到根节点的值和其在中序遍历序列中的位置，最后递归地构建左子树和右子树。 除了前序遍历和中序遍历，二叉树还有其他几种遍历方式： - 后序遍历（Postorder Traversal）：左子树 -> 右子树 -> 根节点。 - 层次遍历（Level Order Traversal）：从根节点开始，逐层从左到右访问所有节点。 这些遍历方法各有特点，适用于不同的问题，例如后序遍历常用于计算表达式树，层次遍历常用于解决最短路径问题等。了解和掌握这些遍历方法对于理解和应用二叉树算法至关重要。