最小生成树算法详解：实现与应用

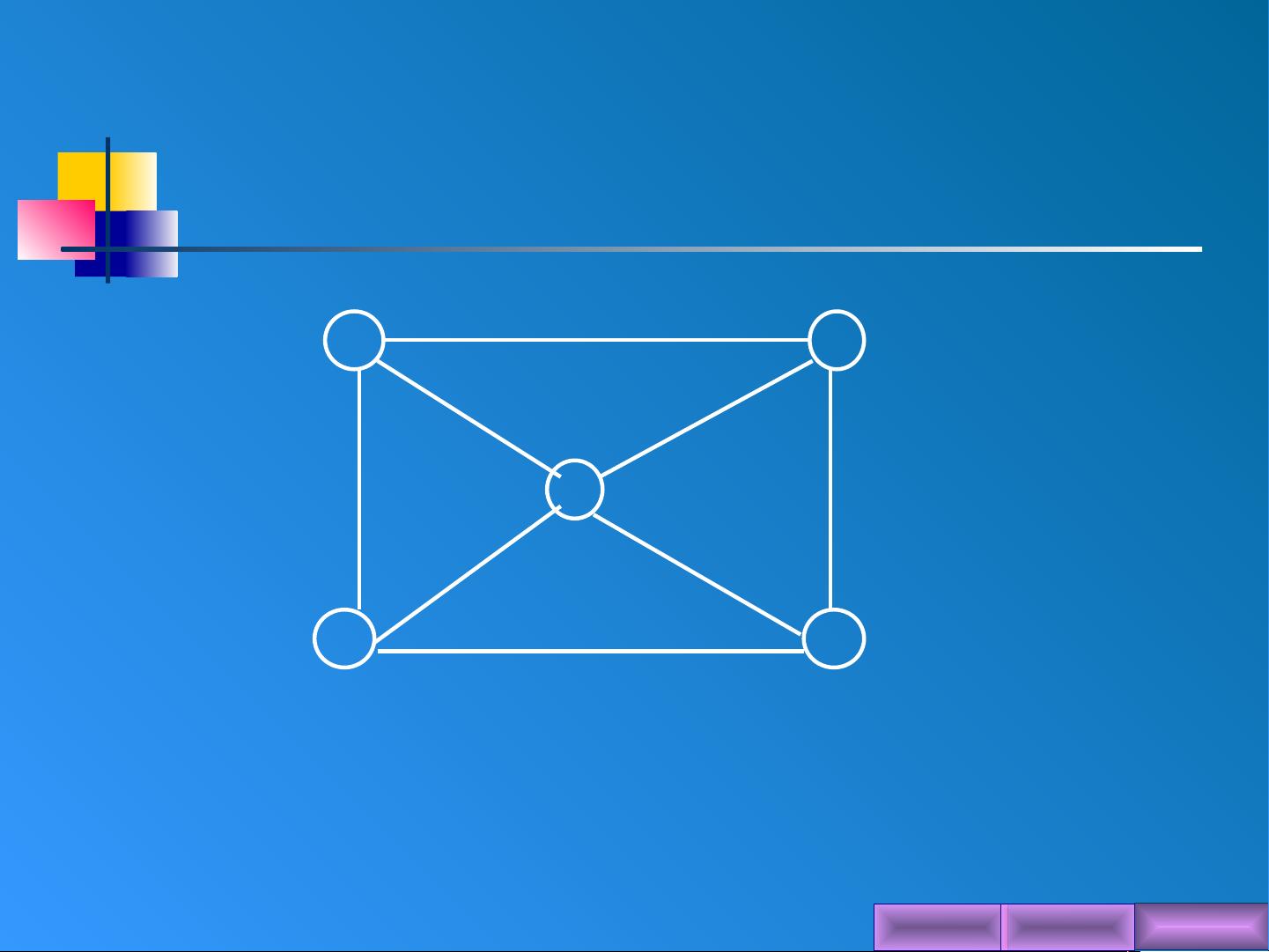
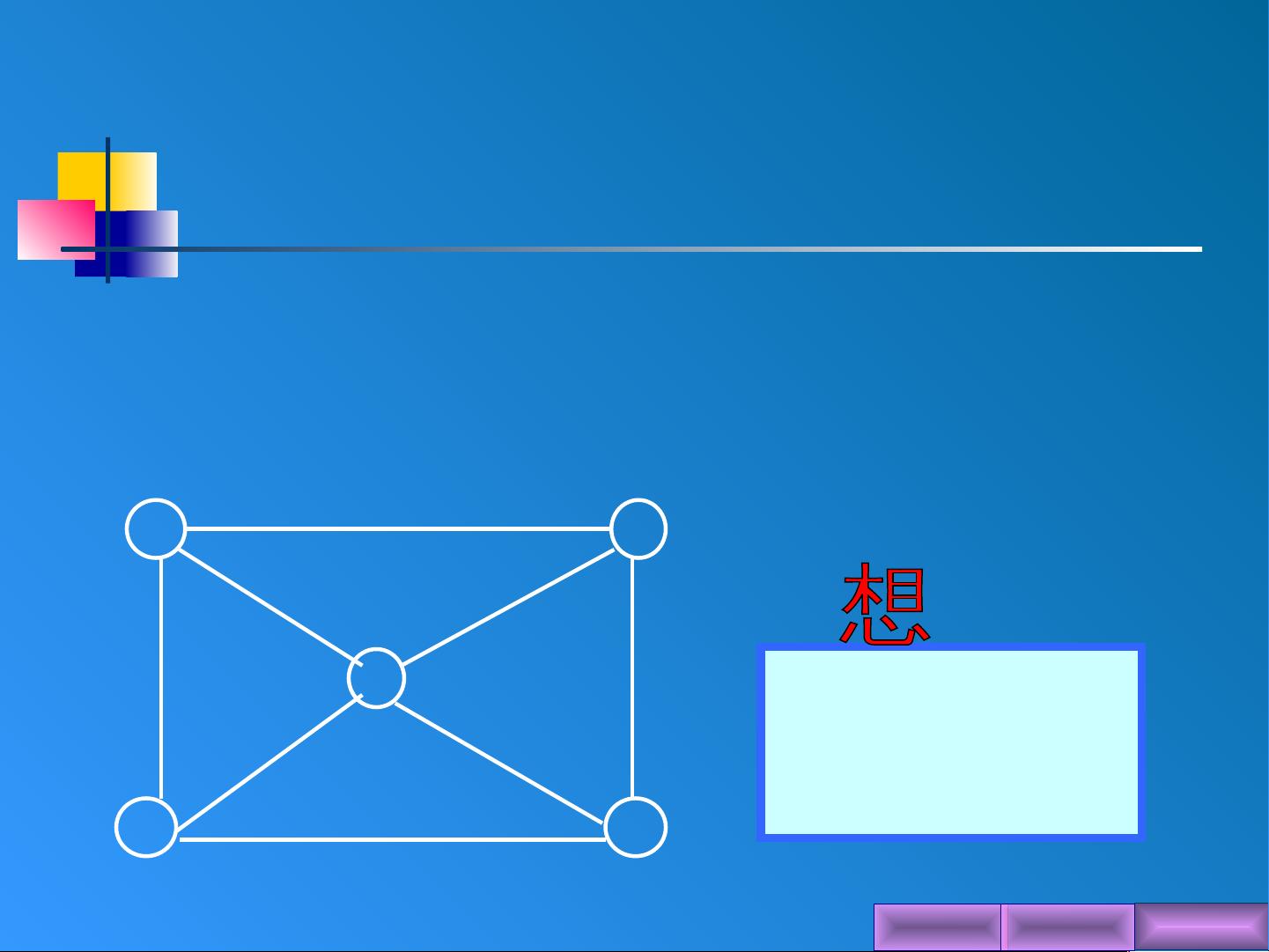
最小生成树是一种在图论中用于寻找无环子图，同时连接所有顶点的方法，它在计算机网络、电信工程、数据分析等领域具有广泛应用。这个话题主要关注两种常见的最小生成树算法：Prim算法和Kruskal算法。 Prim算法，由克鲁斯（Prim）提出，是一种贪心算法，它从一个初始顶点开始，逐步添加边，每次选择当前未加入树的顶点中与已存在树相连且代价最小的边，直到形成一棵覆盖所有顶点的树。这个过程保证了最终生成的树是最小生成树，因为每一步都是选择成本最低的扩展。 Kruskal算法，由库尔萨克（Kruskal）发明，则采用并查集的数据结构来构建树。它首先对所有边按权重排序，然后从小到大依次尝试将边加入树中，只要这条边不形成环就接受，否则就跳过。Kruskal算法同样确保了最终结果为最小生成树。 在实际应用中，如城市电信局规划网络布局时，最小生成树算法可以帮助确定最经济的线路连接方式，以达到最小化建设成本和最大化的通信效率。例如，通过树图的形式，可以直观地展示各个站点之间的关系以及连接路径，使得决策者能够清晰地理解网络拓扑结构。 最小生成树算法的学习通常包括理解基本概念，如树的定义（没有环的连通图，每个节点间有唯一的路径），树的边数与顶点数的关系，以及算法的工作原理和实际操作。同时，学习者还可以参考教材如《数学实验》（傅鹂龚劬刘琼荪何中市编著）和《数据结构教程C语言版》（张绍民李淑华编著）来深入理解和实践这些理论。 MATLAB编程是学习算法的重要工具，通过编写和运行代码，学生可以亲身体验算法的实现过程，从而提高算法理解和解决问题的能力。在课程中，可能会提供一个具体的实例来演示Prim和Kruskal算法如何在一个实际问题中找到最小生成树。 最小生成树算法是网络设计中的核心技术，它不仅涉及基础的图论知识，还强调实际问题的应用和算法的实现技巧。对于初学者来说，掌握这一概念和方法，对于理解和解决许多实际场景下的优化问题至关重要。