多目标规划方法详解：非劣解与求解策略

算法中的多目标规划方法讲义.pptx是一份关于数学模型算法的详细教程，主要聚焦于多目标规划这一领域。多目标规划，简称MOP，是指在优化过程中同时考虑两个或多个目标函数，这些目标可能是相互竞争或不完全协调的。帕雷托最早于1896年研究了此类不可比较目标的优化问题，随后众多数学家如冯·诺伊曼、库恩、塔克和日夫里翁等人进行了深入研究，但至今尚无一个普遍接受的完美定义。 解决多目标规划问题的主要方法包括： 1. 化简方法：如主要目标法、线性加权法和理想点法，将多目标转化为单目标或双目标，使其变得更容易处理。 2. 分层序列法：根据目标的重要性逐次优化，每次在前一个目标的最优解集中寻找下一个目标的最佳解，直到找到共同的最优解。 3. 线性规划的修正单纯形法：针对线性问题，可以对传统单纯形法进行调整。 4. 层次分析法：由沙旦提出，是一种定性和定量结合的决策与分析工具，适用于目标复杂且数据不足的情况。 多目标规划问题的数学模型通常包括两个基本部分： - 目标函数：至少两个，用k维函数向量Z=F(X)表示。 - 约束条件：用若干个m维函数组成的向量(X)和常数向量G来表述，涉及n维决策变量X。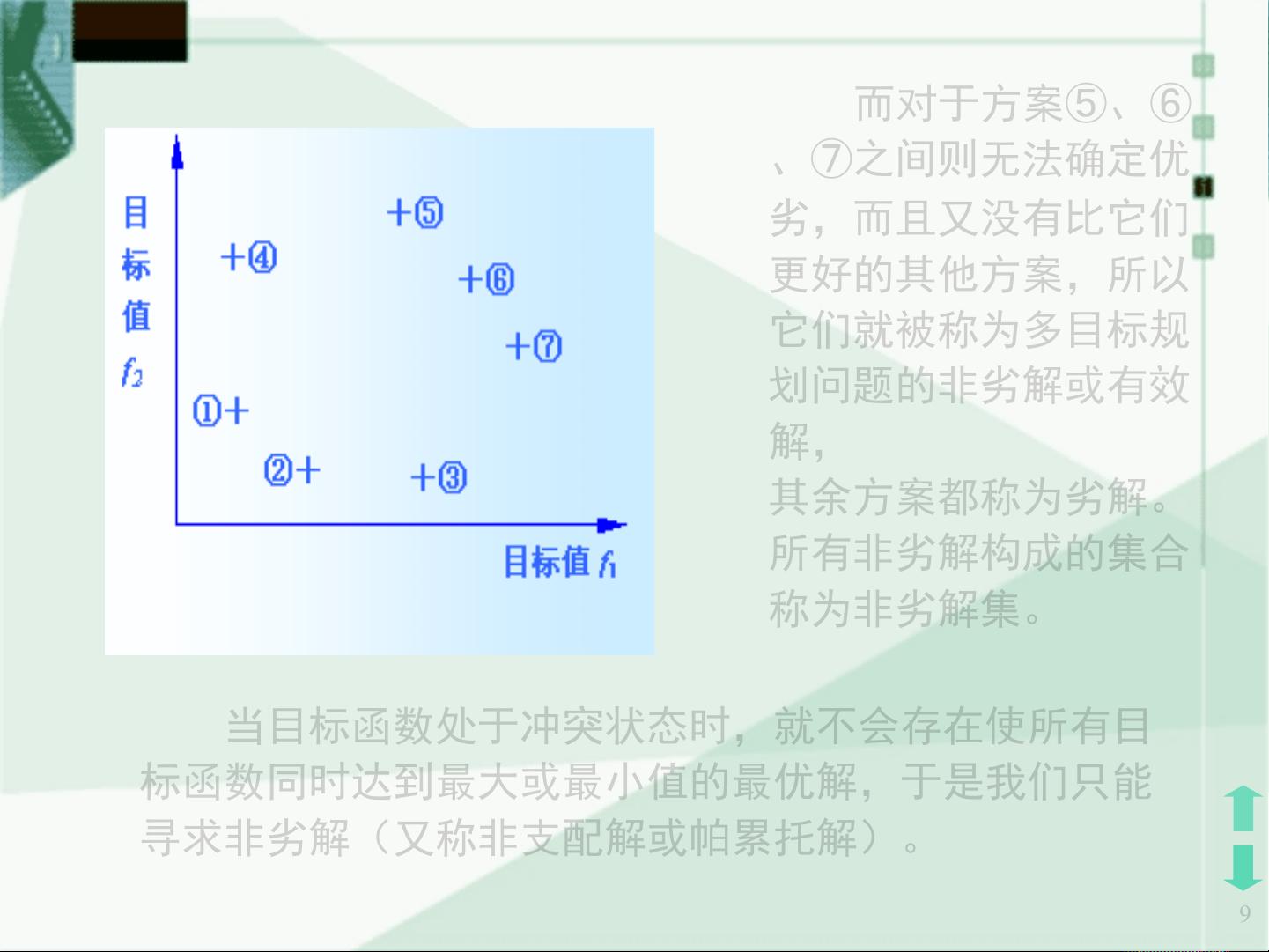 对于线性多目标规划，可以用矩阵形式表示： - 决策变量向量X - 目标函数系数矩阵C - 约束方程系数矩阵B - 约束向量b 在多目标规划中，求解不是寻找单一最优解，而是寻找所谓的"非劣解"，即无法在所有目标中同时达到最优，但每个目标都不逊色于其他解。这意味着决策者需要在目标之间做出折衷，找到一个平衡点，以满足不同目标的需求。 在课程的实例部分，会展示如何应用多目标规划方法解决实际问题，可能涉及经济决策、项目管理、工程设计等领域的复杂决策场景。通过这些实例，学生可以理解多目标规划的实用性以及在不同情境下的应用策略。