MATLAB在电路分析中的应用——复数运算与相量图

"该资源是关于使用MATLAB进行电路分析的教程，重点介绍了在电路分析中常用的复数运算函数，并通过实例演示了如何利用MATLAB解决实际电路问题。" 在电路分析中，MATLAB是一个强大的工具，尤其对于复数运算和相量分析，它提供了丰富的函数来简化计算过程。以下是对这些函数的详细解释： 1. `real(A)`：这个函数用于提取复数或复数矩阵A的实部。在电路分析中，实部通常代表无功分量。 2. `imag(A)`：此函数用于获取复数或复数矩阵A的虚部，虚部对应于电路中的相位差和有功分量。 3. `abs(A)`：计算复数或复数矩阵A的模，即复数的大小或幅度，这在计算电流或电压的大小时非常有用。 4. `conj(A)`：返回复数或复数矩阵A的共轭，这对于处理相量的共轭对称性很重要，例如在计算功率时。 5. `angle(A)`：这个函数返回复数或复数矩阵A的相角，以弧度为单位。在电路分析中，相角表示相位差，对于理解和计算相量关系至关重要。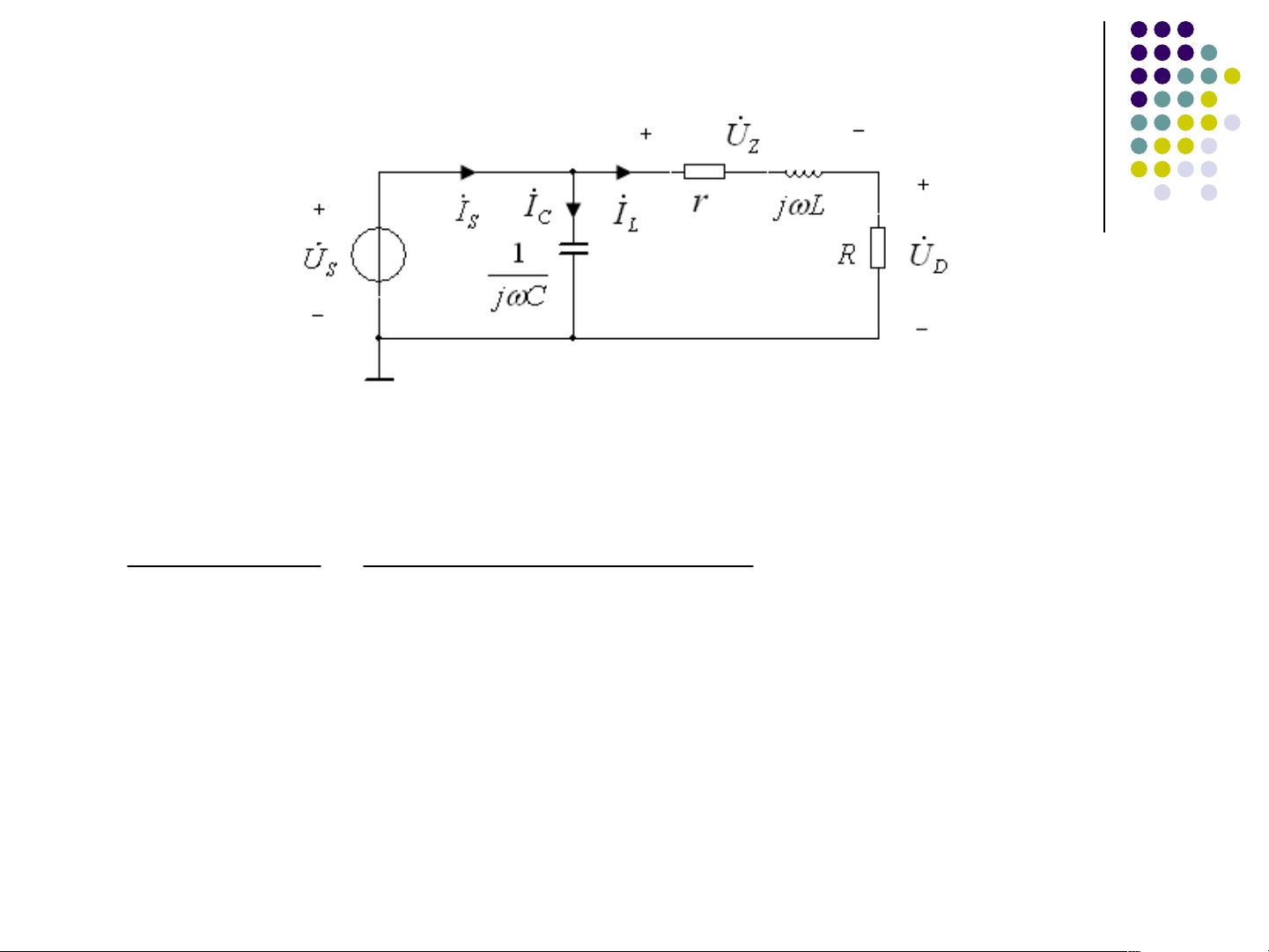 在提供的示例1中，计算了一个包含电阻、电感和电容的电路的电压源的平均功率、无功功率和视在功率。通过使用MATLAB的复数运算函数，可以方便地找到等效阻抗，进而计算电流和复功率。最终，通过`real()`和`imag()`函数分别得到平均功率和无功功率，`abs()`函数则用于计算视在功率。 此外，`compass`函数用于绘制向量图，这是可视化相量关系的重要工具。调用`compass([I1, I2, I3…])`可以绘制由相量构成的向量图，这在分析多相电路或者理解相量之间的相互作用时非常有用。 在示例2中，日光灯电路被等效为一个包含电阻、电感和电容的模型，通过`compass`函数可以绘制出这些元件的相量图，从而分析提高功率因数的效果。 总结来说，MATLAB在电路分析中的应用主要体现在以下几个方面： - 复数运算：通过内置函数处理复数的实部、虚部、模和相角，简化复杂数学计算。 - 相量图绘制：`compass`函数用于直观展示相量关系，帮助理解电路行为。 - 实际问题求解：编写MATLAB程序，能够快速准确地计算电路中的功率、电流和电压等关键参数。 通过掌握这些MATLAB功能，工程师和学生可以更有效地分析和设计各种复杂的电路系统。