PID算法入门与实践指南

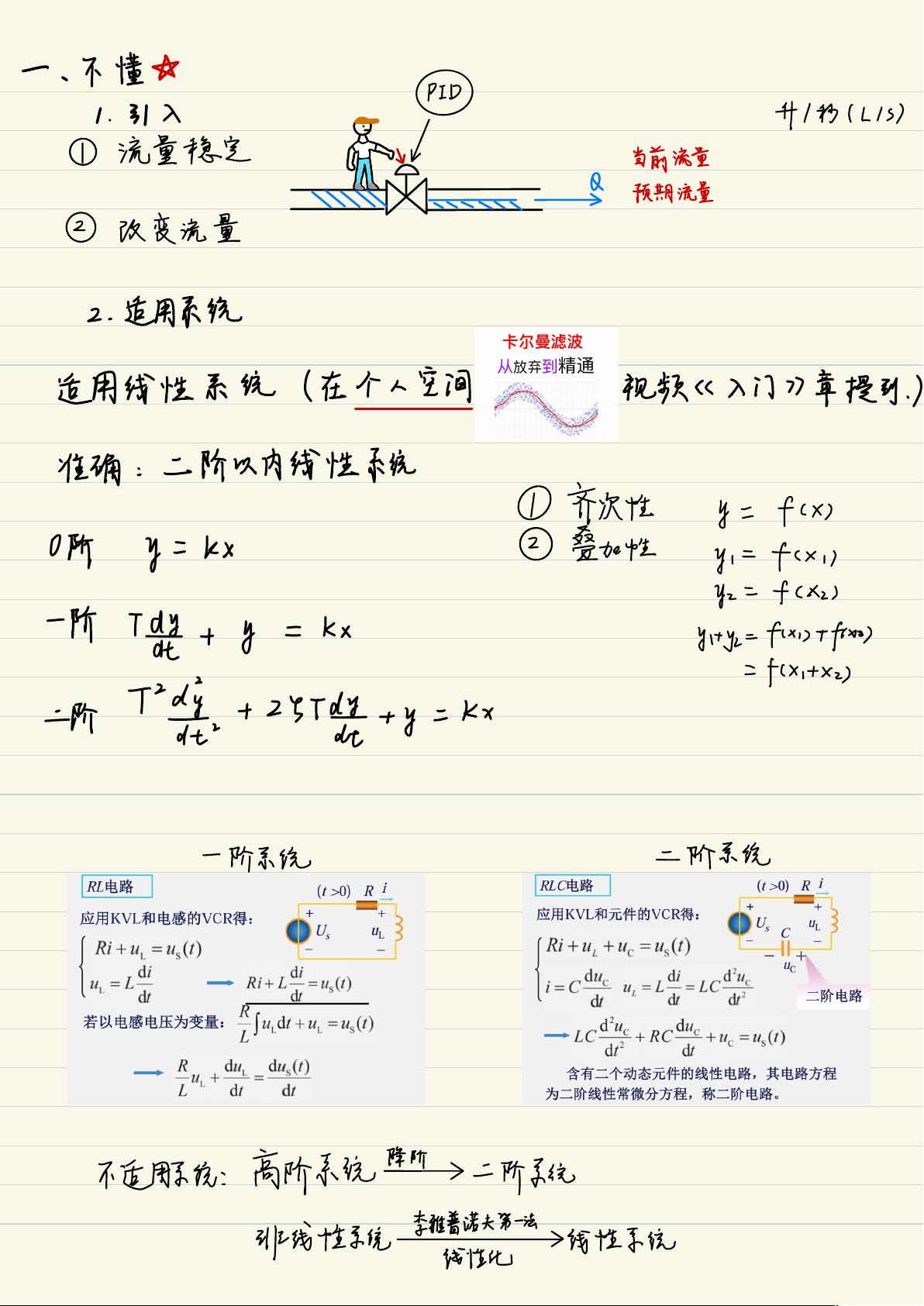
"PID算法Clang.pdf - 一个关于PID算法从入门到实现的教程，主要由华工机器人实验室421施公队编撰。内容涵盖了PID算法的基本概念、适用系统、理论解析以及如何在实际应用中使用PID控制器。" PID（比例-积分-微分）算法是自动控制理论中广泛使用的控制策略，它通过结合比例、积分和微分三个部分来调整系统的响应。本教程的目标是帮助读者从完全不懂到能够熟练应用PID算法。 1. PID算法的引入： PID算法主要用于闭环控制系统，通过调整控制器的三个参数（P、I、D），可以有效地改善系统的稳定性和响应速度。它适用于线性系统，特别是二阶及以下阶次的系统。对于高阶或非线性系统，PID可能不是最佳选择，但其简单易用的特点使其在工程实践中占主导地位。 2. 控制系统概述： - 开环控制系统：不包含反馈机制，输出仅取决于输入，不受系统状态影响。 - 闭环控制系统：包含反馈机制，能够根据实际输出与期望输出的偏差进行自我调整。 - 双闭环控制系统：在单闭环基础上增加另一个回路，通常用于更复杂系统的控制，如速度和位置的双重控制。 - 前馈控制和复合控制系统：前馈控制基于已知干扰来补偿，而复合控制结合了前馈和反馈控制的优点，提高系统的鲁棒性。 3. PID的基本组成部分： - 比例（P）项：立即响应误差，提供快速响应。 - 积分（I）项：消除稳态误差，通过积累过去的误差来调整控制。 - 微分（D）项：预测未来的误差趋势，提供超前控制，减少系统振荡。 4. 连续与离散信号： 在实际应用中，PID算法既可以用于连续时间系统（连续信号），也可以用于离散时间系统（数字信号）。离散PID控制常在数字电子设备中使用，通过采样时间和计算方法调整，以模拟连续系统的控制效果。 5. PID参数整定： 参数整定是PID控制器设计的关键步骤，包括手动试凑、经验法则、临界比例度法、响应曲线法等多种方法。每种方法都有其优缺点，需要根据具体系统特性进行选择。 总结，本教程旨在帮助读者理解PID算法的基础原理，掌握其在不同系统中的应用，并学会如何对PID控制器的参数进行有效整定，以实现系统的优化控制。通过学习，读者将具备在实际项目中运用PID算法的能力。