人脸识别中的坐标变换与欧拉角计算

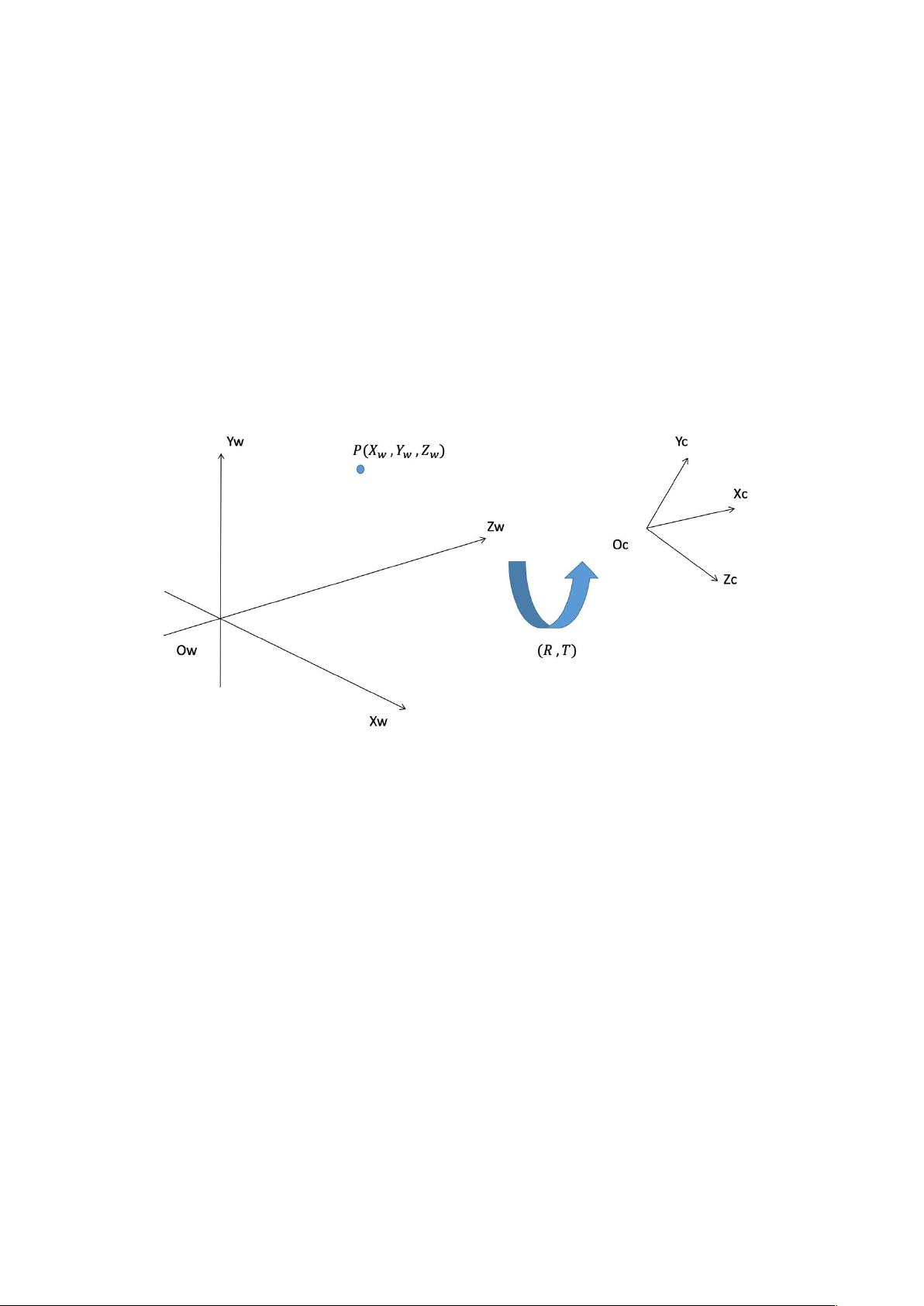
"本文介绍了人脸识别中涉及的坐标变换和欧拉角计算方法，包括从世界坐标系到像素坐标系的三次坐标变换过程，以及如何求解旋转矩阵和位移矩阵。" 在人脸识别技术中，理解并处理不同坐标系之间的转换至关重要。这种转换涉及到四个主要的坐标系：世界坐标系（Ow-XwYwZw）、相机坐标系、像面坐标系和像素坐标系。这些变换用于将真实世界中的人脸位置准确地映射到图像的像素位置上。 首先，从世界坐标系到相机坐标系的变换涉及到旋转和位移。旋转矩阵R由三个基本旋转矩阵R1、R2和R3组成，分别对应于绕Z、X和Y轴的旋转。通过罗德里格矩阵模型，我们可以计算出这些旋转矩阵，然后组合成完整的旋转矩阵。位移矩阵T则表示物体在空间中的平移。最终的变换矩阵为R和T的组合，它描述了从世界坐标系到相机坐标系的完整变换。 接着，从相机坐标系到像面坐标系的转换考虑了焦距f的影响。通过焦点对称原理，可以推导出相机坐标到像面坐标的变换矩阵，这个矩阵描述了光线通过镜头后在像面上的位置。 随后，从像面坐标系到像素坐标系的变换则考虑了像素尺寸和焦距的关系。每个像素的物理尺寸和像面到传感器的距离会影响最终的像素坐标。 在整个过程中，还有一个尺度因子K，它通常与相机的内在属性相关。在求解旋转矩阵和位移矩阵时，如果已知相机内参，可以忽略K的影响，直接处理从世界坐标系到相机坐标系的变换。 欧拉角是描述三维旋转的一种方式，它由三个角度组成，分别对应于绕不同轴的旋转。在人脸识别中，欧拉角常用于描述人脸的倾斜、俯仰和翻转。通过旋转矩阵，我们可以计算出这些欧拉角，从而更好地理解人脸在图像中的姿态。 这个过程涉及到复杂的数学运算，包括线性代数和几何变换。正确执行这些步骤对于实现精确的人脸识别和追踪至关重要。理解这些概念不仅有助于开发更高效的人脸识别算法，还能为其他计算机视觉应用提供基础，例如目标检测和跟踪。