图论算法详解：遍历与最小生成树

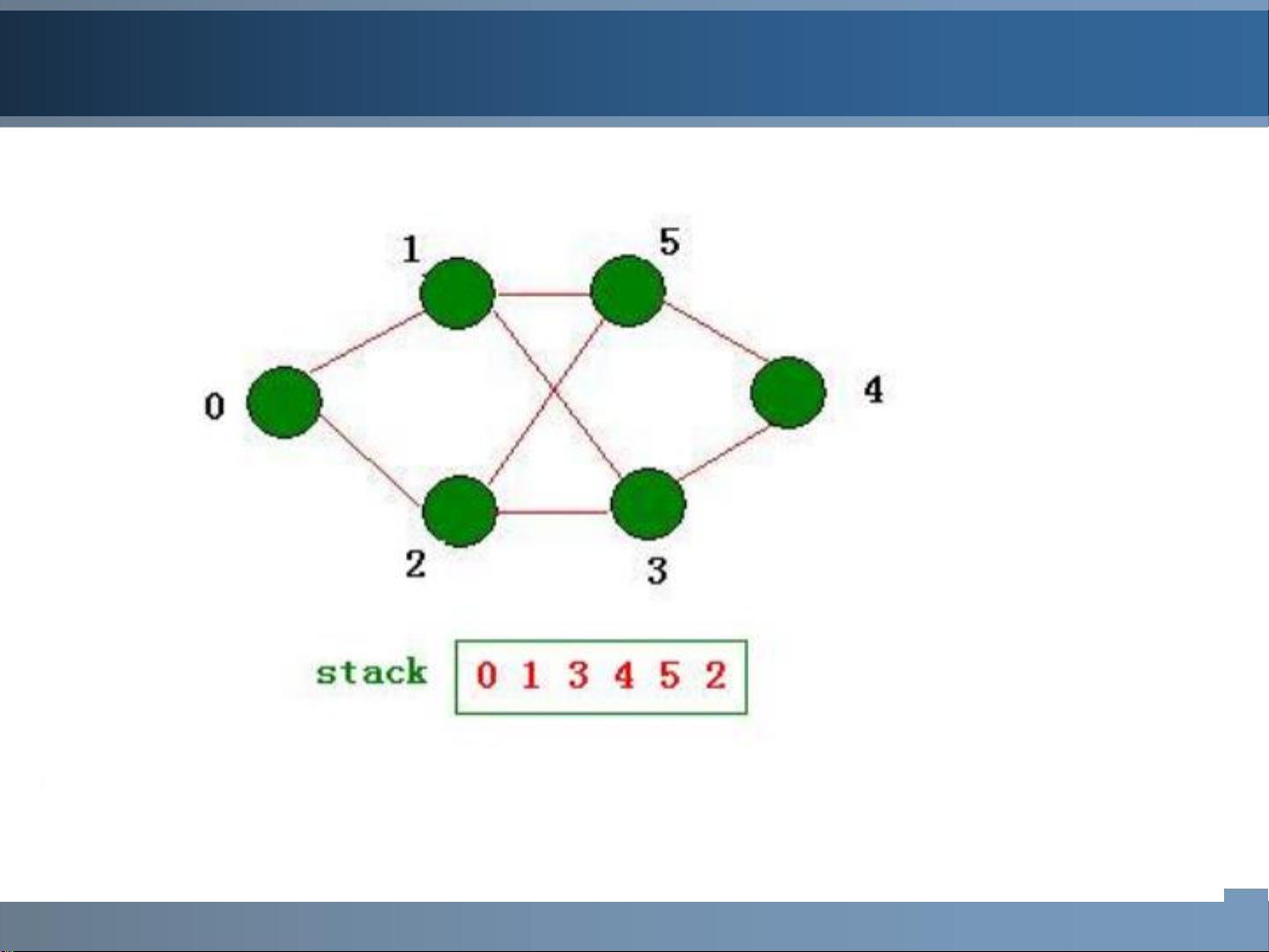
“5-图论算法1（50页）.pdf”主要探讨了图论中的算法，包括图的遍历、最小生成树以及最短路径等问题，适合ACM/ICPC程序设计竞赛和算法学习。 图论算法在计算机科学中扮演着重要角色，特别是在解决复杂网络问题时。本文档首先介绍了图的两种基本遍历方法——宽度优先搜索（BFS）和深度优先搜索（DFS）。这两种方法都是用于遍历或搜索图中的所有节点，确保每个节点只被访问一次。 BFS是一种层次优先的搜索策略，从起始节点开始，逐层访问相邻节点。它使用队列数据结构来存储待访问的节点，每次从队首取出一个节点，然后将其未访问的邻居节点加入队列。BFS在寻找最短路径（在无权图中）和宽度最宽的路径等方面非常有效，其时间复杂度通常为O(V+E)，其中V是节点数量，E是边的数量。 DFS则是一种递归策略，从起始节点开始，沿着一条路径深入探索，直到达到叶子节点或回溯到已访问过的节点。DFS通常使用栈来存储待处理的节点。与BFS不同，DFS更侧重于深度的探索，可以用于检测图中的环路。DFS的时间复杂度同样为O(V+E)。 文档还涉及了最小生成树的构建，这是图论中的一个重要概念。最小生成树是一棵树形结构，包含了原图的所有节点，并且边的权重之和尽可能小。 Prim算法和Kruskal算法是两种常见的贪婪算法，用于构建最小生成树。 Prim算法从一个初始节点开始，逐步添加边，每次都选择当前未加入树中且连接两个不同集合的边中权重最小的一条，直到所有节点都被包含。而Kruskal算法则是按边的权重排序，从最小边开始尝试添加，但避免形成环路，直到连接所有节点。 此外，文档还涵盖了最短路径算法，如Bellman-Ford、Dijkstra和Floyd-Warshall。Bellman-Ford适用于存在负权边的情况，通过松弛操作逐步更新节点间的最短路径。Dijkstra算法适用于无负权边的图，使用优先队列来快速找到源节点到其他节点的最短路径。Floyd-Warshall算法则解决了所有节点对之间的最短路径问题，通过动态规划的方法填充距离矩阵。 最后，文档提供了各种练习题，帮助读者巩固和实践这些图论算法，包括BFS、DFS、Prim、Kruskal、Bellman-Ford、Dijkstra和Floyd-Warshall的练习题目，这有助于提升实际编程和解决问题的能力。