理解算法复杂度：从概念到分析方法

"关于算法复杂度的概念的PPT" 算法复杂度是衡量算法效率的重要指标，它关注的是在处理问题规模增大时，算法所需的计算时间和内存空间如何增长。本PPT详细介绍了算法复杂度的基本概念及其分析方法。 首先，算法复杂度主要关注问题规模n的增长对算法性能的影响。在分析时，我们通常忽略与问题规模无关的固定计算量和硬件因素，以聚焦于算法的本质性能特征。例如，线性复杂度表示算法时间或空间需求与问题规模成正比，而指数复杂度则表示随着问题规模的增加，需求呈指数级增长。 描述增长趋势时，我们常用简化表达，比如将常数C和线性项f(n)省略，只保留最重要的增长因子，如n或n的更高次幂。例如，f(n)=nk+c可简化为f(n)=nk，而C和c这类与n无关的常数通常被忽略，以突出核心的增长趋势。 在考察算法复杂度时，我们关注三个关键场景：最好情况、平均情况和最坏情况。最坏情况往往最为重要，因为它给出了算法性能的上限保证。例如，对于排序算法，最坏情况通常是输入数据完全逆序，此时算法的运行时间可以用来评估其效率。 大O表示法是描述算法复杂度上界的常见工具，用以表示算法运行时间或空间需求的最大可能增长速度。比如，如果一个算法的时间复杂度是O(n^2)，这意味着随着n的增长，算法的执行时间最多会以n的平方的速度增长。 大Θ表示法则更为精确，它不仅给出了上界，还提供了下界。如果存在两个函数g(n)和f(n)，使得g(n)≤f(n)≤O(g(n))，且g(n)和f(n)在n趋向无穷大时保持相同的增长率，那么我们可以表示算法复杂度为Θ(f(n))。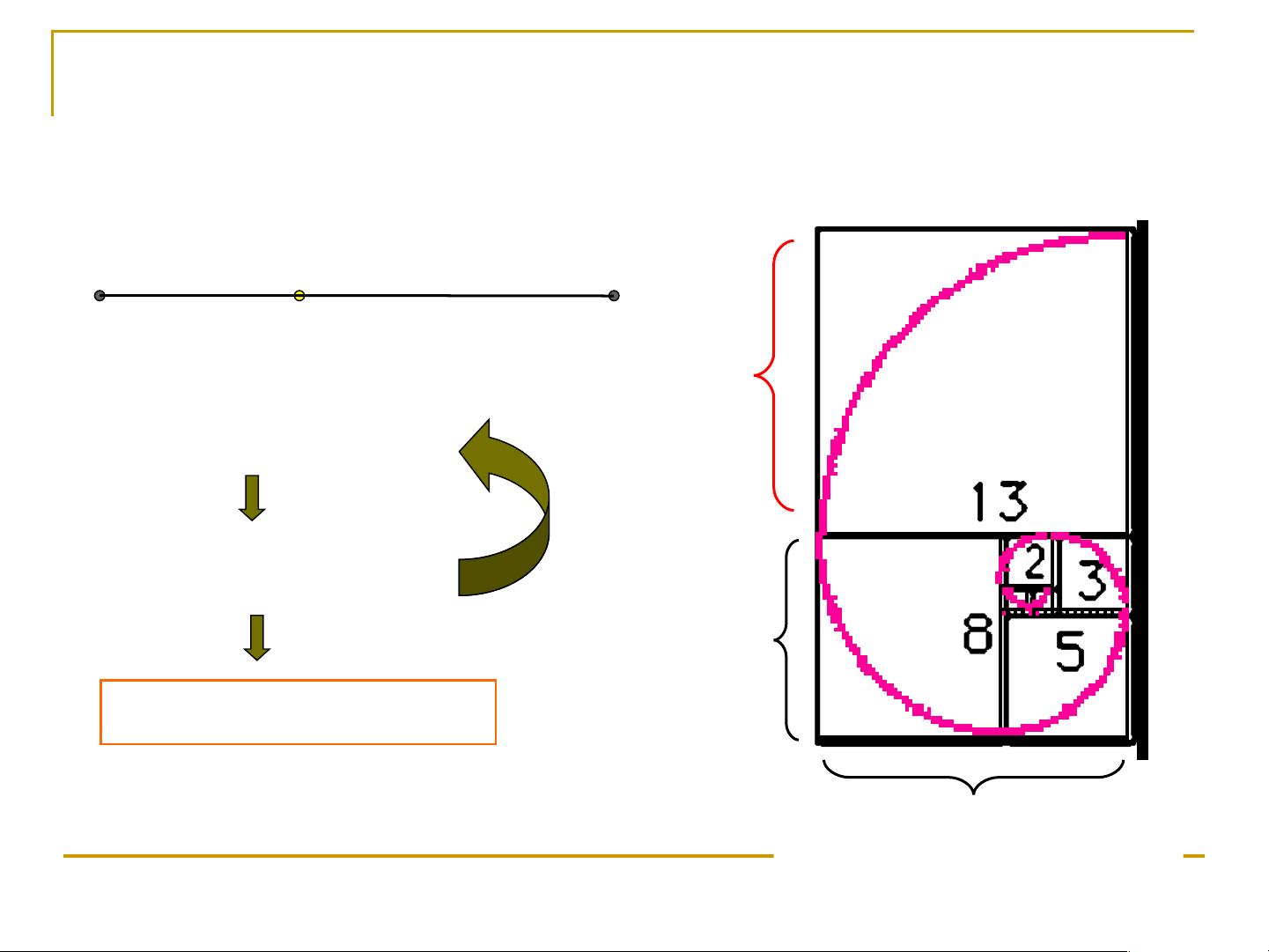 PPT中还通过斐波那契数列问题展示了算法复杂度的优化。斐波那契数列的递归解法会导致大量的重复计算，其时间复杂度为O(2^n)，这是非常高的。然而，通过展开递推公式或者使用动态规划，可以将时间复杂度降低到O(n)，显著提高了算法效率。 理解并分析算法复杂度对于优化算法和设计高效解决方案至关重要。在实际编程中，我们应当尽量追求低复杂度的算法，以确保程序在处理大规模数据时仍然能够快速有效地运行。