SPSS主成分分析步骤详解及结果解读

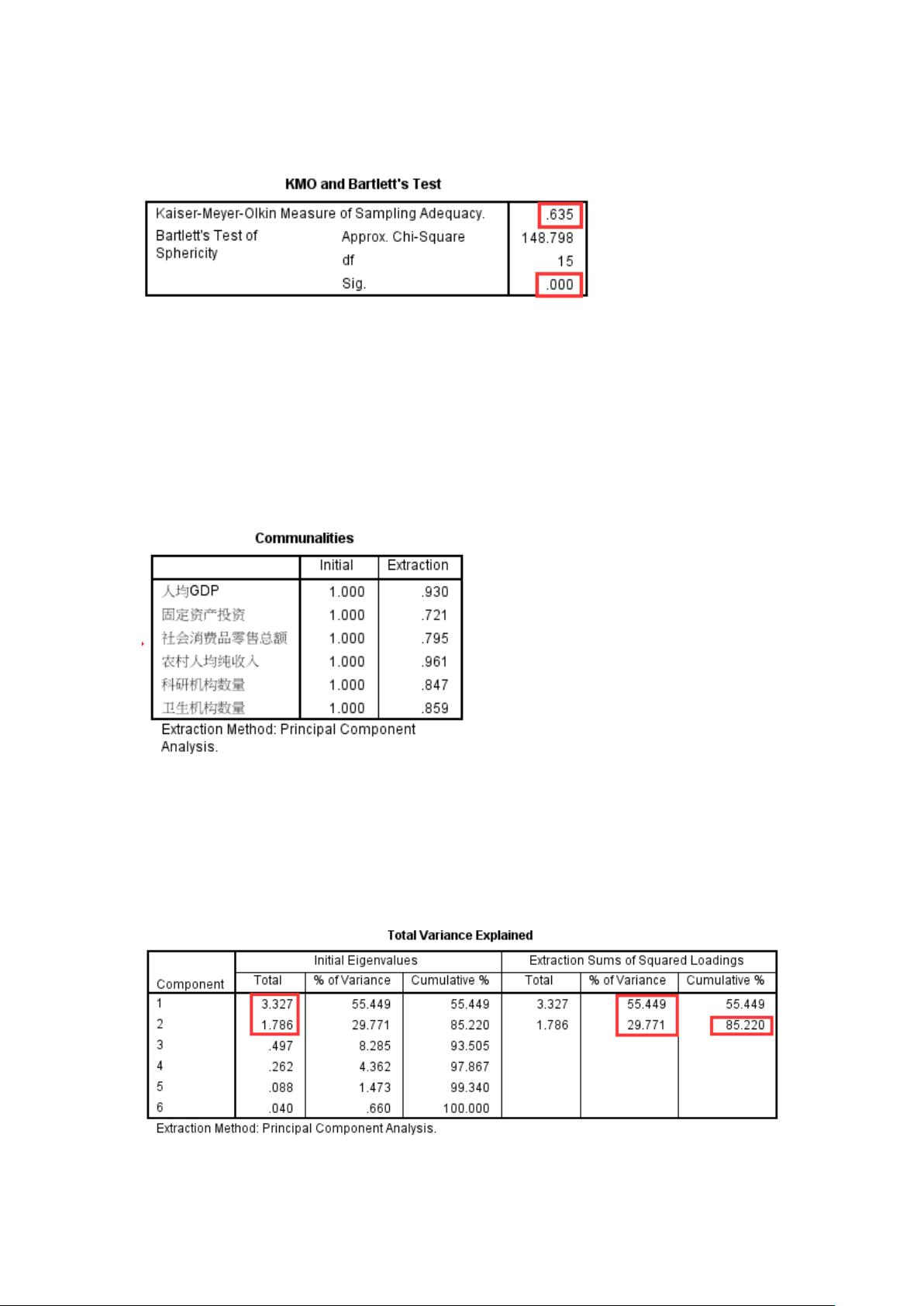
"这篇文档介绍了如何使用SPSS进行主成分分析的步骤，包括KMO和Bartlett球形检验、公因子方差表、总方差分解表、因子截荷矩阵以及如何计算主成分的表达式。" 在统计分析中，主成分分析是一种常用的数据降维方法，它通过线性组合原始变量来创建新的、不相关的变量，这些新变量被称为主成分。这些主成分是原始变量的线性组合，目的是最大化方差并捕获大部分数据的信息。SPSS软件提供了一个用户友好的界面来执行主成分分析。 1. **KMO和Bartlett球形检验**： 在进行主成分分析前，通常需要进行KMO（ Kaiser-Meyer-Olkin Measure of Sampling Adequacy）和Bartlett球形检验。KMO值如果接近1，则表示变量之间存在足够的多重共线性，适合进行因子分析。在这里，KMO值为0.635，大于0.6，说明数据适合进行因子分析。Bartlett球形检验的P值小于0.05，也表明变量之间存在足够的相关性，适合进行分析。 2. **公因子方差表**： 公因子方差表显示了每个变量的共同度，即每个变量与所有变量的平均相关性。若共同度大于0.5，说明主成分对原始变量有较好的解释能力。在这个例子中，各个共同度的值均大于0.5，意味着提取的主成分对原始变量的解释力较强。 3. **总方差分解表**： 这个表格列出了每个主成分的特征值和方差贡献率。通常，特征值大于1的主成分被认为是有意义的。在这个案例中，有两个主成分，它们的特征值分别为3.327和1.786，对应的方差贡献率分别是55.449%和29.771%，累积方差贡献率为85.220%，这表明这两个主成分能够解释数据85.22%的变异。 4. **因子截荷矩阵**： 因子截荷矩阵显示了每个原始变量与主成分之间的相关性，也就是主成分载荷。高载荷值表示该变量对相应主成分的贡献大。通过这个矩阵，可以确定哪些原始变量对每个主成分的影响最大。 5. **计算主成分**： 主成分的计算涉及将因子载荷矩阵与原始数据相乘。在SPSS中，可以创建新变量来表示主成分。例如，通过因子截荷矩阵中的载荷值，我们可以计算出主成分Y1和Y2的表达式，如：Y1 = 0.456X1 + 0.401X2 + ...，Y2 = -0.367X1 + 0.322X2 + ...，其中X1到X6是原始变量。 SPSS提供的主成分分析功能使得研究者能够方便地对复杂数据进行降维处理，理解数据的主要结构，并可能识别出关键的变量或模式。通过执行上述步骤，可以有效地进行主成分分析并解释分析结果。