相平面法分析非线性系统：理论与应用

"本资源为第7章关于相平面法的PPT，主要介绍如何使用相平面法分析非线性系统的响应性能。相平面法是一种分析工具，特别适用于二阶或一阶系统的研究，通过相变量（即状态变量）来描述系统动态。状态变量是表征系统运动状态的关键，它们可以有多组不同的选择。相平面法通过绘制相轨迹来揭示系统的输出响应特性，从而评估超调量、延迟时间等关键性能指标。此外，还介绍了如何将二阶系统的常微分方程转化为相平面形式，并讨论了线性系统相轨迹的特性，特别是由特征方程根的分布决定的自由运动性质。" 相平面法是分析非线性控制系统的一种有效技术，尤其适用于一阶和二阶系统。这里的“相”指的是相变量，它们是一组特定的状态变量，这些变量的数量是最小的，足以完全描述系统的动态行为。状态变量的选择并非唯一，例如在二阶线性控制系统中，输出y(t)和控制器输出c(t)可以是一组状态变量，而误差e(t)和输出y(t)也可以构成另一组状态变量。关键在于，这些变量间的关系应满足导数关系。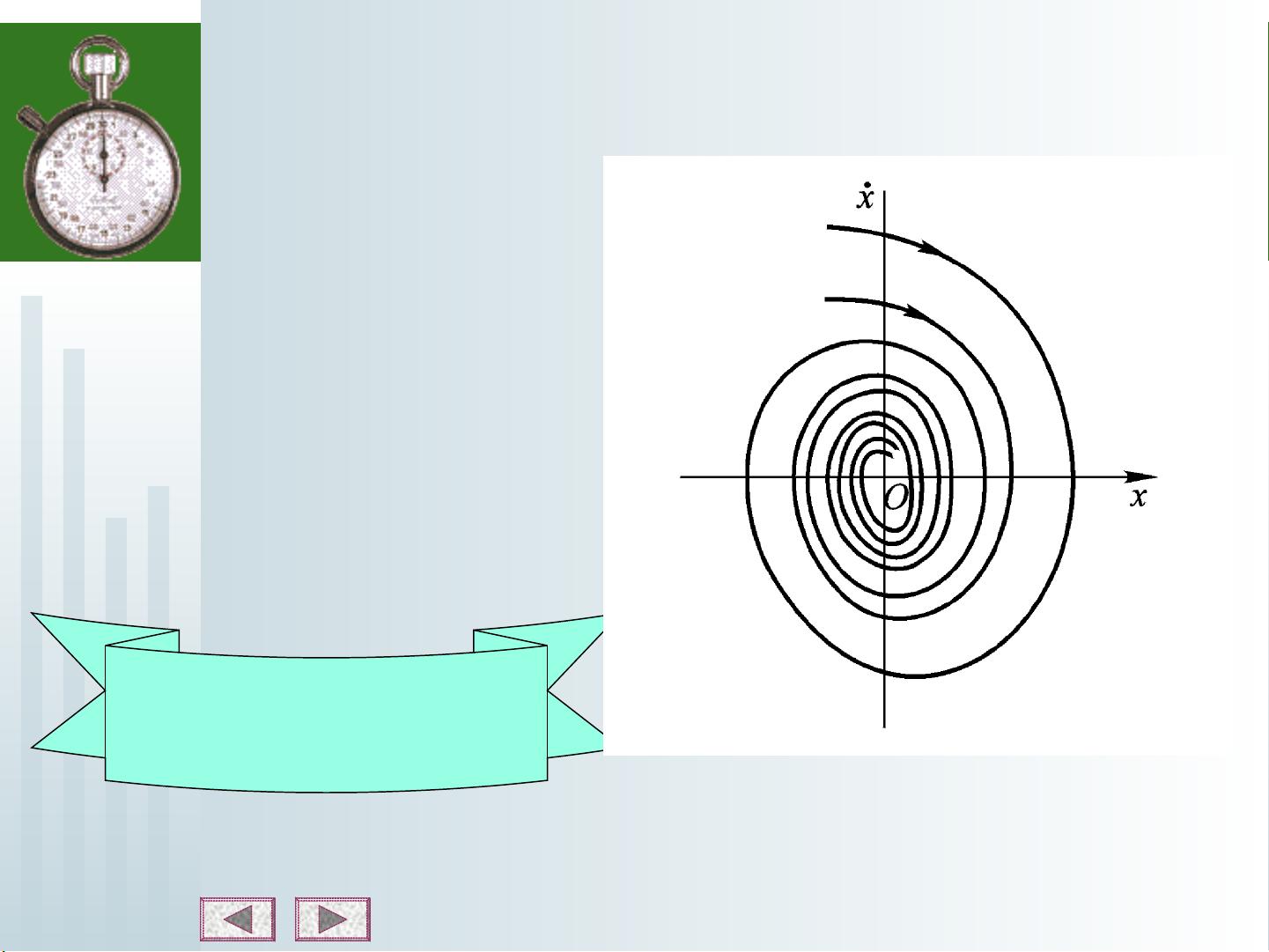 相平面是通过将这些状态变量绘制在二维坐标系中形成的，其中每个轴代表一个状态变量。相轨迹是系统动态行为的图形表示，它是在相平面上随时间演变的曲线。通过观察相轨迹，我们可以分析系统的响应性能，如最大超调量、延迟时间、上升时间、峰值时间和调节时间等关键指标。 例如，对于一个二阶系统，可以通过将输出响应和其导数曲线绘制在同一平面上得到相轨迹。相轨迹的切线斜率对应于该点处的导数值，这有助于我们理解系统的瞬态行为。通常，二阶系统常微分方程可以通过适当的变量变换转化为相平面的形式，然后通过积分找到相轨迹的表达式。 对于线性系统，相轨迹的形状和性质由系统的特征方程决定。特征方程的根决定了系统的自由运动特性，比如稳定的平衡点、振荡行为或者不稳定的行为。根据特征根的实部和虚部，可以推断出相轨迹在相平面上的分布，进一步分析系统的稳定性、振荡模式以及响应速度等特征。 相平面法提供了一种直观且实用的方法来理解和分析非线性系统的动态特性。通过相轨迹的绘制，工程师可以深入洞察系统的动态响应，优化控制策略，以达到理想的控制效果。这种方法对于工程问题的解决和理论研究都具有重要的价值。