信号与系统第二章：连续时间系统中的基本信号及其表示方法

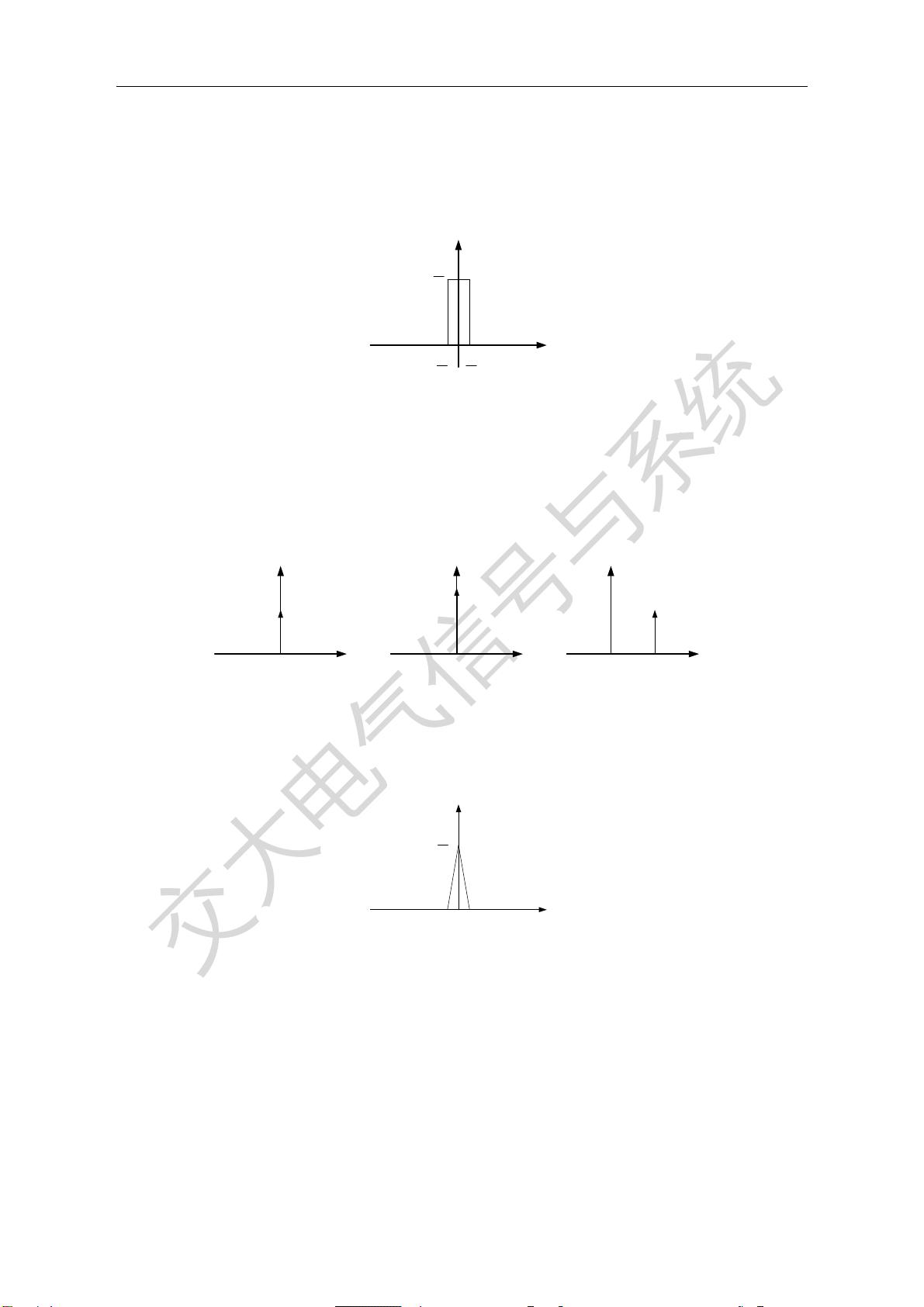
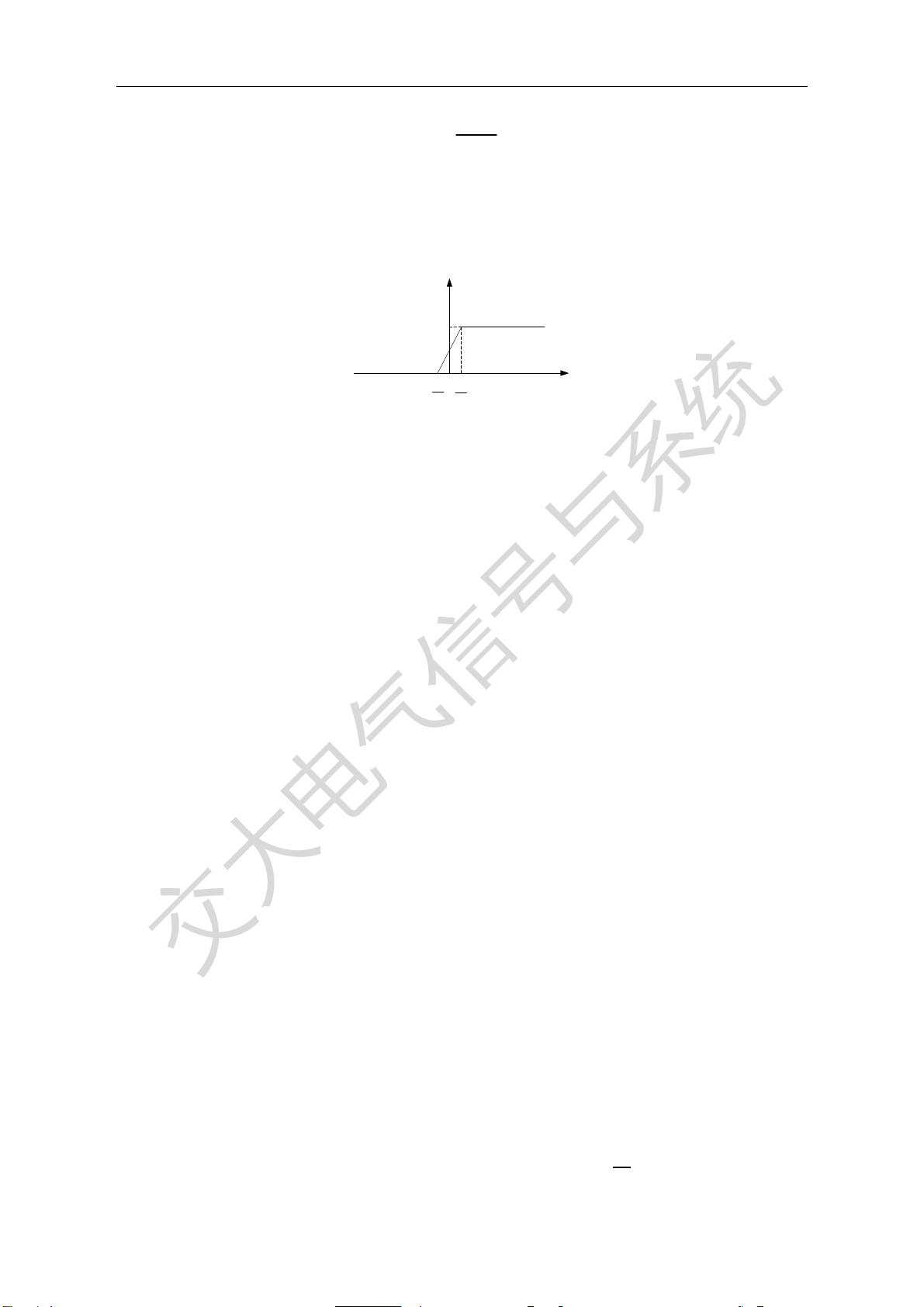
《信号与系统》电子教材的第二章主要介绍了连续时间系统的时域分析。在信号处理中，我们经常需要用数学函数表示信号，但对于实际信号而言，其数学函数表示可能非常复杂。然而，一个信号一般也可以用特定形式信号的线性组合表示，其中包括正弦信号、复指数信号、阶跃信号和冲激信号等。这些特定形式的信号被称为基本信号。 当涉及到线性时不变（LTI）系统时，我们可以利用基本信号来表示系统的输入，并通过系统对基本信号的响应来求解系统的响应。这是因为，利用线性性质和时不变性，我们可以用基本信号的线性组合表示任意信号。而通过系统对基本信号的响应求解，我们可以获得系统的冲激响应，从而揭示系统的性质。因此，除了使用微分方程描述LTI系统外，我们也可以使用冲激响应来描述系统。 在第二章的2.1节中，重点介绍了基本信号的概念。在信号分析中，复杂确定信号通常可以用某种基本信号的组合表示。常用的基本信号包括正弦信号、复指数信号、阶跃信号和冲激信号。正弦信号和复指数信号的导数是连续函数，因此被称为普通信号；而阶跃信号和冲激信号本身是非连续的，它们没有连续函数范畴的导数概念，因此被称为奇异信号。 正弦信号在信号处理中具有重要的地位，因为它可以表示周期性信号，同时也可以通过傅里叶级数展开表示非周期信号。复指数信号是由正弦和余弦信号构成的，它在频域中具有明确的频率和相位信息，因此在频域分析和滤波等应用中很常见。阶跃信号和冲激信号在系统分析中经常使用，它们具有特殊的性质，可以用来描述系统的初始条件和特定事件的响应。 连续时间系统的卷积法分析是本章的重点内容。卷积是一种数学运算，用来描述两个函数之间的关系。在连续时间系统中，我们可以用冲激信号表示任意输入信号，并通过系统对冲激信号的响应（即冲激响应）来求解系统的输出。由于冲激信号的线性组合可以表示任意信号，所以通过冲激响应的求解可以得到系统的输出，从而揭示了系统的性质。 总之，第二章主要介绍了连续时间系统的时域分析。通过基本信号的线性组合表示任意信号，并利用连续时间系统的线性性质和时不变性，我们可以推导出系统的响应。同时，通过卷积法分析，我们可以用冲激响应来描述系统的性质。这一章的内容对于理解和应用信号与系统的基本原理有着重要的作用。