MATLAB模拟理想采样信号序列分析

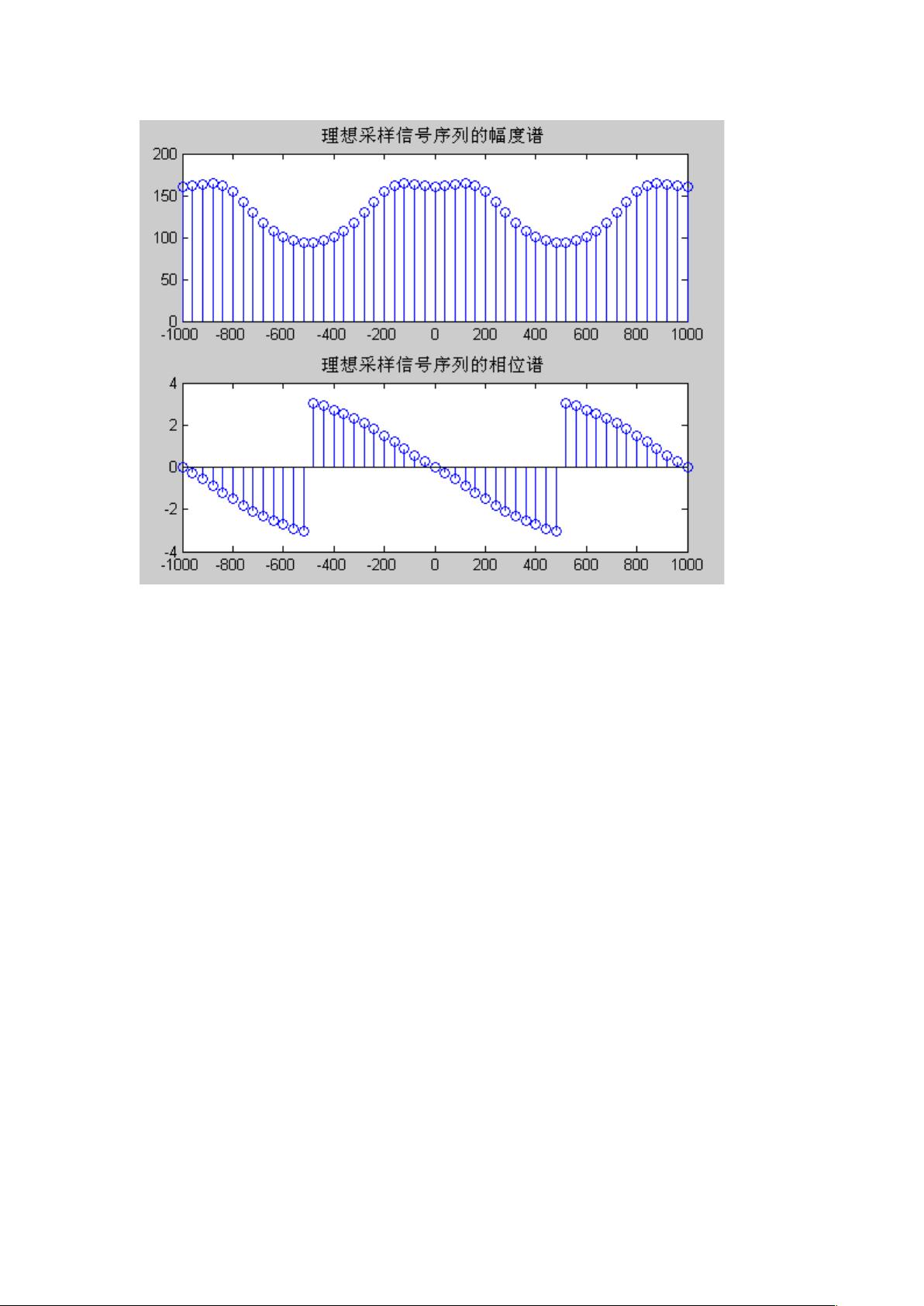
"这个实验主要探讨了数字信号处理中的理想采样信号特性，通过MATLAB程序模拟了不同采样周期(T)下的信号行为。实验中涉及的关键概念包括信号序列、系统响应、幅度谱和相位谱。通过改变采样周期，观察其对信号的影响，从而理解采样定理的重要性。" 在数字信号处理实验中，首先分析了理想采样信号序列的特性。实验采用MATLAB编程环境，通过设置不同的采样周期T来研究信号的变化。例如，当T=1/1000、1/300和1/200时，分别计算和绘制了相应的信号序列。这些步骤旨在揭示采样率对信号质量的影响，特别是在频域中的表现。 实验的第一部分展示了如何生成一个随时间变化的理想采样信号。这里，信号由指数衰减的正弦波组成，其中参数A代表振幅，a是衰减因子，w0是角频率，n是时间样本。MATLAB代码中的`stem`函数用于绘制信号的时间序列，以便直观地查看信号形状。 接下来，实验计算了信号的幅度谱和相位谱，这通过傅里叶变换实现。傅里叶变换是将时域信号转换到频域的关键工具，它能揭示信号的频率成分。在MATLAB中，使用复指数函数对信号进行傅里叶变换，然后计算绝对值（幅度谱）和角度（相位谱）。这些谱图展示了不同采样周期下信号的频域特性，如频率分辨率和失真情况。 通过比较不同采样周期下的幅度谱和相位谱，我们可以观察到采样周期的改变如何影响信号的频谱表示。更小的采样周期意味着更高的采样率，这通常能够更好地保留原始信号的高频信息，但同时也可能增加计算复杂性和存储需求。反之，较大的采样周期可能导致信号的混叠，即高频成分被错误地解释为低频成分，这违反了奈奎斯特定理，可能导致信息丢失或失真。 这个实验提供了一个实践平台，让学生理解和体验数字信号处理的基本概念，特别是理想采样在保持信号完整性和避免混叠方面的作用。通过这样的实验，学习者可以深入理解信号处理理论，并掌握如何用编程工具来分析和可视化信号特性。