MATLAB模拟线性时不变系统：冲激与阶跃响应分析

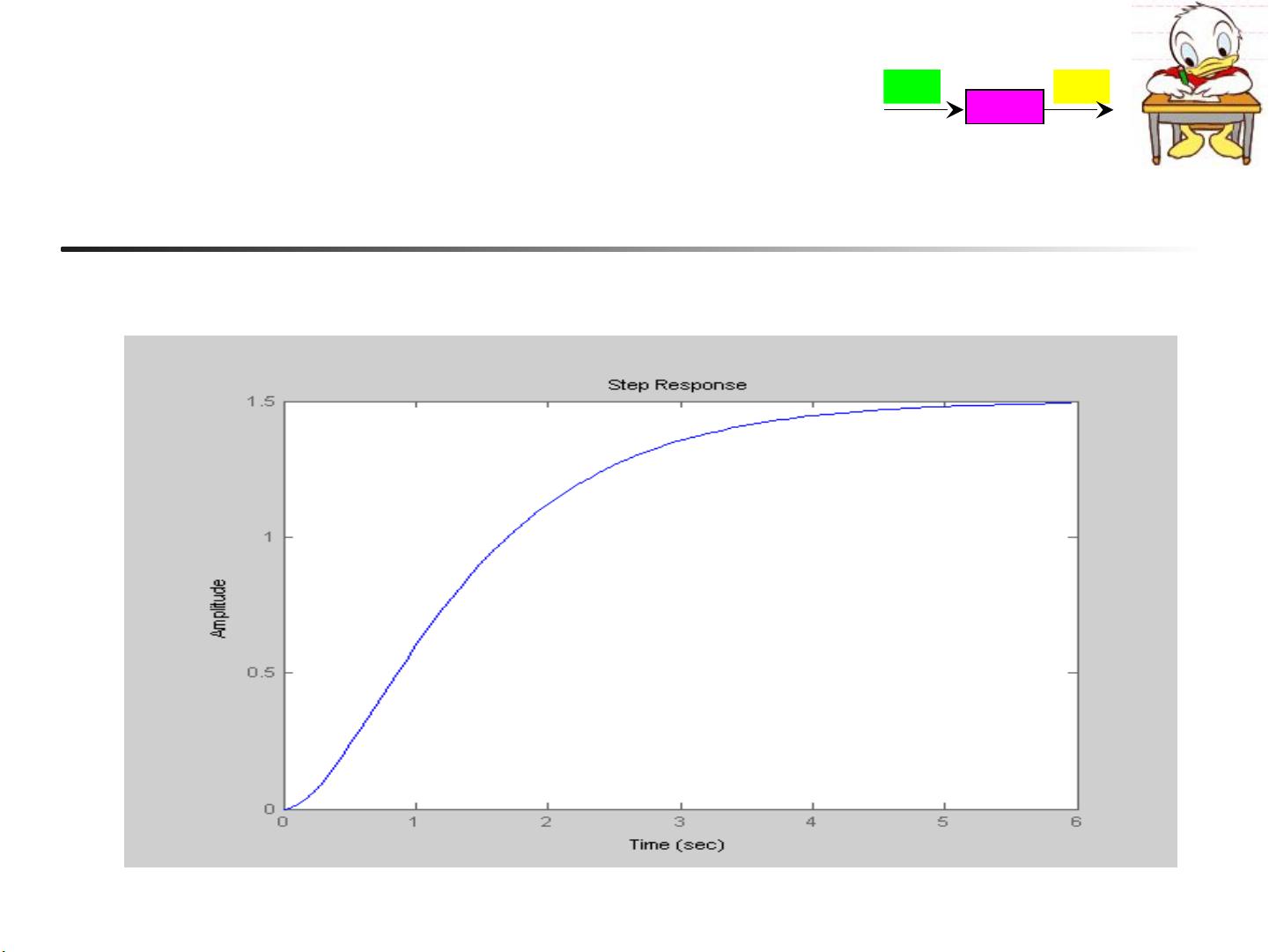
该资源是关于信号与系统的MATLAB实验，主要关注线性时不变（LTI）系统的时域分析。实验内容包括连续和离散系统的冲激响应、阶跃响应、任意激励的零状态响应的计算，以及微分方程的符号解法和卷积的运用。实验通过MATLAB软件进行，提供了如`impulse`、`step`和`lsim`等函数来模拟和分析系统响应。 1. 连续系统的冲激响应h(t)与阶跃响应： 冲激响应是LTI系统对单位冲激函数δ(t)的响应，它完全决定了系统对任何输入信号的响应。在MATLAB中，可以使用`impulse`函数来绘制连续系统的冲激响应波形，例如`impulse(b,a,t1:p:t2)`，其中b和a分别代表系统传递函数的系数，t1、t2和p是时间参数。 2. 阶跃响应g(t)： 阶跃响应是系统对单位阶跃函数的响应，同样可以通过`step`函数来获取和显示，例如`step(b,a,t1:p:t2)`。这个函数用于描绘系统随时间的变化，对于理解和分析系统动态行为非常有用。 3. 任意激励的零状态响应： 对于连续系统，零状态响应(ZSR)是当系统初始状态为零时，系统对任意输入信号的响应。`lsim`函数可以用来模拟ZSR，如`lsim(b,a,x,t)`，其中x是输入信号，t是时间范围。 4. 离散系统的冲激响应h(n)与阶跃响应： 在离散系统中，冲激响应和阶跃响应的概念类似，只是时间变量变为离散的n。MATLAB中的`impulse`和`step`函数也适用于离散系统，不过此时它们处理的是离散时间序列。 5. 微分方程的符号解法： MATLAB可以用于解决线性常微分方程（ODE），这在理解系统的数学模型和特性上很重要。通过符号计算工具箱，可以解析地求解微分方程。 6. 卷积的计算： 卷积是LTI系统理论中的关键运算，用于确定系统响应。在MATLAB中，可以使用`conv`函数来计算连续或离散信号的卷积。 通过这些MATLAB函数和概念，学生可以在实验中深入理解信号处理和系统分析的基本原理，掌握如何运用计算工具来解决实际问题。实验还可能包括线性系统的零极点分析，这有助于识别系统的稳定性和动态特性。这个实验旨在提升学生对信号处理和控制系统理论的实践能力。