非线性有限元分析基础：从理论到实践

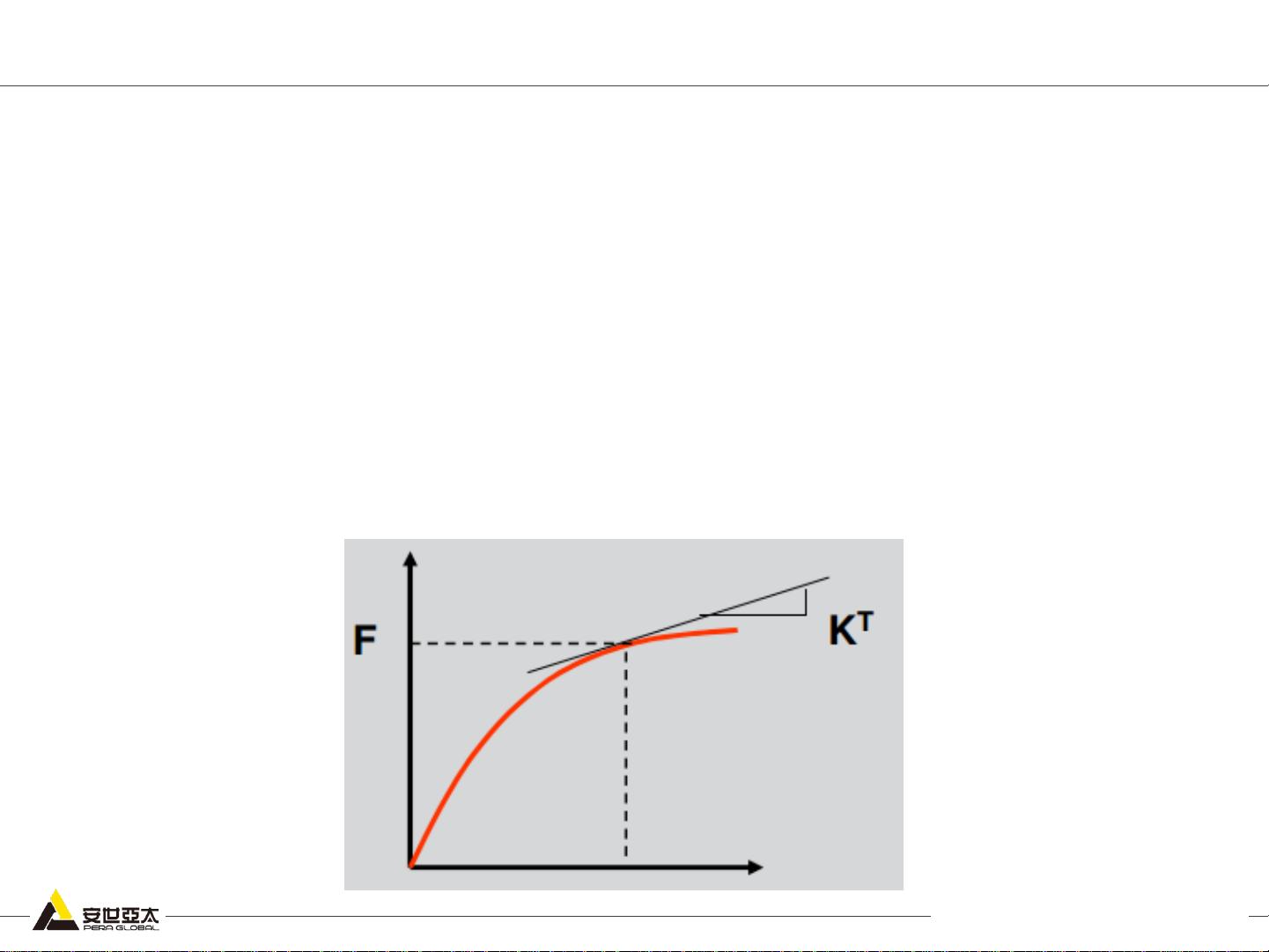
"Mech_SNL_16.0_L01_非线性理论介绍.pdf" 非线性理论在有限元分析中的应用是一个复杂而重要的领域，它涉及到许多实际工程问题的解决方案。本资料主要介绍了非线性有限元分析的基本概念和理论基础，旨在帮助用户理解和掌握非线性结构分析的关键点。 首先，非线性行为是指力和位移之间的关系不再遵循简单的线性关系，即F=Ku，其中F代表力，u代表位移，K为结构的刚度。在线性结构中，刚度是常数，而在线性关系失效时，刚度会随加载路径变化，这种情况下就出现了非线性现象。例如，当结构经历超出弹性范围的应变，或者在大变形情况下（如鱼竿受力弯曲），以及状态改变（如物体间的接触和分离）时，都会出现非线性行为。 非线性行为主要分为三类：几何非线性、材料非线性和接触非线性。几何非线性通常发生在结构变形极大，其几何形状的变化显著影响了结构的行为。材料非线性则涉及到非线性的应力-应变关系，如金属的塑性变形。接触非线性发生在两个物体之间接触状态的改变，例如从分离到接触或反之，这会导致刚度的显著变化。 在处理非线性问题时，尽管问题本身是非线性的，但可以通过线性求解器进行迭代求解。这种方法通过不断逼近真实解来逐步调整载荷步和位移，直到达到收敛标准。非线性有限元分析就是利用这种方法，对这些复杂的非线性问题进行数值模拟，以获得结构在各种工况下的响应。 非线性有限元分析不仅考虑了结构的几何变化，还考虑了材料性质的变化和接触条件的影响。因此，它可以更准确地模拟真实世界中的工程问题，例如桥梁在车辆通行时的挠曲，或是建筑物在地震作用下的动力响应。理解并熟练运用非线性理论对于解决这些复杂问题至关重要，这也是有限元分析在现代工程设计和分析中不可或缺的一部分。 总结来说，非线性理论是有限元分析的一个核心部分，它涵盖了结构变形、材料行为和接触问题的非线性特性。通过非线性有限元方法，我们可以对那些不能简单用线性模型描述的现象进行精确模拟，从而为工程决策提供有力支持。